PINN神经网络求解偏微分方程的11种方法【附论文和代码下载】

如何求解偏微分方程？我们可以将其转化为一个优化问题，先将PDE的信息编码到神经网络的损失函数中，然后使用神经网络来逼近方程的解，这种方法就是基于深度学习的数值方法——PINN。

具体来讲，PINN将偏微分方程表示为一个无限维度的函数空间中的积分方程，然后使用神经网络来逼近这个无限维度的函数空间中的解。在训练过程中，PINN最小化了神经网络的输出与偏微分方程的真值之间的差异，从而学习到了一个可以逼近偏微分方程解的神经网络模型。

相较于传统的数值方法，PINN具有更好的精度和效率，可以处理任意复杂的几何形状和边界条件，而且可以在不需要显式网格的情况下进行计算，有效提高解的准确性和泛化能力。

不过虽然PINN优点很多，目前在这个领域，求解高维PDE时依然会面临一些挑战。今天我就和大家分享一些经典的PINN求解偏微分方程的研究成果，希望可以给同学们提供更多的创新灵感。

论文和代码看文末

1.Physics-informed neural networks：A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations

解决涉及非线性偏微分方程正逆问题的深度学习框架

「简述：」物理信息神经网络是一种用于解决监督学习任务的神经网络，同时遵守由非线性偏微分方程描述的任何给定物理定律。本文介绍了作者在这方面的两个主要问题：数据驱动解决方案和数据驱动发现偏微分方程。作者设计了两种不同类型的算法，即连续时间模型和离散时间模型。通过一系列经典问题，证明了所提出的框架的有效性。

2.Scientifc Machine Learning Through Physics-Informed Neural Networks: Where we are and What's Next

基于物理信息的神经网络的科学机器学习

「简述：」物理信息神经网络（PINN）是一种将偏微分方程编码为神经网络的一种新型方法，用于解决PDE、分数方程、积分-微分方程和随机PDE等问题。本文对PINNs的文献进行了全面综述，介绍了其优势和劣势，并讨论了不同的变体。研究表明，大多数研究都集中在通过不同的激活函数、梯度优化技术、神经网络结构和损失函数结构来定制PINN。尽管PINN已被广泛应用于各种领域，但仍然存在一些理论上的问题需要解决。

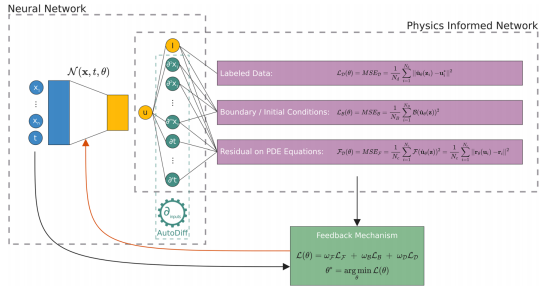
3.DeepXDE: A deep learning library for solving differential equations

用于解决微分方程的深度学习库

「简述：」论文介绍了一种基于深度学习的解决微分方程的方法——物理信息神经网络（PINN）。该方法将偏微分方程嵌入神经网络的损失函数中，并通过自动微分进行求解。作者提出了一种新的基于残差的自适应细化（RAR）方法来提高PINN的训练效率。同时，介绍了一个用于PINN的Python库——DeepXDE，该库可以解决正向问题和反向问题，支持复杂几何域，并具有用户友好性。

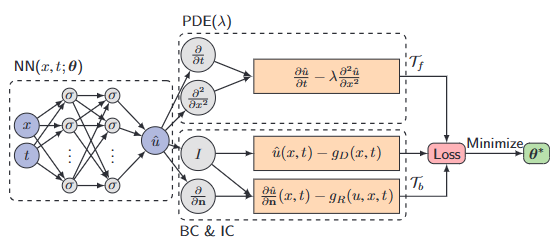
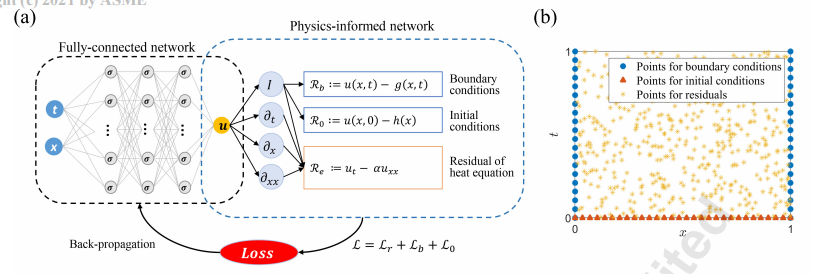
4.Solving partial differential equations using deep learning and physical constraints

使用深度学习和物理约束解决偏微分方程

「简述：」论文介绍了一种改进的物理信息神经网络（PINN）用于解决偏微分方程。PINN将包含在偏微分方程中的物理信息作为正则化项，从而提高神经网络的性能。在本研究中，作者使用该方法研究了波动方程、KdV-Burgers方程和KdV方程。实验结果表明，PINN在解决偏微分方程方面是有效的，值得进一步研究。

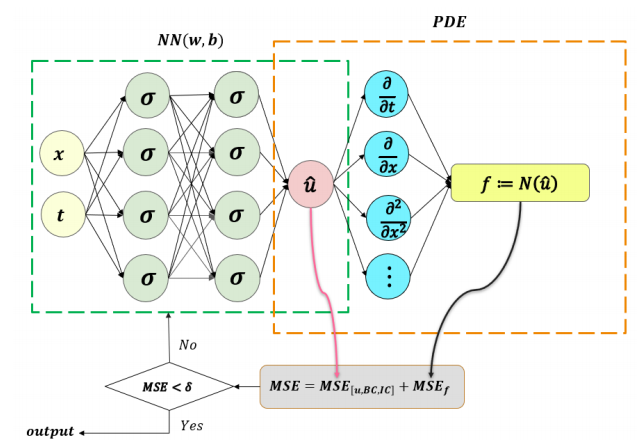
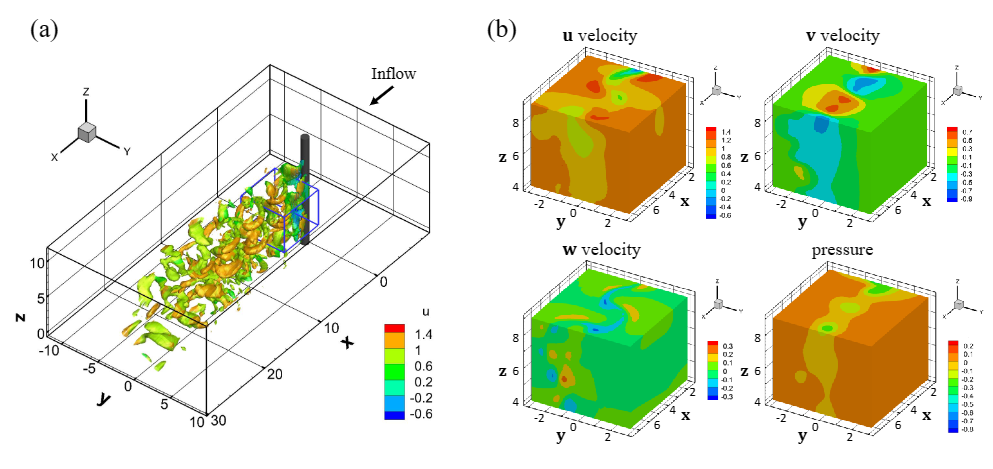
5.Physics-informed neural networks (PINNs) for fluid mechanics: a review

流体力学中的物理信息神经网络（PINNs）

「简述：」论文介绍了使用物理信息神经网络（PINNs）解决流体力学中的流动问题。作者指出，虽然过去50年中已经取得了重大进展，但仍存在一些问题，如无法将噪声数据无缝集成到现有算法中、网格生成复杂、无法处理高维问题等。因此，作者提出了一种整合数据和数学模型的流动物理学感知学习方法，并使用PINNs实现了该方法。实验结果表明，PINNs在与三维尾流、超音速流和生物医学流相关的逆问题方面非常有效。

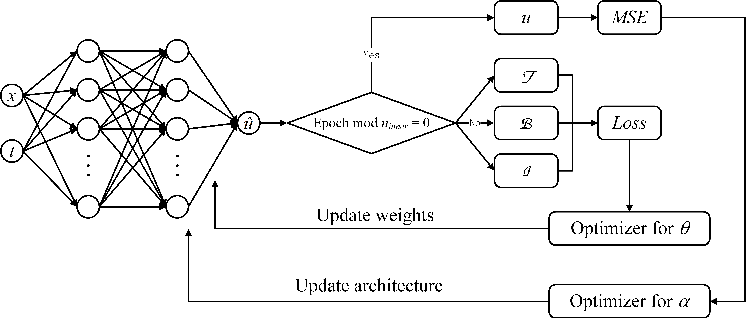
6.NAS-PINN: Neural architecture search-guided physics-informed neural network for solving PDEs

用于求解PDE的神经架构搜索引导的物理信息神经网络

「简述：」论文提出了一种基于神经网络架构搜索的物理信息神经网络（PINN）方法，用于自动搜索解决特定偏微分方程的最优神经网络结构。通过双层优化进行训练，其中内层循环优化神经网络的权重和偏差，外层循环优化体系结构参数。通过数值实验验证了该方法的有效性，并总结了有效解决不同偏微分方程的神经网络结构的特点。研究发现，对于泊松和平流问题，较浅的具有更多神经元的神经网络在PINN中更为合适；对于复杂问题，具有残差连接的神经网络可以提高PINN的性能。

7.A physics-informed neural network technique based on a modifed loss function for computational 2D and 3D solid mechanics

基于改进损失函数的计算2D和3D固体力学的物理信息神经网络技术

「简述：」论文提出了一种改进的损失函数，即最小二乘加权残差（LSWR）损失函数，用于计算二维和三维固体力学的物理信息神经网络（PINN）。该损失函数适用于无量纲形式，仅需要手动确定一个参数。通过数值实验，作者发现基于LSWR损失函数的PINN对于预测位移场和应力场都是有效、鲁棒和准确的。

8.Physics-Informed Neural Networks for Heat Transfer Problems

用于传热问题的物理信息神经网络

「简述：」论文介绍了物理信息神经网络（PINNs）在传热问题中的应用。PINNs能够有效解决真实问题中的有噪声数据和经常部分缺失的物理定律，通过自动微分来评估微分算子，同时定义了一个多任务学习问题，以同时拟合观察到的数据和遵守基本的物理定律。本文针对各种原型传热问题应用了PINNs，特别关注传统计算方法难以处理的真实条件。作者给出了几个具体案例，包括强制对流和混合对流、Stefan问题以及与电力电子学相关的工业应用。结果表明，PINNs可以解决传统计算方法无法处理的问题，并弥合计算和实验传热之间的差距。

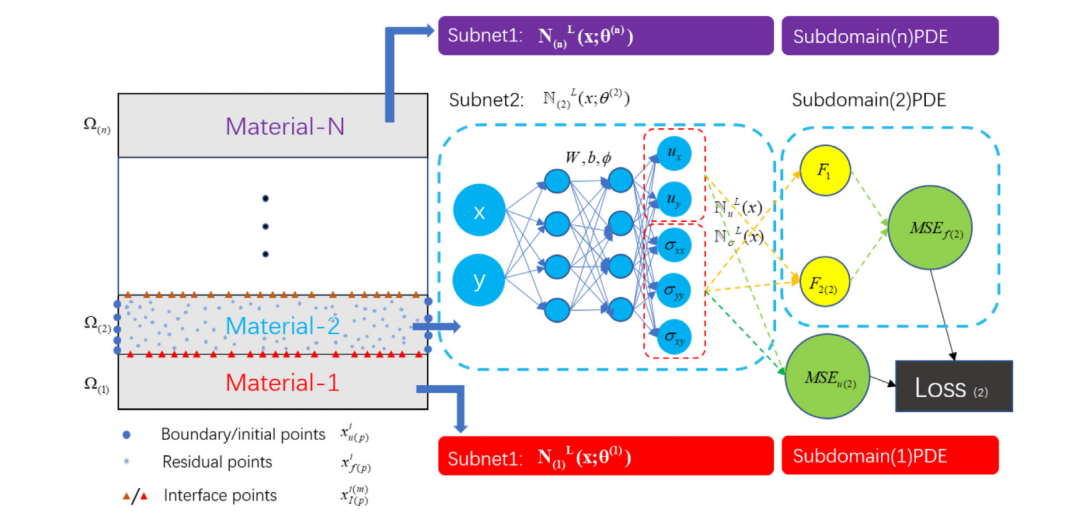
9.Solving multi-material problems in solid mechanics using physics-informed neural networks based on domain decomposition technology

基于域分解技术的物理知识神经网络在固体力学中解决多材料问题

「简述：」本文提出了一种使用物理信息神经网络（PINNs）解决多材料问题的方法。该方法将计算域划分为不同的子网络来表示场变量，并使用额外的正则项描述材料之间的接触关系。通过使用所提出的方法，解决了各种测试案例，包括二维平面应变问题和三维拉伸问题。作者引入了参数共享的概念，并开发了一种具有部分共享结构和全共享模式的网络结构，在解决示例问题时实现了更高的精度。

10.PhyGNNet: Solving spatiotemporal PDEs with Physics-informed Graph Neural Network

使用物理信息图神经网络解决时空偏微分方程

「简述：」论文提出了一种基于图神经网络的物理信息神经网络（PhyGNNet）来解决偏微分方程。该方法将计算区域划分为规则网格，并在网格上定义偏微分算子，然后构建网络优化的PDE损失函数来建立PhyGNNet模型。作者使用Burgers方程和热方程进行比较实验，结果表明该方法在时间和空间方面都具有比PINN更好的拟合能力和外推能力。

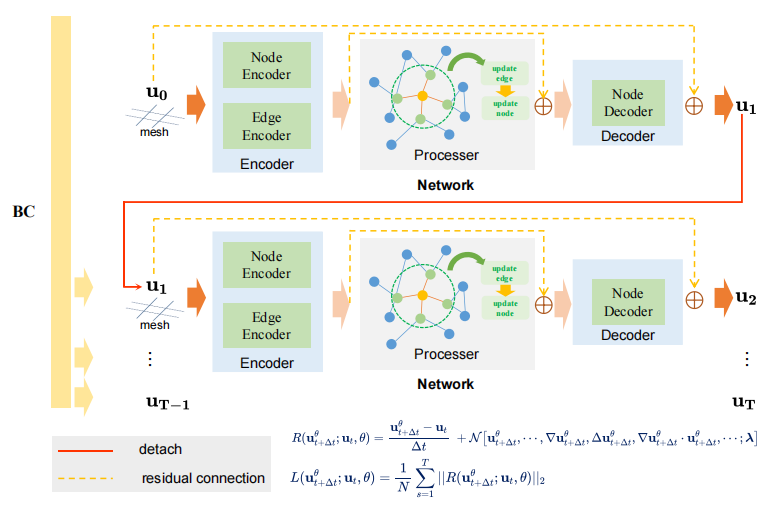
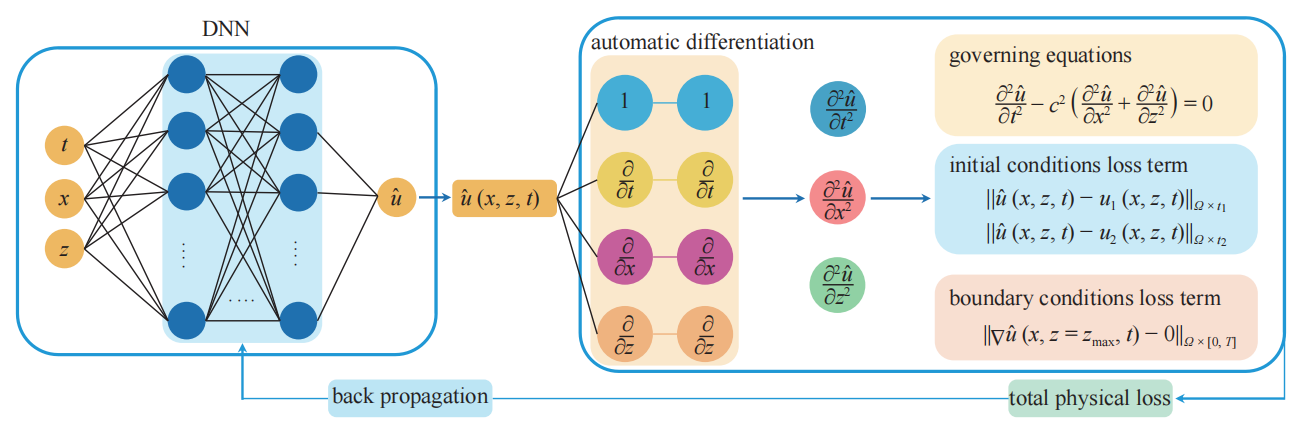
11.Methods and applications of physical information deep learning in wave numerical simulation

物理信息深度学习在波动数值模拟中的方法与应用

「简述：」本文介绍了一种基于物理信息深度学习的方法，用于解决地震工程波动数值模拟中的正演和反问题。通过构建物理信息神经网络（PINN）模型，验证了该方法在解决波动问题中的可行性。同时，采用物理驱动深度学习方法和稀疏的初始波场数据进行二维波动问题的数值模拟，并实现了典型的工作条件。结果表明，物理驱动深度学习方法具有无网格和细粒度数值模拟的优势，并可以实现自由面和边/底边界波场传输等数值模拟条件。

关注下方《学姐带你玩AI》🚀🚀🚀

回复“求解PDE”获取论文+开源代码

码字不易，欢迎大家点赞评论收藏