最小生成树（java版）

📑前言

本文主要是【最小生成树】——最小生成树使用的文章，如果有什么需要改进的地方还请大佬指出??

🎬作者简介：大家好，我是听风与他🥇
??博客首页：CSDN主页听风与他
🌄每日一句：狠狠沉淀，顶峰相见

• 以如下的图为例

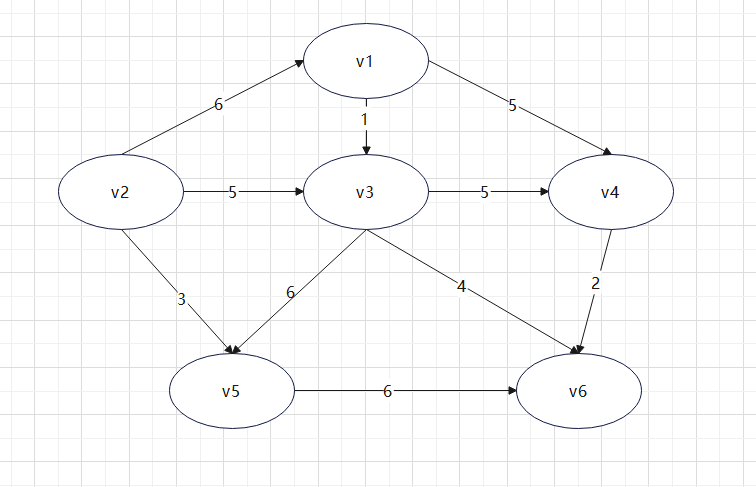
Prime最小生成树

• 按结点来进行遍历

package 图论;

import java.util.Arrays;
import java.util.Scanner;

public class 最小生成树_Prime {
/*
6
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0
 */
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();//顶点个数
		int g[][] = new int[n][n];
		//dis[i]=0; 表示顶点i已经被纳入最小生成树，dis[i]表示最小生成树到顶点i的目前最小距离
		int dis[] = new int[n];//目前最小生成树到其它未访问顶点的最小距离
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				int w = sc.nextInt();//读入矩阵
				if(i==j) g[i][j]=0;//自己到自己距离是0
				else if(w==0) g[i][j]=Integer.MAX_VALUE;//不可达，默认无穷大
				else {
					g[i][j]=w;//否则存储真实的权值
				}
			}
		}
		for(int x[]:g) {
			System.out.println(Arrays.toString(x));
		}
		//prime求最小生成树
		primedo(g, dis, n);
	}
	
	public static void primedo(int[][] g,int[] dis,int n) {
		//最小生成树要包含n个结点，所以这里默认开始Vo结点僵尸最小生成树的第一个结点
		//dis数组存最小生成树到其它未被选择的最小距离0到其它结点的距离
		for(int i=0;i<n;i++) dis[i]=g[0][i];
		dis[0]=0;
		int ans=0;
		for(int i=1;i<n;i++) {//n个结点，最后选择n-1条边，循环就n-1次
			int min=Integer.MAX_VALUE;
			int minindex=-1;//存储最小结点的编号
			for(int j=0;j<n;j++) {
				if(dis[j]<min && dis[j]!=0) {
					min = dis[j];
					minindex=j;//当前j是最小的，未被纳入的顶点编号
				}
			}
			ans=ans+dis[minindex];
			dis[minindex]=0;//把dis[minindex]=0表示minindex结点本轮被纳入最小生成树了
			for(int j=0;j<n;j++) {
				dis[j]=Math.min(dis[j], g[minindex][j]);
			}
		}
		System.out.println(ans);
	}
}

Kruskal最小生成树

• 按边来寻找

package 图论;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;

public class Kruskal {
/*
6 10
0 1 6
0 2 1
0 3 5
1 2 5
1 4 3
2 3 5
2 4 6
2 5 4
3 5 2
4 5 6
 */
	static int[] f;//父亲数组
	
	public static int find(int x) {
		if(f[x]==x) return x;
		else {
			f[x]=find(f[x]);
			return f[x];
		}
	}
	
	public static boolean merge(int a,int b) {
		int f1=find(a);
		int f2=find(b);
		if(f1!=f2) {
			f[f1]=f2;
			return true;//两个顶点来自不同的联通分量
		}
		else return false;//否则形成环，这条边是不合法的
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();//n个顶点，m条边
		int num=0;//表示目前已经采用多少条边
		int sum=0;//最小生成树的边权累加和
		f = new int[n];
		for(int i=0;i<f.length;i++) f[i]=i;//大家属于鼓励联通分量
		ArrayList<edge> list = new ArrayList<edge>();
		for(int i=0;i<m;i++) list.add(new edge(sc.nextInt(), sc.nextInt(), sc.nextInt()));
		Collections.sort(list);
		for(int i=0;i<list.size();i++) System.out.println(list.get(i));
		for(int i=0;i<list.size();i++) {//去检测m条边，不断做合并
			edge check = list.get(i);
			if (merge(check.start,check.end)) {//根据并查集不断的查找两个顶点是否在同一个集合
				System.out.println("采纳"+check);
				sum=sum+check.weight;
				num++;
				if(num==n-1) break;
			}else {
				System.out.println("不采纳");
			}
		}
		System.out.println(sum);
	}

static class edge implements Comparable<edge>{

	int start;
	int end;
	int weight;
	public edge(int s,int e,int w) {
		this.start=s;
		this.end = e;
		this.weight=w;
	}
	@Override
	public int compareTo(edge o) {
		// TODO Auto-generated method stub
		return this.weight-o.weight;
	}
	
	public String toString() {
		return String.format("start=%d\t end=%d\t weight=%d", start,end,weight);
	}
	
}
}

📑文章末尾