力扣hot100 对称二叉树 递归 队列

👨?🏫 题目地址

👨?🏫 参考思路

递归的难点在于：找到可以递归的点 为什么很多人觉得递归一看就会，一写就废。 或者说是自己写无法写出来，关键就是你对递归理解的深不深。

对于此题： 递归的点怎么找？从拿到题的第一时间开始，思路如下：

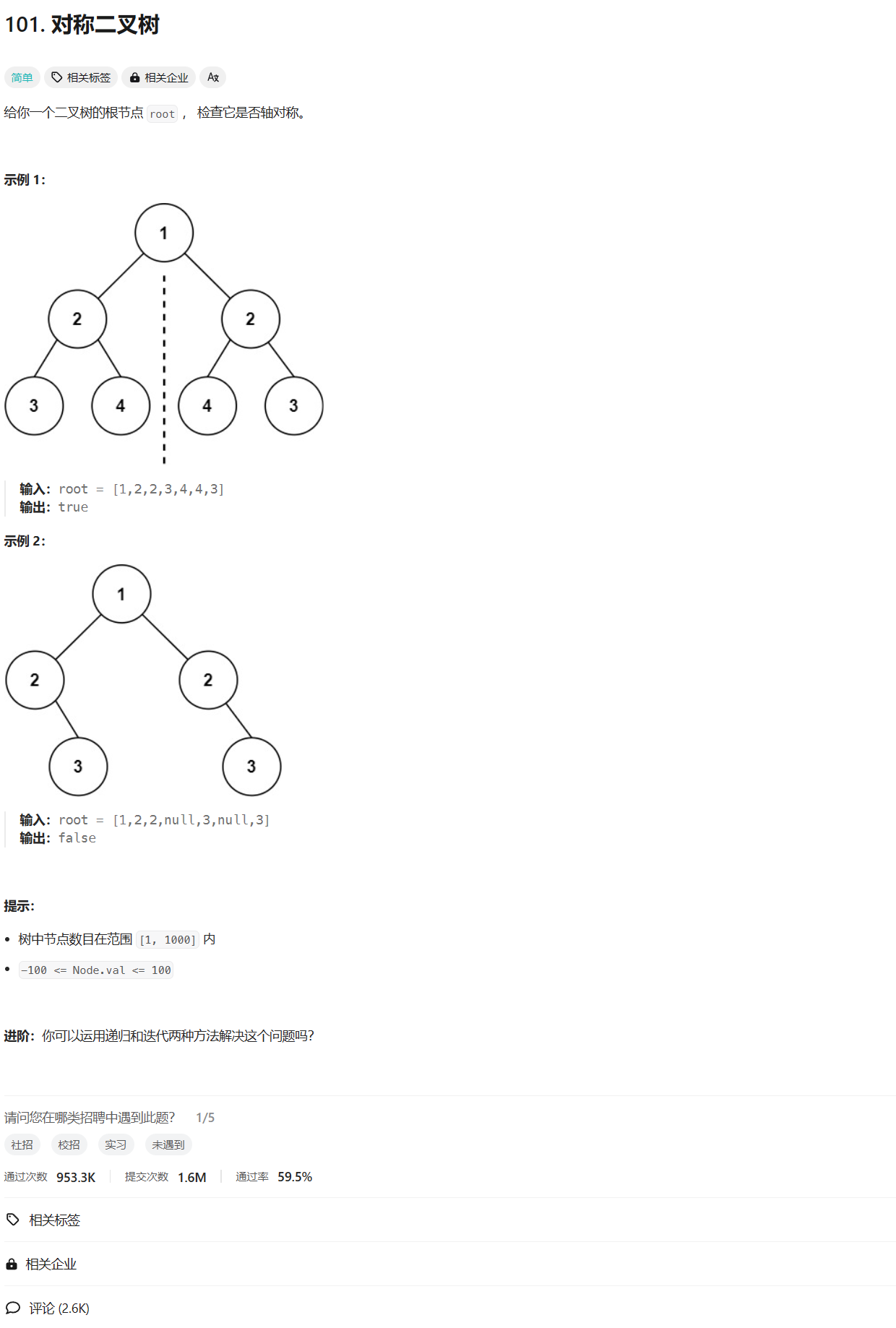
1.怎么判断一棵树是不是对称二叉树？
答案：如果所给根节点，为空，那么是对称。如果不为空的话，当他的左子树与右子树对称时，他对称

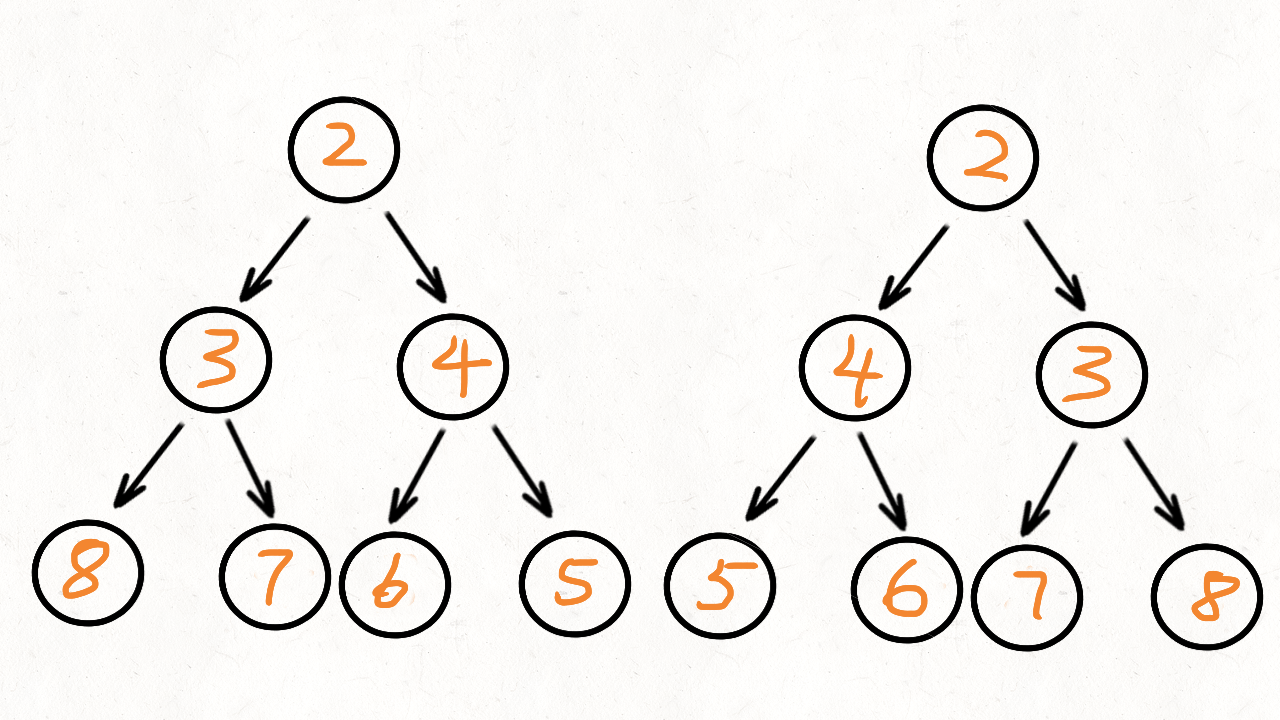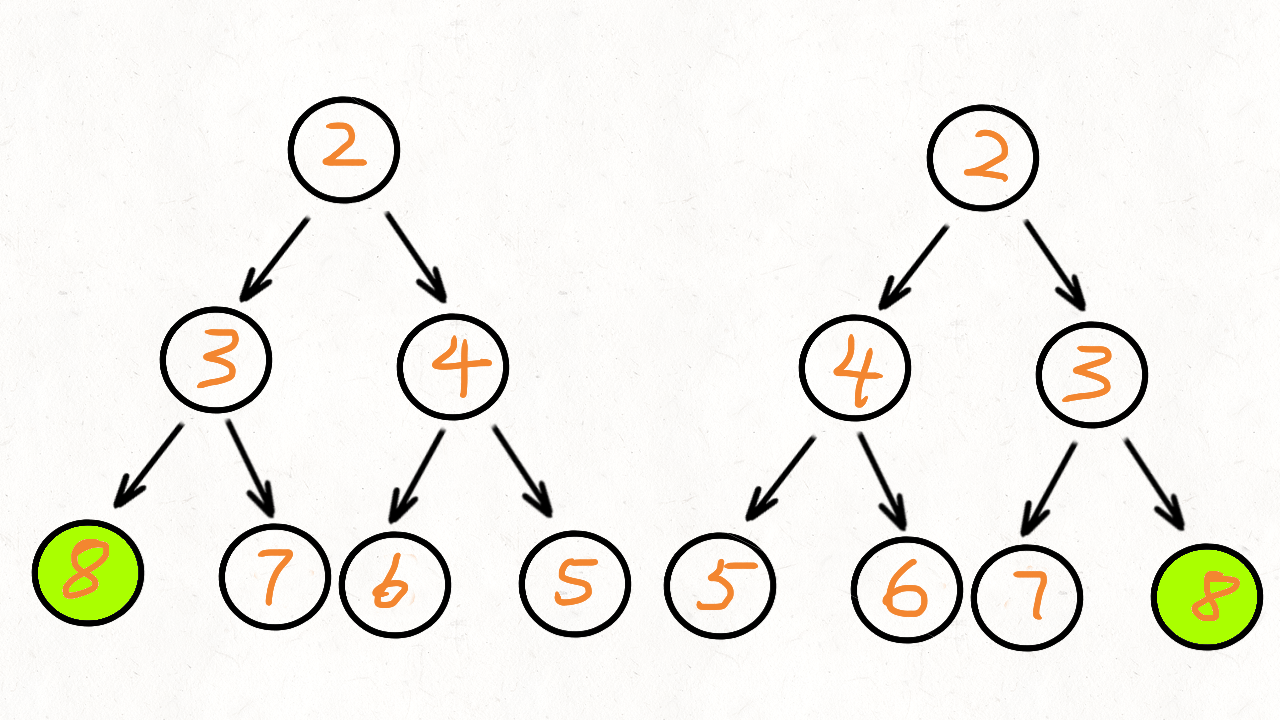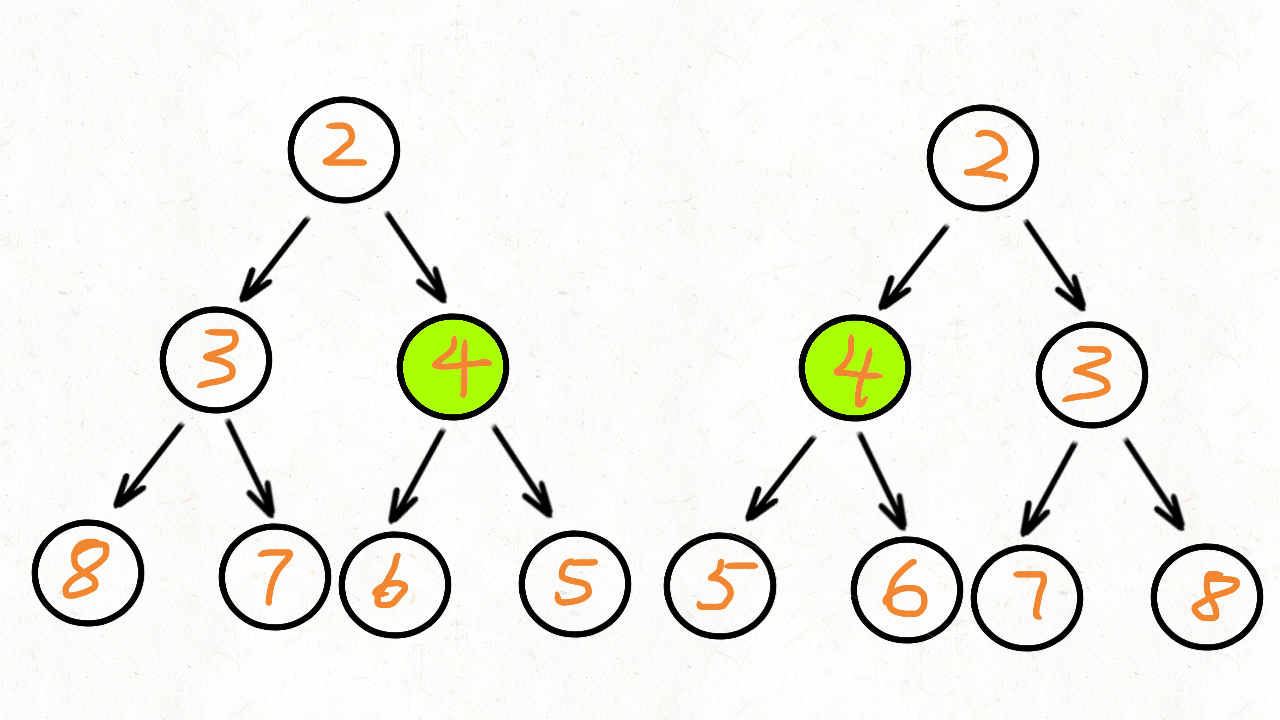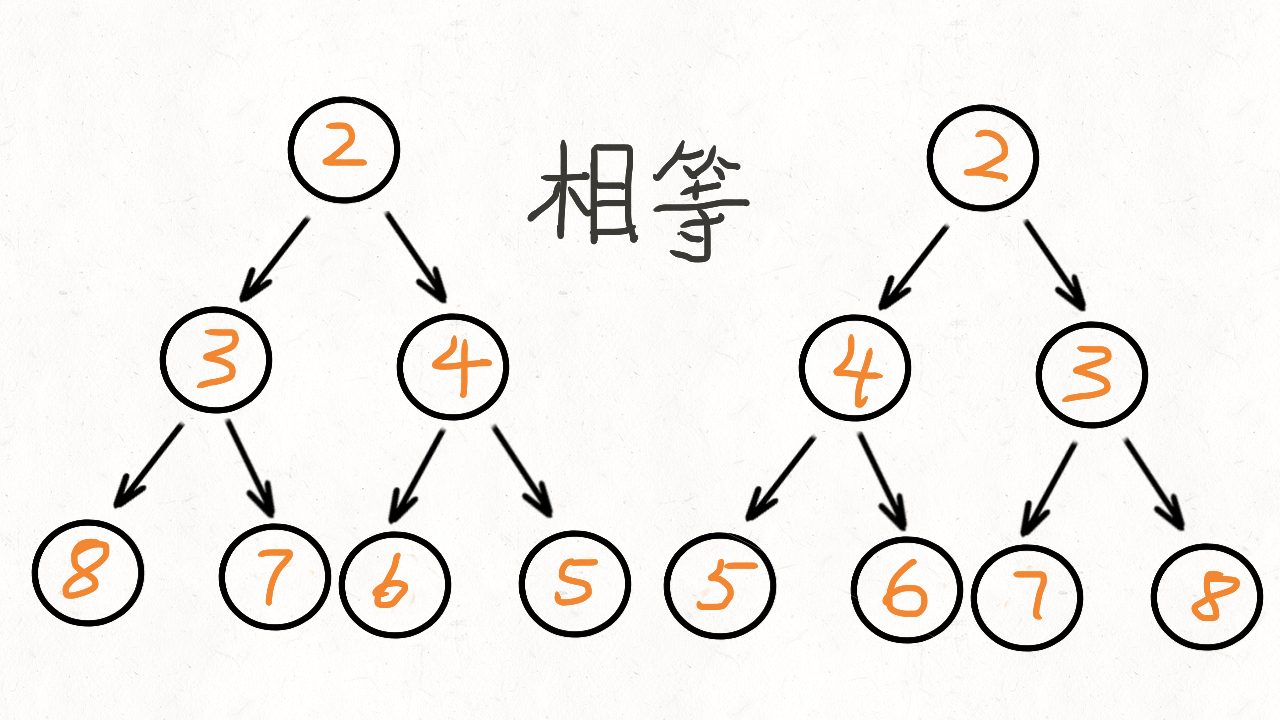
2.那么怎么知道左子树与右子树对不对称呢？在这我直接叫为左树和右树
答案：如果左树的左孩子与右树的右孩子对称，左树的右孩子与右树的左孩子对称，那么这个左树和右树就对称。

仔细读这句话，是不是有点绕？怎么感觉有一个功能A我想实现，但我去实现A的时候又要用到A实现后的功能呢？

当你思考到这里的时候，递归点已经出现了： 递归点：我在尝试判断左树与右树对称的条件时，发现其跟两树的孩子的对称情况有关系。

想到这里，你不必有太多疑问，上手去按思路写代码，函数A（左树，右树）功能是返回是否对称

def 函数A（左树，右树）： 左树节点值等于右树节点值 且 函数A（左树的左子树，右树的右子树），函数A（左树的右子树，右树的左子树）均为真 才返回真

实现完毕

写着写着，你就发现你写出来了。

👨?🏫 参考题解

😋 递归实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    	public boolean isSymmetric(TreeNode root)
	{
		return isSame(root.left, root.right);
	}

	private boolean isSame(TreeNode l, TreeNode r)
	{
		if (l == null || r == null)// 只要 l 和 r 中有一个 null 的，则说明不对称；l 和 r 都为空 即递归出口
			return l == r;

		return l.val == r.val && isSame(l.left, r.right) && isSame(l.right, r.left);
	}
}

😋 队列实现

class Solution {
	public boolean isSymmetric(TreeNode root) {
		if(root==null || (root.left==null && root.right==null)) {
			return true;
		}
		//用队列保存节点
		LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
		//将根节点的左右孩子放到队列中
		queue.add(root.left);
		queue.add(root.right);
		while(queue.size()>0) {
			//从队列中取出两个节点，再比较这两个节点
			TreeNode left = queue.removeFirst();
			TreeNode right = queue.removeFirst();
			//如果两个节点都为空就继续循环，两者有一个为空就返回false
			if(left==null && right==null) {
				continue;
			}
			if(left==null || right==null) {
				return false;
			}
			if(left.val!=right.val) {
				return false;
			}
			//将左节点的左孩子， 右节点的右孩子放入队列
			queue.add(left.left);
			queue.add(right.right);
			//将左节点的右孩子，右节点的左孩子放入队列
			queue.add(left.right);
			queue.add(right.left);
		}
		
		return true;
	}
}