excel统计分析——偏度、峰度

发布时间：2023年12月21日

参考链接：

偏度与峰度的正态性分布判断 - 知乎

描述统计学 - 知乎

样本偏度(skewness)与随机变量的偏度及三阶统计量之间的关系和计算估计-CSDN博客

数据分析中如何衡量数据的分布 - 知乎

KURT 函数 - Microsoft 支持

SKEW 函数 - Microsoft 支持

Standard errors of skewness and kurtosis are all the same for a set of variables

用偏度系数、峰度系数考察正态性假设 - 知乎

1、偏度

? ? ? ? 偏度衡量随机变量概率分布的不对称性，是相对于平均值不对称程度的度量，通过对偏度系数的测量，我们能够判定数据分布的不对称程度以及方向。
? ? ? ?具体来说，对于随机变量X，我们定义偏度为其的三阶标准中心距。我们可以基于矩估计，得到总体的偏度为:

SK=\frac{m_{3}}{m_{2}^{3/2}}=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{3}}{[\frac{1}{n}\sum_{n=1}^{n}(x_{i}-\bar{x})^{2}]^{\frac{3}{2}}}

其中，\bar{x}为总体均值，m_{3}为三阶中心距，m_{2}为二阶中心距。

样本量为n的样本偏度，可表示为：

SK=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{3}}{[\frac{1}{n-1}\sum_{n=1}^{n}(x_{i}-\bar{x})^{2}]^{\frac{3}{2}}}

而在许多文献中，尤其对小样本来说，一个常用的样本偏度的估计，计算公式为：

? ? ? ??SK=\frac{n^{2}}{(n-1)(n-2)}\frac{m_{3}}{s^{3}}=\frac{n^{2}}{(n-1)(n-2)}\times \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{3}}{[\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}]^{\frac{3}{2}}}

? ? ? ?偏度的衡量是相对于正态分布来说，正态分布的偏度为0，即若数据分布是对称的，偏度为0。若偏度大于0，则分布右偏，即分布有一条长尾在右；若偏度小于0，则分布为左偏，即分布有一条长尾在左（如下图）；同时偏度的绝对值越大，说明分布的偏移程度越严重。【注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置。】

2、峰度

? ? ? ? 峰度，是研究数据分布陡峭或者平滑的统计量，通过对峰度系数的测量，我们能够判定数据相对于正态分布而言是更陡峭还是更平缓。比如正态分布的峰度为0，均匀分布的峰度为-1.2（平缓），指数分布的峰度6（陡峭）。

峰度定义为四阶中心距除以方差的平方减3（这也被称为超值峰度，“减3”是为了让正态分布的峰度为0），总体的超值峰度公式可表示为：

K=\frac{m_{4}}{m_{2}^{2}}-3=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{4}}{(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^2)^{2}}-3

样本为n的样本峰度，可表示为：

K=\frac{n(n+1)(n-1)}{(n-2)(n-3)}\times \frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{4}}{(\sum_{i=1}^{n}(x_{i}-\bar{x})^{2})^{2}}-\frac{3(n-1)^{2}}{(n-2)(n-3)} =\frac{n^{2}(n+1)}{(n-1)(n-2)(n-3)}\times \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{4}}{(\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2})^{2}}-\frac{3(n-1)^{2}}{(n-2)(n-3)}

? ? ? ? 若峰度?≈?0 , 分布的峰态服从正态分布；
? ? ? ? 若峰度>0,分布的峰态陡峭（高尖）；
? ? ? ? 若峰度<0,分布的峰态平缓（矮胖）。

3、正态性判断

? ? ? ? 对于一组数据来说，如果计算出来的偏度和峰度都在0附近，那么可以初步判断其分布服从正态分布。

? ? ? 我们可以把偏度系数和峰度系数转换为标准正态分布的Z值。转换为Z值后:

  1. 可以比较不同样本的不同单位数据的偏度系数和峰度系数。
  2. 可以根据Z值表计算出如果数据符合分布，出现目前样本偏度系数/峰度系数或更极端值的可能性大小，即可以对偏度系数或者峰度系数是否为0做假设检验。

? ? ? ? 将某统计量转换为标准正态分布Z值，只需要将该统计量减去该统计量分布的均值后再除以该统计量的标准差（标准误）就行了。这里我们假设检验中原假设是系数为0，所以减去的均值用0来带入。标准正态分布下双侧尾部面积0.05对应Z值为1.96。因此转换后的Z值如果绝对值大于1.96（也可以将其近似为2），对应P值就小于0.05。

? ? ? ? 应用时需要注意：大样本量下标准误会较小，即使系数距离0很近得到的Z值也会很大，容易拒绝原假设。当样本量小于100时，尝试峰度和偏度系数来判断样本的正态性会比较合理。当样本量大于100时，这种显著性检验意义就不大了（因为即使很小的差异也很容易有统计学意义），更需要结合作图观察数据分布的形状。

Z值转换步骤如下：

Z=|K-0|/SK （K为偏度，SK为偏度的标准误）

其中，SK=\sqrt{\frac{6\times N\times (N-1)}{(N-2)\times (N+1)\times (N+3)}}，N为样本量。

? ? ? ??

Z=|S-0|/SS （S为峰度，SS为峰度的标准误）

其中，SS=\sqrt{\frac{4\times (N^{2}-1)\times SK^{2}}{(N-3)(N+5)}}，N为样本量，SK为样本偏度的标准误

? ? ? ? 在α=0.05的情况下，Z值绝对值大于1.96时，即可认为K系数或S系数显著不等于0，即样本数据非正态。

4、excel操作步骤

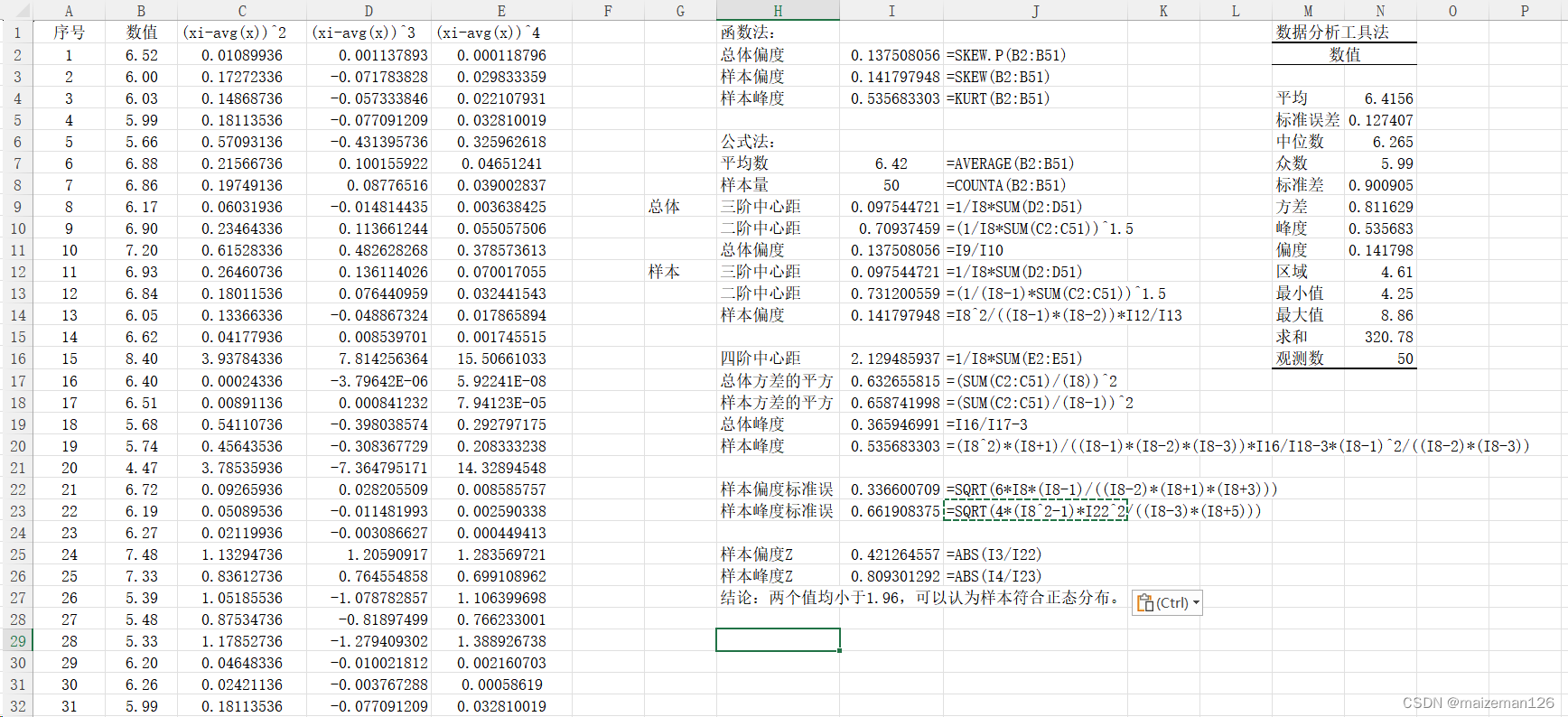
文章来源:https://blog.csdn.net/maizeman126/article/details/135127573
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章