# C++系列-第3章循环结构-28-累加

在线练习：
http://noi.openjudge.cn/
https://www.luogu.com.cn/

累加

奥运奖牌计数

题目描述

$2008$ 年北京奥运会，A 国的运动员参与了 $n$ 天的决赛项目 $(1\le n\le 100)$。现在要统计一下 A 国所获得的金、银、铜牌数目及总奖牌数。输入第 $1$ 行是 A 国参与决赛项目的天数 $n$，其后 $n$ 行，每一行是该国某一天获得的金、银、铜牌数目（不超过 $100)$。输出 $4$ 个整数，为 A 国所获得的金、银、铜牌总数及总奖牌数。

输入格式

第 $1$ 行是 A 国参与决赛项目的天数 $n$，其后 $n$ 行，每一行是该国某一天获得的金、银、铜牌数目，以一个空格分开。

输出格式

输出 $1$ 行，包括 $4$ 个整数，为 A 国所获得的金、银、铜牌总数及总奖牌数，以一个空格分开。

样例 #1

样例输入 #1

3
1 0 3
3 1 0
0 3 0

样例输出 #1

4 4 3 11

代码实现

#include<iostream>
using namespace std;
int main()
{
	/*
	3
1 0 3
3 1 0
0 3 0
	*/
   int a,c,d,b,e=0,f=0,g=0;//e,f,g分别是金银铜牌总数,a为天数
   cin>>a;
   for(int i=0;i<a;++i)
   {
       cin>>c>>d>>b;//输入：金银铜牌数量
       e+=c;
       f+=d;
       g+=b;
    }
    cout<<e<<' '<<f<<' '<<g<<' '<<e+f+g;//金、银、铜牌总数及总奖牌数
    return 0;
}

输出为：

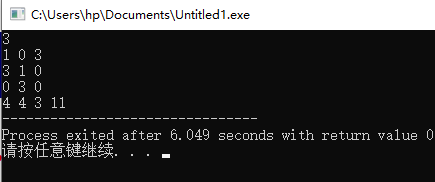
数列分段

[题目描述]

对于给定的一个长度为 n 的正整数数列a;，现要将其分成连续的若干段并且每段和不超过 m(可以等于 m)，问最少能将其分成多少段使得满足要求

[输入]

第一行包含两个正整数 n,m，表示了数列的长度与每段和的最值
第二行包含n个空格隔开的非负整数ai。
数据范围:1<n<105 1<=ai<=m<=104。

[输出格式]

输一个正整数，输出最少划分的段数。

[样例输入]

5 6
4 2 4 5 1

[样例输出]

3

代码

#include<iostream>
using namespace std;
int n,m,a,sum,cnt;
int main()
{
	/*
5 6
4 2 4 5 1
	*/
   cin>>n>>m;
   for(int i=1;i<n;i++)
   {
   	   cin>>a;
   	   if(sum+a>m){
   	   	    cnt++;
   	   	    sum=a;
		}
       else sum+=a;
    }
    cout<<cnt+1;
    return 0;
}

输出为：

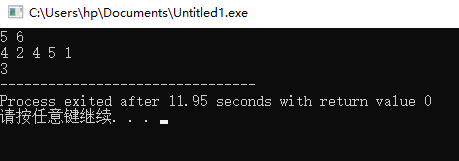
短信计费

[题日描述]

用手机发短信，一条短信资费为0.1 元，但限定一条短信的内容在 70个字以内(包括 70 个字)。如果一次所发送的短信超过了 70 个字，则会按照每 70个字一条短信的限制把它分割成多条短信发送。假设已经知道某人当月所发送的短信的字数，试统计一下他当月短信的总资费

[输入格式]

第一行是整数 n(1 <n100)，表示当月发送短信的总次数，接着 n 行每行一个整数(不超过 1000)，表示每次短信的字数。

[输出格式]

输出一行，当月短信总资费，单位为元，精确到小数点后 1 位

样例输入

10
39
49
42
61
44
147
42
72
35
46

样例输出

1.3

代码

#include<iostream>
using namespace std;
double ans;
int n,x;
int main()
{
	/*

	*/
   cin>>n;
   for(int i=1;i<=n;i++)
   {
   	    cin>>x;
   	    int y=x/70; //y为x个70字 
   	    if(x%70) y++; // 如果x不是70的整数倍 执行y++ 
   	    ans += y*0.1;
    }
    printf("%.1lf",ans);
    return 0;
}

输出为：

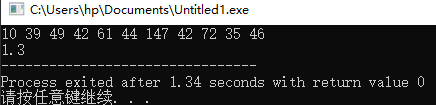
什么是e

e是增长极限

你不会自成“大款”——到e为止

e与复利

e与飞蛾扑火

令人惊奇的是，它还藏身于古人口口相传的故事里。古人常用“飞蛾扑火”来表达对一部分人自不量力的藐视，也用它来称颂为了爱情而视死如归的恋人。然而，飞蛾扑火的悲剧里也伫立着e的背影。人类对这一现象理解的常见误区，是认为昆虫具有趋光性，因此就容易被火光所吸引，从而自取灭亡。通过对昆虫习性的长期研究，人们才发现，飞蛾扑火仅仅是因为它认为自己是在以正确的路线飞行，而不知道早已深处险境。

原来，夜晚活动的昆虫为了确保自己的运动方向，通常以月光作为参考。它在漫长的进化中，已经学会了让自己的行动路线和一束平行光线保持固定的角度，这样就能以直线飞行。

月亮与地球的距离过于遥远，每一束到达地球的月光都可以近似看做平行线。虫子就是靠着这亿万年来皎洁的月光为自己导航。不幸的是，当灯光出现以后，它的亮度远远超过月光时，灯光周围的虫子就会把这个最强的光源作为指引它飞行的灯塔。这就为悲剧埋下了种子。

由于每一缕灯光都是从一点发出来，在周围空间呈现辐射状。飞蛾根据进化的习惯，依然保持跟每一缕光线相同的夹角飞行。最后的结果，就是旋转地一圈一圈坠入灯光的中心。飞蛾的飞行曲线被称为斐波拉契螺旋线。它描述的就是一个在辐射状的网格图里，按照和每条辐射线保持固定夹角的曲线模型。

$p(t)=e^t$公式

位置由e的t次方来描述
t是时间。

e与彩票一次不中

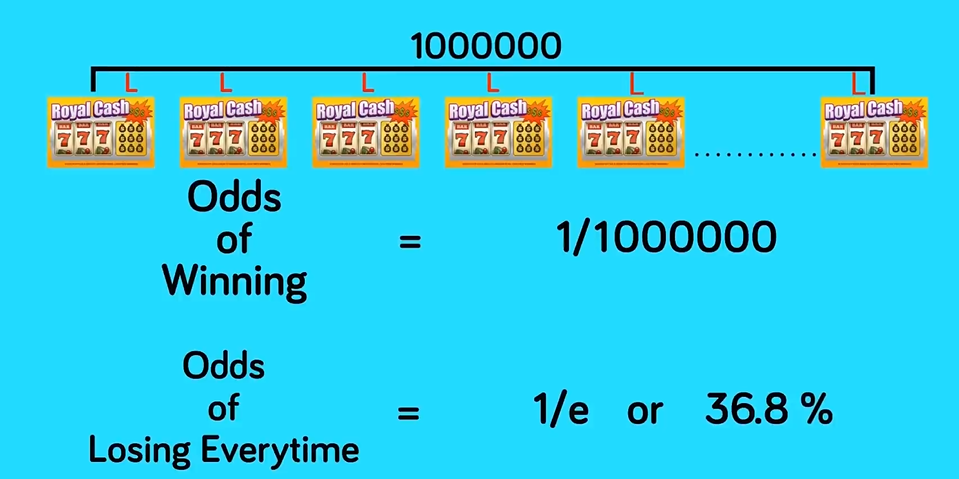
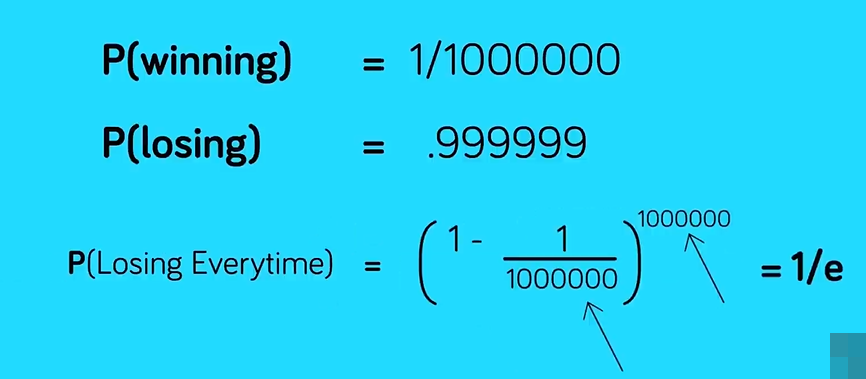
e与随机拿伞

e与牌的随机洗牌

e与聘请人员

e与分绳子

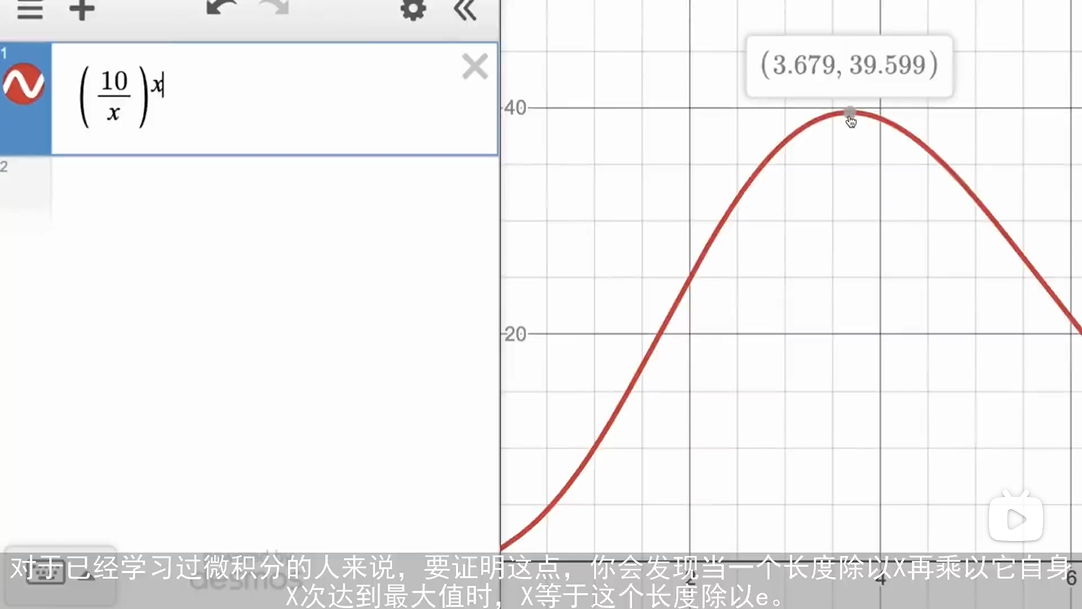
e与普特南考试

37%与e

求出 e 的值

题目描述

利用公式 $e=1+1/1!+1/2!+1/3!+?+1/n!$，求 $e$ 的值，要求保留小数点后 $10$ 位。

输入格式

输入只有一行，该行包含一个整数 $n$，表示计算 $e$ 时累加到 $1/n!$。

输出格式

输出只有一行，该行包含计算出来的 $e$ 的值，要求打印小数点后 $10$ 位。

样例 #1

样例输入 #1

10

样例输出 #1

2.7182818011

提示

$2\le n\le 15$。

代码

#include<iostream>
#include<stdio.h>
using namespace std;
int main()
{
	int n;
	double e=1.0,sum=1.0;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		e*=i;
		sum+=1/e;
	}
	printf("%0.10lf",sum);
	return 0;
}

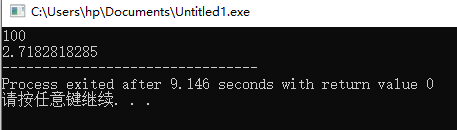
输出为：

总结

本文是C++系列博客，主要讲述常数e和累计的计算