牛客周赛 Round 13 解题报告 | 珂学家 | 乘法原理场 + BFS上组合 + 众数贪心

---

前言

---

整体评价

终于回归了周赛的5题制，还是喜欢这种。题目有难度，才会有进度。

D是道很特别的题，感觉很典，它是基于BFS基础上的乘法组合, E也是道好题，模拟贪心好像是错的，得从众数的角度去剖析。

---

A. 矩阵转置置

模拟即可

import java.io.*;
import java.util.*;
import java.util.stream.*;

public class Main {

    public static void main(String[] args) {
        
        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        int n = sc.nextInt();
        int[][] arr = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                arr[i][j] = sc.nextInt();
            }
        }

        // 上下整体置换
        for (int i = 0, j = n - 1; i < j; i++, j--) {
            for (int k = 0; k < n; k++) {
                // swap
                int t = arr[i][k];
                arr[i][k] = arr[j][k];
                arr[j][k] = t;
            }
        }

        // 左后整体置换
        for (int i = 0, j = n - 1; i < j; i++, j--) {
            for (int k = 0; k < n; k++) {
                // swap
                int t = arr[k][i];
                arr[k][i] = arr[k][j];
                arr[k][j] = t;
            }
        }

        for (int i = 0; i < n; i++) {
            System.out.println(
                    Arrays.stream(arr[i]).mapToObj(String::valueOf)
                            .collect(Collectors.joining(" "))
            );
        }
    }

}

---

B. 小红买基金

设满足条件的基金m

每一个可选/不选

但至少有一个基金存在

最后为 $2^m?1$

import java.io.BufferedInputStream;
import java.util.Scanner;

public class B1 {

    static long ksm(long b, long v, long mod) {
        long r = 1l;
        while (v > 0) {
            if (v % 2 == 1) {
                r = r * b % mod;
            }
            b = b * b % mod;
            v /= 2;
        }
        return r;
    }

    public static void main(String[] args) {

        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        int n = sc.nextInt(), x = sc.nextInt(), y = sc.nextInt();

        int m = 0;
        for (int i = 0; i < n; i++) {
            int u = sc.nextInt(), v = sc.nextInt();
            if (u >= x && v <= y) {
                m++;
            }
        }

        long mod = (long)1e9 + 7;
        long r = ksm(2, m, mod);

        r = ((r - 1) % mod + mod) % mod;

        System.out.println(r);
        
    }

}

---

C. 小红的密码修改

分类计数的题

对这几个类别进行统计，然后枚举计算

不过需要分类讨论

• 如果某一类有且仅有一个元素, 那只能在该类中变化
• 如果某一类超过一个元素，那可以在全范围内进行变化
  注: 不能变成自己

import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {

    static int[] parse(char[] str) {
        int[] res = new int[4];
        for (char c: str) {
            if (c >= 'a' && c <= 'z') res[0]++;
            else if (c >= 'A' && c <= 'Z') res[1]++;
            else if (c >= '0' && c <= '9') res[2]++;
            else if (",.?!".indexOf(c) != -1) res[3]++;
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int t = sc.nextInt();
        while (t-- > 0) {
            char[] str = sc.next().toCharArray();
            // 分类统计
            int[] hash = parse(str);

            long r = 0;
            for (int i = 0; i < hash.length; i++) {
                if (hash[i] == 1) {
                    if (i == 0) r += (26 - 1);
                    else if (i == 1) r += (26 - 1);
                    else if (i == 2) r += (10 - 1);
                    else if (i == 3) r += (4 - 1);
                } else {
                    r += (long)hash[i] * (26 + 26 + 10 + 4 - 1);
                }
            }
            System.out.println(r);
        }

    }

}

---

D. 小红的转账设置方式

这题分两部

• 最短路计算

• 计算总方案数

求最小总代价，这个BFS最短路就可以出来

难点在于: 总方案数

这个方案总数和边的方向有关

在保证最小代价不变的情况下，也就是保证每个点的最小路径不变(有向图）

可以观察到

1. 图存在两种类型的边

• 参与最短路的边
• 没有参与最短路的边

2. 如何处理参与最短路的边

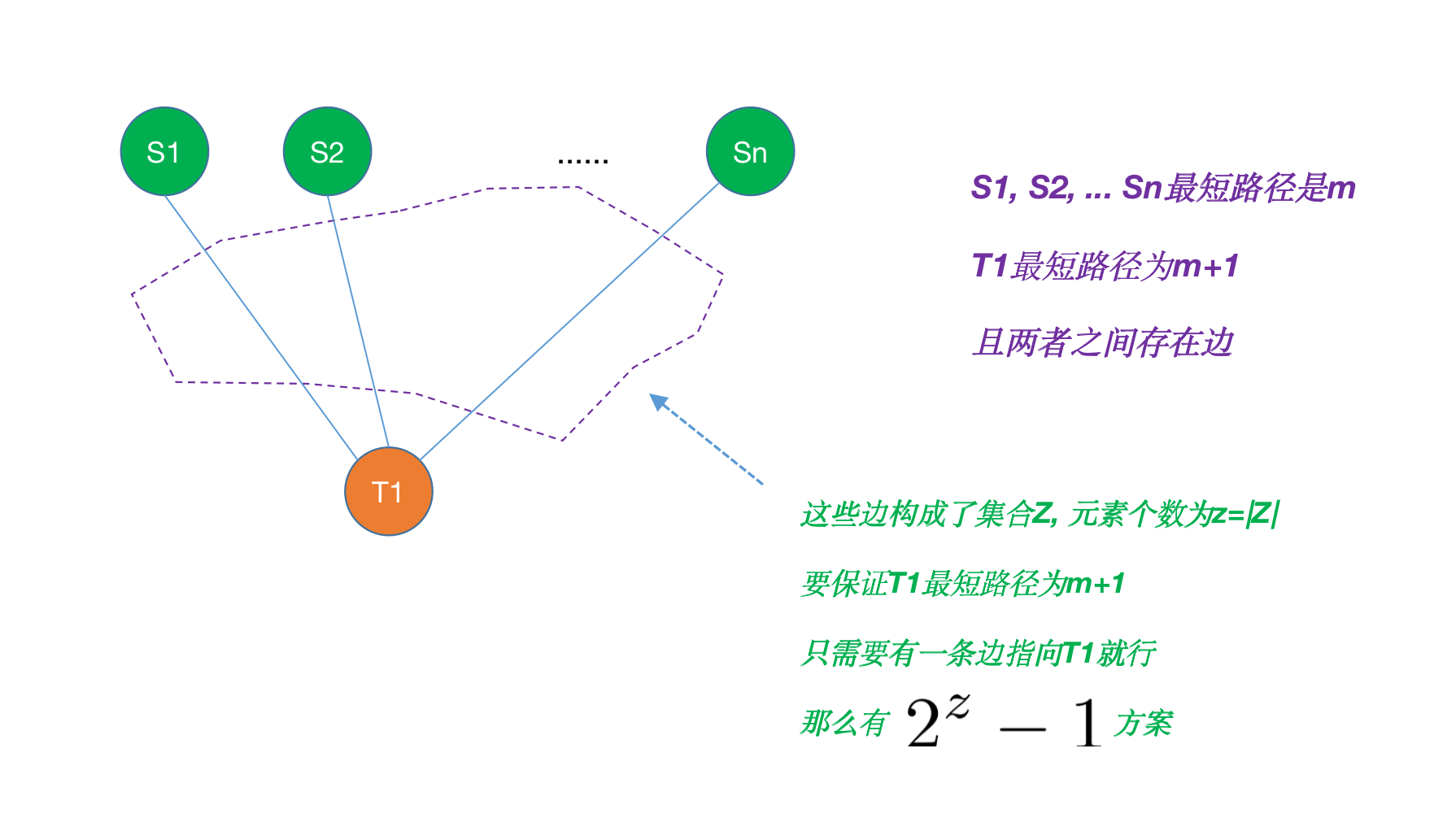
参与最短路的边，实际上 仅 属于一个集合，由集合贡献 $2^z?1$

3. 如何处理非参与最短路的边

这类边，正反都可以，不影响结果，贡献2

---

分析到这里，这题的解题思路就很容易了。

• 先BFS预处理所有的点(最短路）
• 从点出发，找到上游的点集(边集), 贡献$2^z?1$
• 找到剩下的非参与最短路的点集, 贡献2
• 乘法原理

import java.io.*;
import java.util.*;

public class Main {

    static long ksm(long b, long v, long mod) {
        long r = 1l;
        while (v > 0) {
            if (v % 2 == 1) {
                r = r * b % mod;
            }
            b = b * b % mod;
            v /= 2;
        }
        return r;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        int n = sc.nextInt(), m = sc.nextInt();

        List<Integer>[]g = new List[n + 1];
        Arrays.setAll(g, x -> new ArrayList<>());

        int[][] edges = new int[m][2];
        for (int i = 0; i < m; i++) {
            int u = sc.nextInt(), v = sc.nextInt();
            g[u].add(v);
            g[v].add(u);

            edges[i][0] = u;
            edges[i][1] = v;
        }

        long inf = Long.MAX_VALUE / 10;
        long[] cost = new long[n + 1];
        Arrays.fill(cost, inf);

        // BFS求最短路
        Deque<Integer> deq = new ArrayDeque<>();
        deq.offer(1);
        cost[0] = cost[1] = 0;
        while (!deq.isEmpty()) {
            int cur = deq.poll();
            for (int v : g[cur]) {
                if (cost[v] > cost[cur] + 1) {
                    cost[v] = cost[cur] + 1;
                    deq.offer(v);
                }
            }
        }

        // 乘法原理阶段
        long mod = 10_0000_0007l;
        long res = 1l;
        int edgeOfShort = 0; // 参与最短路的边
        // 从2开始计算，忽略节点2
        for (int i = 2; i <= n; i++) {
            int cnt = 0;
            for (int v: g[i]) {
                // 保证上流节点
                if (cost[i] == cost[v] + 1) {
                    cnt++;
                }
            }
            edgeOfShort += cnt;

            // 2^z - 1
            long r = ksm(2l, cnt, mod);
            r = ((r - 1) % mod + mod) % mod;

            // 乘法原理
            res = res * r % mod;
        }

        int edgeOfNone = m - edgeOfShort; // 不参与最短路的边数
        res = res * ksm(2l, edgeOfNone, mod) % mod;

        long minCost = Arrays.stream(cost).sum() % mod;
        System.out.println(minCost + " " + res);

    }

}

---

E. 小红打boss

这题挺难贪心的，为啥这么说，因为有多种思路贪心，但是结果并非最优。

但是无论如何贪心

• 两种不同属性依次实施
• 尽量让大的技能伤害double

所以这个贪心，也就变成 最优配对，整体最大化的问题。

来引入一个众数思路

假设 不同属性技能的次数，分别为 a, b, c, 其中c为众数

如果 a + b <= c

分类讨论

• 如果最大数都在集合c中，那一定可以实现a+b=n-c次
• 如果最大数也分布于集合a，b中，那a和b直接选取c的最小元素即可, 等价于交换，也一定能实现a+b=n-c次

如果 a + b > c

由众数定理， 一定可以构建 全是不同属性的pair（若n为奇数，单独留一个尾巴），这样可以实现 n/2个最大数的加倍

---

结合这两个的讨论，可以得出如下的结论

mass = min(n/2, n - max(a, b, c))

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        Map<String, Integer> hash = new HashMap<>();
        hash.put("ice", 0);
        hash.put("fire", 1);
        hash.put("thunder", 2);

        int n = sc.nextInt();
        int[] magic = new int[3];
        int[] attack = new int[n];

        for (int i = 0; i < n; i++) {
            String s = sc.next();
            magic[hash.get(s)]++;
            attack[i] = sc.nextInt();
        }

        Arrays.sort(attack);
        int mass = Math.max(Math.max(magic[0], magic[1]), magic[2]);
        int m = Math.min(n / 2, n - mass);
        long ans = 0;
        for (int i = 0; i < n; i++) {
            if (i >= n - m) {
                ans += attack[i];
            }
            ans += attack[i];
        }
        System.out.println(ans);

    }

}

---

写在最后