三维重建（2）--摄像机标定

发布时间：2024年01月19日

目录

一、最小二乘解

1、线性方程组的解

2、齐次线性方程组的解

3、齐次线性方程组的最小二乘解

4、非线性方程组的最小二乘法

一、最小二乘解

1、线性方程组的解

? ? ? ? 线性方程组Ax=y的解，当矩阵A列满秩情况时，存在三种情况：

（1）行数（方程数）小于未知数个数，欠定方程组，多解。

（2）行数（方程数）等于未知数个数，唯一解。

（3）行数（方程数）大于未知数个数，超定方程组，无解。（除非当y可以由A的列向量线性表示）

2、齐次线性方程组的解

? ? ? ? 对于线性方程组Ax=0的解，当矩阵A列满秩情况时，存在三种情况：

（1）行数（方程数）小于未知数个数，欠定方程组，多解。

（2）行数（方程数）等于未知数个数，只有零解。

（3）行数（方程数）大于未知数个数，超定方程组，除零解外无解。

3、齐次线性方程组的最小二乘解

? ? ? ? 当Ax=0时，对于最小二乘解，也就是求下面这个问题：

????????定义E(x)=\sum_{i=1}^p(a_{i1}x_1+a_{i2}x_2+...+a_{iq}x_q)^2=||Ax||^2，齐次线性方程组最小二乘法的解为x^*=argmin_x||Ax|| \quad s.t.||x||=1。

? ? ? ? 求解方法利用奇异值分解方法。

4、非线性方程组的最小二乘法

? ? ? ? 对于非线性方程为f(x)=0时（区别于线性方程组）当行数大于未知数个数时，最小二乘法的解：

????????定义E(x)=\sum_{i=1}^pf_i^2(x)=||f(x)||^2,非线性方程组最小二乘解为x^*=argmin_x||f(x)||^2。

? ? ? ? 求解方法使用牛顿法和列文伯格-马夸尔特法（L-M法）。

二、摄像机标定问题

1、标定问题

? ? ? ? 首先对于摄像机标定问题，注意像素坐标平面的点用p表示，世界坐标系的点用P表示（不再用P_w表示）。所以有下面变换式成立：?p=MP=K[R\hspace{0.25cm} T]P

? ? ? ? 在标定问题上首先明确一个物体有多个点构成，实物的坐标和像的坐标都是已知的，即世界坐标系的P_1,P_2,P_3位置已知，图像中的p_1,p_2,p_3位置已知，目标是去计算摄像机的内外参数。

? ? ? ? 我们可以定义投影矩阵M为一个三行1×3向量组成的矩阵，即

???????????????????????????????????????????????????????????????????????????????????M=K[R \hspace{0.25cm}T]=\begin{bmatrix} m_1 \\ m_2 \\ m_3 \end{bmatrix}

? ? ? ? 那么像素坐标系的一个点p_i就可以定义为：

????????????????????????????????????????????????p_i=\begin{bmatrix} u_i\\ v_i \end{bmatrix}=\begin{bmatrix} \displaystyle\frac{m_1P_i}{m_3P_i}\\ \displaystyle\frac{m_2P_i}{m_3P_i} \end{bmatrix}

? ? ? ? 此时摄像机投影矩阵有11个自由度（未知量），但是应该有12个未知量，第12个未知量是由前11个未知量线性变换而来。由于每一个点在像素坐标系下为二维的两个值，那么对于11个未知量来说最少需要12个方程来进行求解（由于像素坐标系下点的两个横纵坐标成对出现），那么就需要六对点来对应，但实际应用中一定是使用多于六对点来对应，通过最小二乘法消掉一部分错误的噪声点对，获得更好的鲁棒性效果。

? ? ? ? 下面公式就是将任意一个像素坐标系上的点，通过等式变换得到一个齐次线性方程，而多个点对又构成了齐次线性方程组。

? ? ? ? 大多数情况下，生成的齐次线性方程数是远大于11的，方程数大于未知参数，齐次线性方程组为一个超定方程组，所以可以用齐次线性方程组的最小二乘法求解方法来求解同样的问题。

2、提取摄像机参数

????????

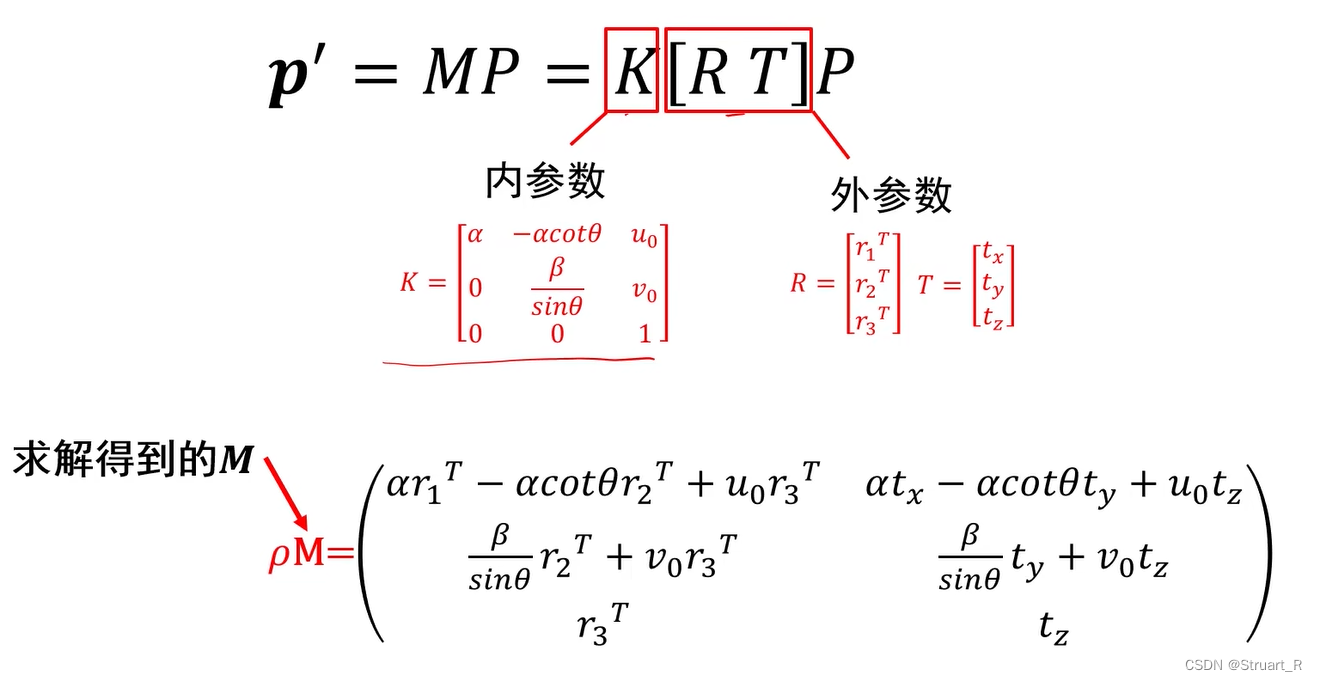
文章来源:https://blog.csdn.net/m0_60177079/article/details/135686744
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章