二叉树及其实现
发布时间:2024年01月10日
二叉树
一.树的概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
1.2相关概念
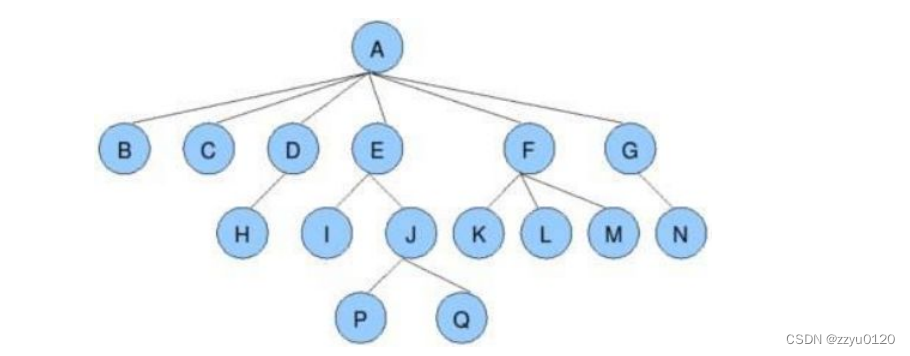
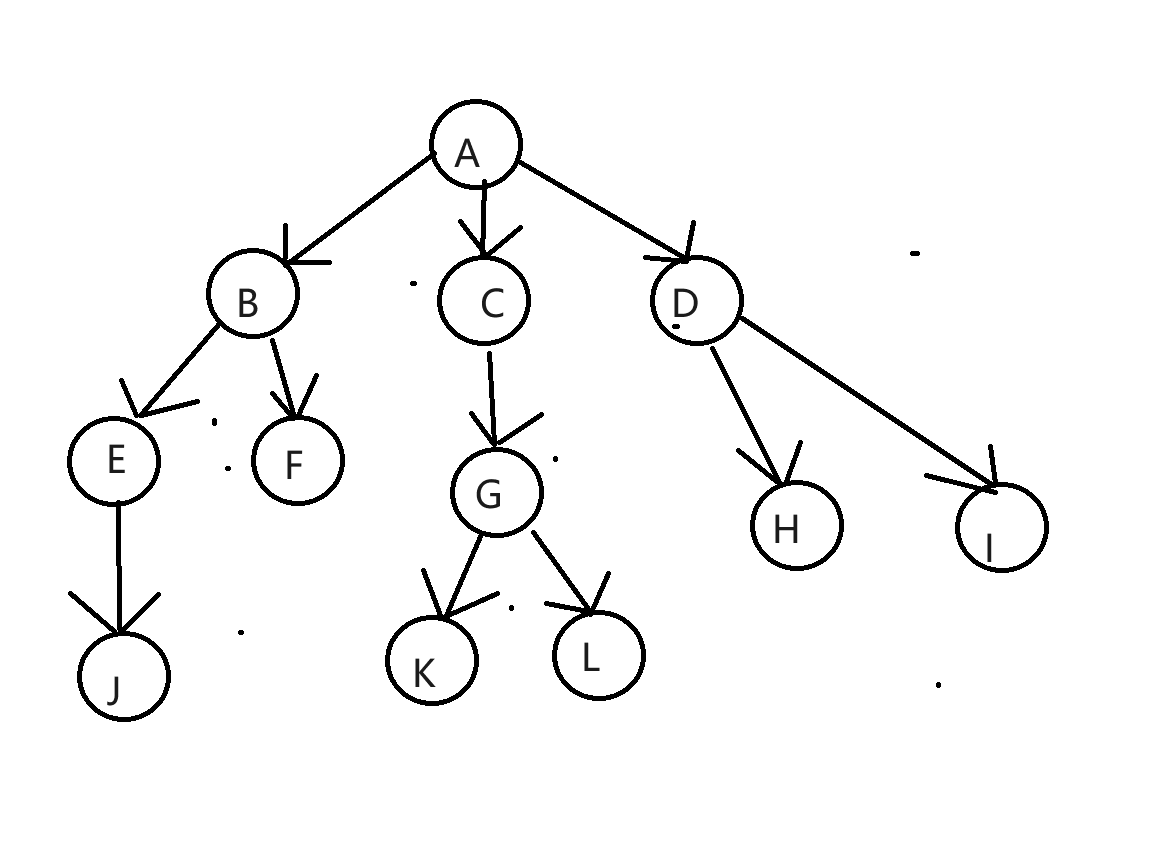
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点;具有相同父节点的节点互称为兄弟节点 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
2.二叉树的概念及结构
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
- 为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
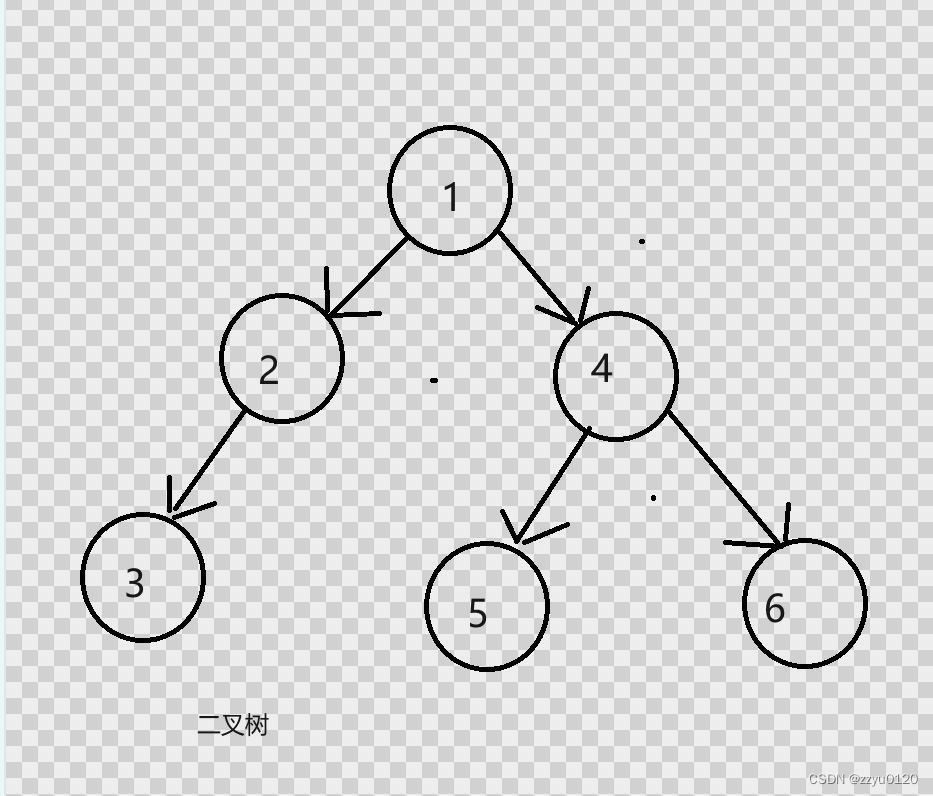
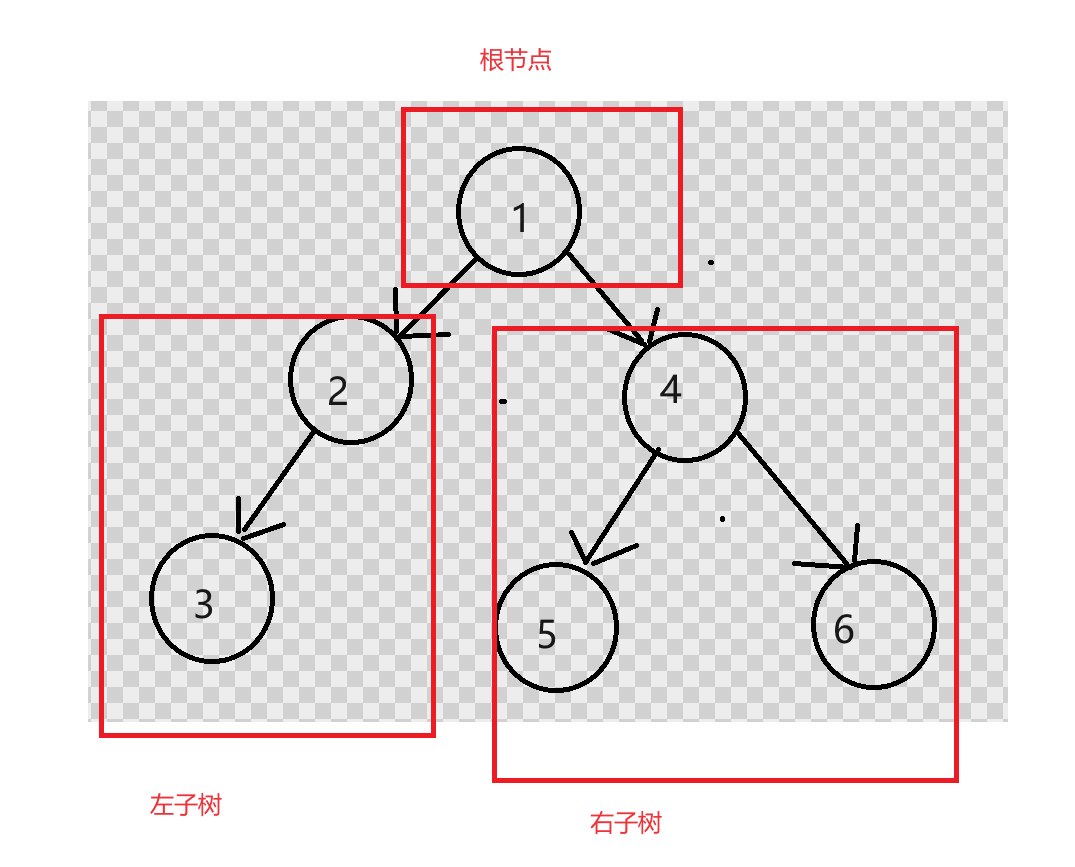
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2.2 特殊的二叉树
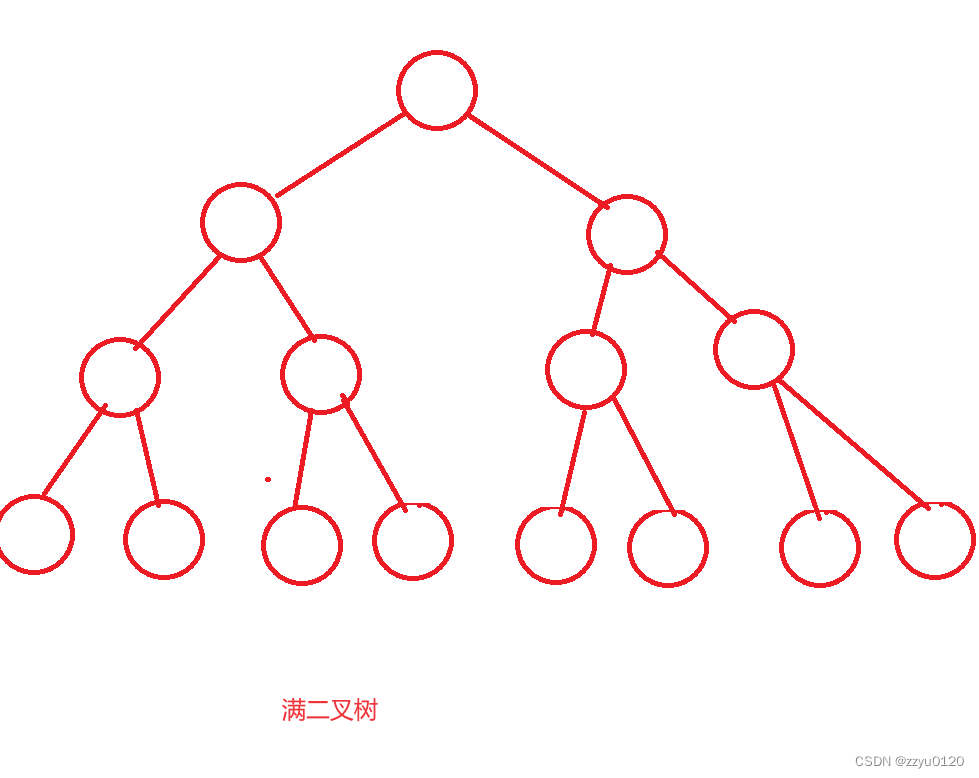
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。
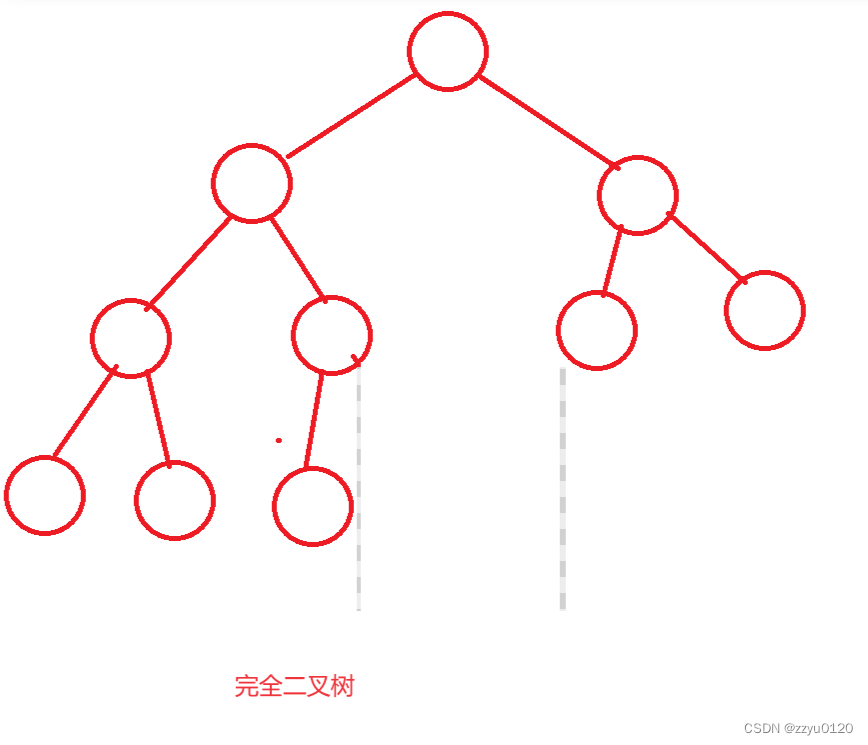
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
3.二叉树的遍历
3.1 前序、中序以及后序遍历
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
void PrevOrder(BTNode* root) {//前序
if (root == NULL) {
printf("NULL ");
return;
}
printf("%d ", root->val);
PrevOrder(root->left);
PrevOrder(root->right);
}
void InOrder(BTNode* root)//中序
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
void PostOrder(BTNode* root)//后序
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
3.2 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
void LevelOrder(BTNode* root)
{
Que q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->val);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
QueuePop(&q);
}
printf("\n");
QueueDestroy(&q);
}
3.3 判断二叉树是否是完全二叉树
int TreeComplete(BTNode* root)
{
Que q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
QueuePop(&q);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
3.4 二叉树的高度
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}
3.5 二叉树的叶子节点个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
3.6 二叉树的第k层的节点个数
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
{
return 1;
}
return TreeKLevel(root->left, k - 1)
+ TreeKLevel(root->right, k - 1);
}
3.7 二叉树销毁
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
//root = NULL;
}
3.7 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* ret = NULL;
ret = TreeFind(root->left, x);
if (ret)
return ret;
ret = TreeFind(root->right, x);
if (ret)
return ret;
return NULL;
}
文章来源:https://blog.csdn.net/qq_63168095/article/details/135514028
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Android studio 花式按键
- 文心一言 VS 讯飞星火 VS chatgpt (165)-- 算法导论13.1 5题
- Python 使用 python-dateutil 获取间隔时间
- GPT-4 API曝重大安全漏洞,研究人员成功越狱; Pika 1.0 全面开放免费试用!
- 入门Python笔记详细介绍
- C# 请求服务端方式1
- [足式机器人]Part4 南科大高等机器人控制课 Ch08 Rigid Body Dynamics
- Python 创建第一个项目
- Linux进阶命令合集
- HarmonyOS:Neural Network Runtime 对接 AI 推理框架开发指导