面向对象之深度优先和广度优先

面向对象深度优先和广度优先是什么？

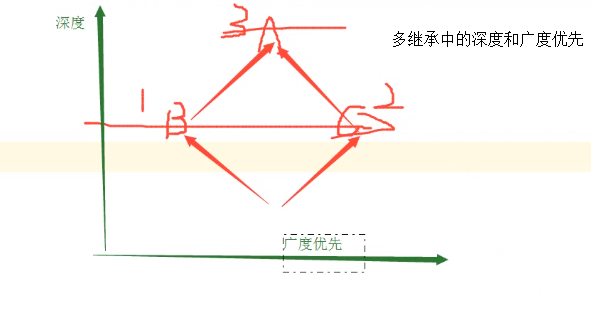
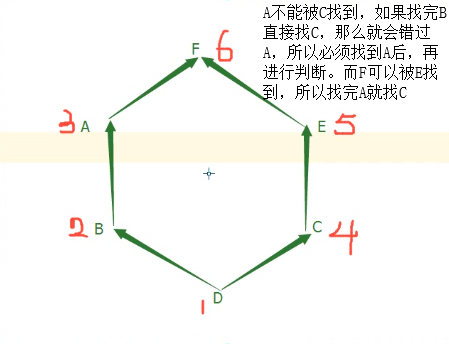
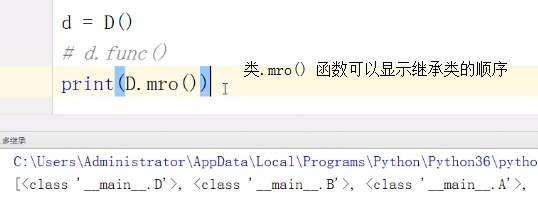
二叉树的两种遍历是数据结构的经典考察题目, 广度遍历考察队列结构, 深度遍历考察递归

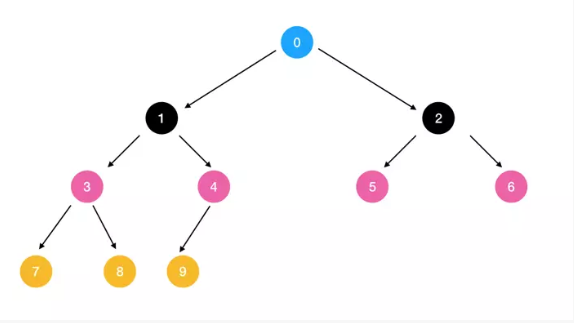
深度优先

先序遍历(父,?左子,?右子)?0,?1,?3,?7,?8,?4,?9,?2,?5,?6
中序遍历(左子,?父,?右子)?7,?3,?8,?1,?9,?4,?0,?5,?2,?6
后序遍历(左子,?右子,?父)?7,?8,?3,?9,?4,?1,?5,?6,?2,?0

"深度优先遍历"考察递归, 将子节点为空作为终止递归的条件

广度优先

"广度优先遍历"考察队列的结构,?消除父节点(出队列,顺便打印),?添加子节点(进队列),当队列内元素个数为零,?完成遍历

添加元素

广度优先遍历

深度优先

Python3 实现

class?Node(object):
????"""初始化一个节点,需要为节点设置值"""
????def?__init__(self,?val):
????????self.val?=?val
????????self.left?=?None
????????self.right?=?None
class?BinaryTree(object):
????"""
????创建二叉树,完成
????-?添加元素
????-?广度遍历
????-?深度遍历(先序遍历,?中序遍历,?后序遍历)
????"""
????def?__init__(self):
????????self.root?=?None
????????pass
????#?添加元素
????def?addNode(self,?val):
????????#?创建队列结构存储结点
????????nodeStack?=?[self.root,]
????????#?如果根结点为空
????????if?self.root?==?None:
????????????self.root?=?Node(val)
????????????print("添加根节点{0}成功!".format(self.root.val))
????????????return
????????while?len(nodeStack)?>?0:
????????????#?队列元素出列
????????????p_node?=?nodeStack.pop()
????????????#?如果左子结点为空
????????????if?p_node.left?==?None:
????????????????p_node.left?=?Node(val)
????????????????print("添加左:{0}?".format(p_node.left.val))
????????????????return
????????????#?如果右子节点为空
????????????if?p_node.right?==?None:
????????????????p_node.right?=?Node(val)
????????????????print("添加右:{0}?".format(p_node.right.val))
????????????????return
????????????nodeStack.insert(0,?p_node.left)
????????????nodeStack.insert(0,?p_node.right)
????#?广度遍历(中序:?先读父节点,再读左子节点,?右子节点)
????def?breadthFirst(self):
????????nodeStack?=?[self.root,?];
????????while?len(nodeStack)?>?0:
????????????my_node?=?nodeStack.pop()
????????????print("-->",my_node.val)
????????????if?my_node.left?is?not?None:
????????????????nodeStack.insert(0,?my_node.left)
????????????if?my_node.right?is?not?None:
????????????????nodeStack.insert(0,?my_node.right)
????#?深度优先(先序遍历)
????def?preorder(self,?start_node):
????????if?start_node?==?None:
????????????return
????????print(start_node.val)
????????self.preorder(start_node.left)
????????self.preorder(start_node.right)
????#?深度优先(中序遍历)
????def?inorder(self,?start_node):
????????if?start_node?==?None:
????????????return
????????self.inorder(start_node.left)
????????print(start_node.val)
????????self.inorder(start_node.right)
????#?深度优先(后序遍历)
????def?outorder(self,?start_node):
????????if?start_node?==?None:
????????????return
????????self.outorder(start_node.left)
????????self.outorder(start_node.right)
????????print(start_node.val)
def?main():
????bt?=?BinaryTree()
????bt.addNode(0)
????bt.addNode(1)
????bt.addNode(2)
????bt.addNode(3)
????bt.addNode(4)
????bt.addNode(5)
????bt.addNode(6)
????bt.addNode(7)
????bt.addNode(8)
????bt.addNode(9)
????print("广度遍历-->")
????bt.breadthFirst()
????
????print("先序遍历-->")
????bt.preorder(bt.root)
????print("中序遍历-->")
????bt.inorder(bt.root)
????
????print("后序遍历-->")
????bt.outorder(bt.root)
if?__name__?==?'__main__':
????main()