从入门到精通,30天带你学会C++【第十一天:二分查找】
发布时间:2024年01月01日
目录
Everyday English
Look before you leap.
三思而后行
前言
今天是2024年的第一天,新一年,新气象,新起点,在这也祝愿大家:
工作顺利,身体健康。好好学习,天天向上!
二分查找
二分法我们在上节课已经介绍过了,这节课我们来实现二分查找。
没看过的一定要先看:
例题
先看题目:给定一个长度为n序列和一个整数m,问:这个序列里面有没有m?
50分做法
分析利弊
把整个数组遍历一遍,看看有没有m。
优点:简单粗暴,容易想到。
缺点:数据一多,轻松超时。
示例代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,m,a[100000];
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
if(a[i]==m)
{
cout<<"Yes"<<endl;
return 0;
}
}
cout<<"No"<<endl;
return 0;
}示例截图

100分做法
这就需要用到我们的二分查找了。
注意:二分查找一定要是有序的序列!
二分查找是什么?
回忆一下我们上次的猜数游戏的必胜策略,从始至终都是有一个范围的,我们通过不断地把范围二分缩小,最终得到答案。
在二分查找中也要有一个范围,或者叫区间。在这个区间有两个端点,分别叫左端点和右端点。
那我们二分还得有个中点,就像猜数游戏每次都要猜区间地一半一样。
而中点地计算方法是:(左端点+右端点)/ 2
为了方便描述,我们在编程中一般把左端点叫作left,右端点叫作right,中点叫作mid。
这题该怎么用二分查找?
我们可以先把序列用sort排序一下,紧接着确定好左右端点及mid。
其实这两个端点就像两个指针一样
如果left+1==right的话,说明两个指针不能在缩小了,此时,如果还未找到输出no。
示例代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,m,a[100000],left,right,mid;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
left=1; right=n;
while(left+1!=right)
{
mid=(left+right)/2;
if(a[mid]>m) right=mid-1;
if(a[mid]<m) left=mid+1;
if(a[mid]==m)
{
cout<<"Yes"<<endl;
return 0;
}
}
cout<<"No"<<endl;
return 0;
}示例截图
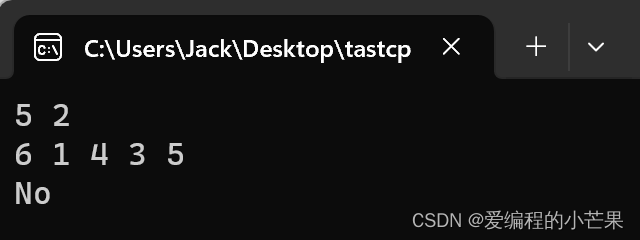
结尾
最后认识一下,我是爱编程的小芒果,一个爱编程的小学生,我们2024年见!
文章来源:https://blog.csdn.net/m0_73787047/article/details/135323974
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 5G应用逐浪数字化之巅, 开创高质量发展新局面!
- Android开发实用Navigation怎么改变导航栏图标、字体颜色,如何去掉标题栏?请看这里。
- AWS CI/CD之二:配置CodeDeploy
- 如何查看Ubuntu内存的使用情况
- 刷题第五十一天 84. 柱状图中最大矩形
- Zabbix公告多个安全漏洞,涉及多个版本(附修复方案)
- 内网环境横向移动——利用DCOM(1)
- RHCE8 资料整理(十一)
- 读元宇宙改变一切笔记01_起源
- 面对AI革新时,Soul App等社交应用的“出圈”解法是什么?