LLM预备知识——概念、技术基础篇

transformer模型结构

1、基础神经网络

1、CNN：卷积神经网络

• 包括Cov卷积层、pool池化层，方便并行计算；详细介绍略过。
• Cov卷积层：可以定义num_filter个卷积核进行卷积操作，然后将各结果concat；
• pool池化层：也可以称为下采样，一般包括两种方式：最大值下采样max_pooling、平均值下采样mean_pooling。

2、RNN：循环神经网络

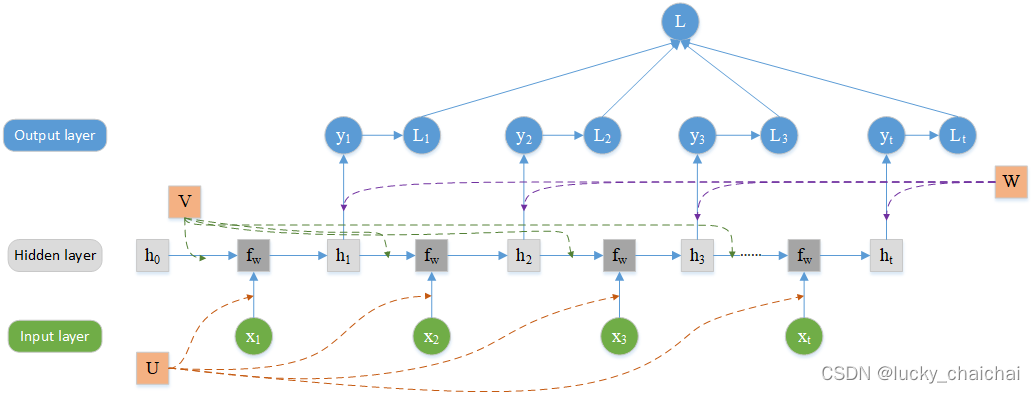
（1）正向单个计算过程网络结构：

• x₁, x₂,…为一个序列化的输入序列，比如一段文本；
• 每层参数共享，图中U为输入层和隐藏层之间的权重，V为隐藏层之间的权重，W为隐藏层与输出层之间的权重；
• RNN可以有一个输出，也可以有多个输出（例如“序列标注”问题），下图是多个输出的过程，若仅一个输出，则只有一个y_t；
• L为最终的loss；
• 缺点是，无法并行执行。
  
  （2）与上图对应的公式
• 隐藏层的计算：h_t = f_w(h_t-1, x_t) = tanh(V × h_t-1 + U × x_t)
• 输出层的计算：y_t = softmax(W × h_t)

3、LSTM：长短期记忆神经网络

• 传统RNN的变种（以下述RNN为例，在h₀后添加忘记门，x₁上添加输入门，h₁之前添加输出门），可解决序列化数据的长期依赖问题；
• LSTM的模型结构图，其中亮蓝色为忘记门，红色为输入门，黑色为更新当前细胞状态 C_t 操作，绿色为输出门。
  
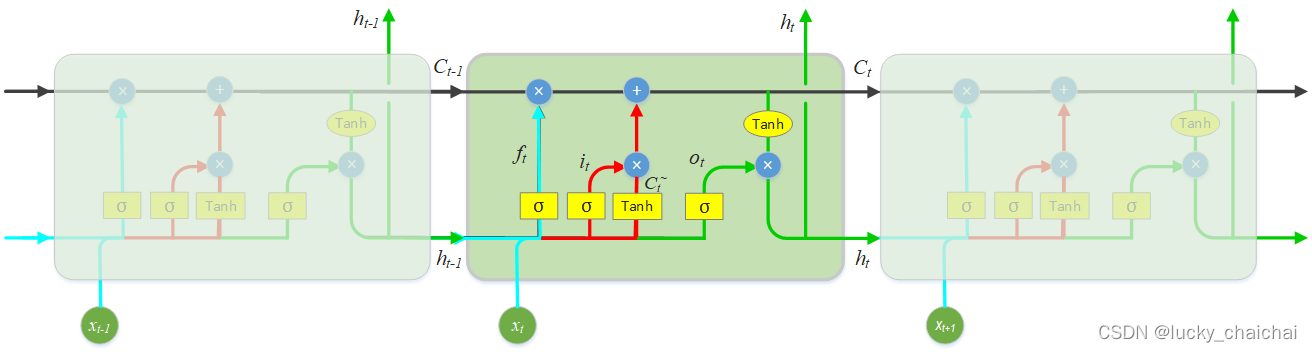
  • LSTM的输入有三个：C_t-1、h_t-1和x_t，输出有两个：C_t、h_t；
  • f_t 、 i_t、o_t的计算方式基本相同，只不过使用的参数不共享，计算过程中 [h_t-1, x_t]的结合过程是直接横向concat，比如h_t-1是128维的向量，x_t为28维的向量，concat后为156维向量。
  • 对于忘记门：
    控制当前细胞需要忘记的上一个细胞状态信息比例。该比例通过h_t-1、x_t作为输入来计算得到， σ一般为sigmoid函数，具体计算公式：
    f_t = σ(W_f · [h_t-1, x_t] + b_f)
  • 对于输入门：
    控制当前细胞需要存什么信息，以及保存这些信息的比例。 tanh操作h_t-1、x_t两个输入来计算需要存的当前细胞状态信息候选值C_t^~ ，σ操作h_t-1、x_t来决定保存的信息比例，具体公式如下：
    i_t = σ(W_i · [h_t-1, x_t] + b_i)
    C_t^~ = tanh(W_c · [h_t-1, x_t] + b_c)
  • 更新当前细胞状态：
    更新当前细胞状态，即计算当前细胞状态需要保留上一细胞状态多少信息，加上当前细胞状态信息候选值的保留比例，具体公式如下：*为矩阵对应元素相乘，非矩阵乘法（点乘）
    C_t = f_t * C_t-1 + i_t * C_t^~
  • 对于输出门：
    决定当前细胞输出的内容，以及输出内容的比例。输出内容由tanh操作C_t来计算得到，输出比例由σ操作h_t-1、x_t计算得到，具体公式如下：
    o_t = σ(W_o · [h_t-1, x_t] + b_o)
    h_t = o_t * tanh(C_t)

2、transformer

内容参考自论文《Attention is all you need》

1、attention机制

（1）attention计算过程
在实际计算过程中Q、K、V是作为矩阵同时计算的，所以，整体计算公式表达如原论文中所示：

• 其中Q∈R^n×d_k, K∈R^m×d_k, V∈R^m×d_v分别是输入的序列X = (x₁, …, x_i, …, x_n)，x_i∈R^d_x经过W^Q、 W^K 、W^V得到的矩阵；
  

• 原文中提到：QK^T点乘后除以√d_k的目的是，当d_k很大时，防止点乘之后结果过大，再经过softmax函数时出现梯度消失问题。

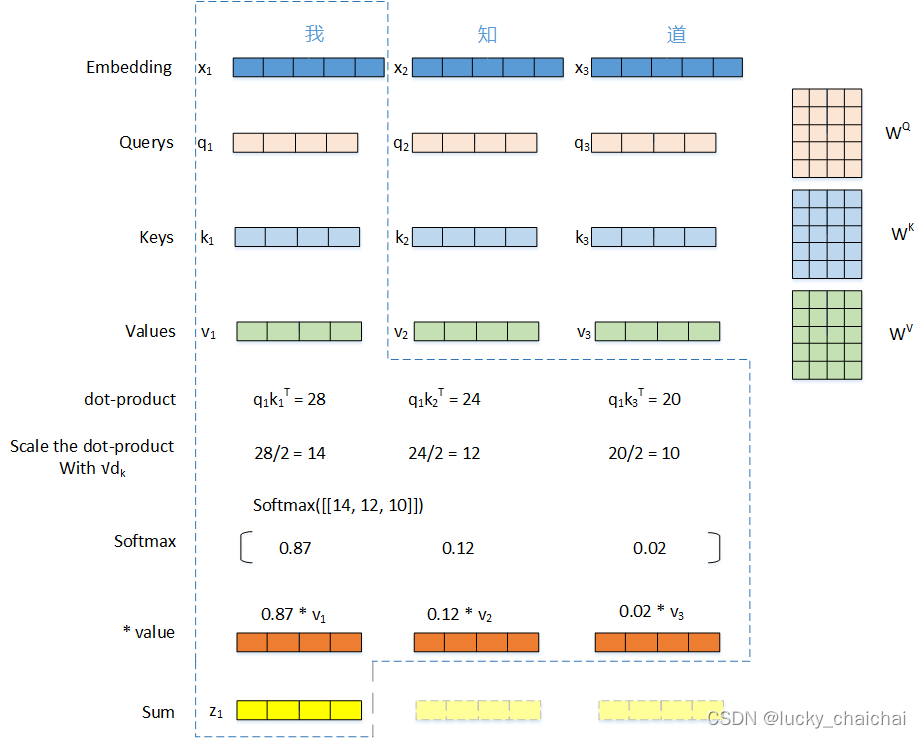
若将上式展开，逐个向量计算，则针对文本序列，以第一个词（字）为例，该词在整个序列中的attention计算过程如下如：

• 计算公式理解如下：
  
  
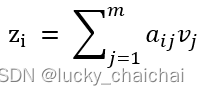
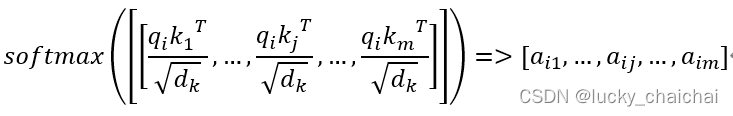
• 公式计算过程图形化后如下所示：
  • 处理的文本序列为“我知道”；
  • 其中，d_x=5，d_v=d_k=4，
    

（2）multi-head attention

• 流程：
  ① 定义h个头；
  ② 将Q、K、V分别使用各个头的参数矩阵（W_i^Q、W_i^K、W_i^V）线性映射一下，i∈[1, h]，映射h组；
  ③ 得到h组Q、K、V，分别进行attention操作，得到h个头的注意力计算结果head；
  ④ 最终将h个head进行concat，然后经过与参数矩阵W^O的计算，得到多头注意力的最终结果。
• 公式表达如下：
  ? Multi-Head(Q,K,V) = concat(head₁, head₁,…, head_h)W^O
  ?其中，head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)

（3）self-attention

• self-attention在序列内部进行attention计算，关注序列内部之间的联系。
• 具体计算方式是Q=K=V=X，也就是计算Attention(X, X, X)

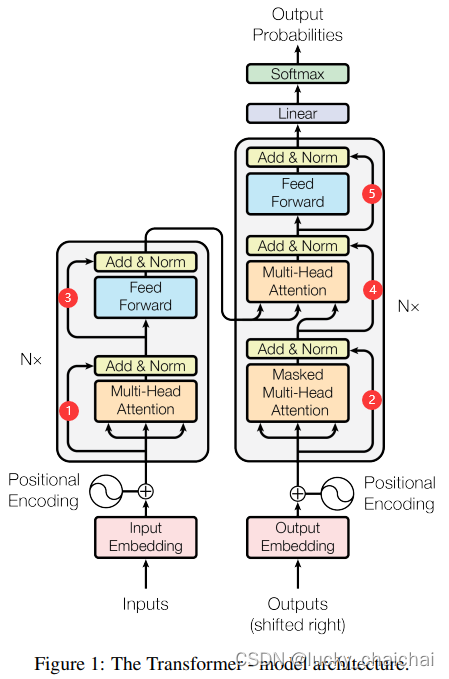
2、传统transformer结构详细解析

• 位置编码：在最初的结构中（如下图），位置编码是在输出上使用表示绝对位置信息的“正余弦位置编码”，后续版本优化了attention结构，在其中加入“相对位置编码”（关于位置编码详见词向量训练实战——Word2vector、Glove、Doc2vector、position_embedding）；
• 位置编码 pos_embd 的维度与输入的编码 inpt_embd 维度相同（与attention部分讲解对应，即为d_x），inpt_embd + pos_embd作为encoder、decoder的输入；
• 有6个encoder、6个decoder；
• encoder结构：多头注意力计算、残差连接、归一化层、全连接前馈网络、残差连接、归一化层。
  • Add & Norm：
    （1）即残差连接 和 归一化，下面提到的Sublayer在encoder中为多头注意力计算和全连接前馈网络；
    （2）也就是下图中①、②、③、④、⑤所标注的模块；
    （3）计算方式：LayerNorm(x + Sublayer(x)) ；
    （4）其实就是，下层的输入 x 与下层的输出 Sublayer(x) 进行向量加法Add操作，然后归一化LayerNorm。（在原作中，为了方便这种残差连接操作，所有sub-layers的输出，包括embedding的结果，向量维度都为d_model=512）；
    （5）LayerNorm的操作：a_2 * (X - mean) / (std + eps) + b_2，其中a_2、b_2为参数矩阵，X为输入矩阵，mean为X的期望，std为X的标准差，eps=1e-6。
  • 多头注意力计算：
    计算过程中，为了使得该层的最终输出维度是d_model，每个头的d_v=d_k=d_model/h.
  • 全连接前馈网络 ：
    （1）公式：FFN(x) = max(0, xW₁ + b₁)W₂ + b₂
    （2）Another way of describing this is as two convolutions with kernel size 1。
• decoder结构：加入mask机制的多头注意力计算、残差连接、归一化层、针对encoder结果的多头注意力计算、残差连接、归一化层、全连接前馈网络、残差连接、归一化层。
  • decoder中对outputs的mask目的：位置 i 处的预测仅依赖于已知的 i 位置之前的输出，mask的目的是防止位置关注后续位置。
    

CRF：条件随机场模型

1、定义

（1）条件随机场（CRF）
设X、Y为随机变量，P(Y|X)是在给定X的条件下Y的条件概率分布。若随机变量Y构成一个由*无向图G=(V,E)*表示的马尔科夫随机场，即
P(Y_v|X,Y_w,w≠v) = P(Y_v|X,Y_w,w~v)
对任意定点v成立，则称条件概率分布P(Y|X)为条件随机场。
其中：
w~v表示在图G=(V,E)中与顶点v有边连接的所有定点w；
w≠v表示除定点v以外的所有顶点；
Y_v与Y_w为顶点v与w对应的随机变量。

• 马尔科夫随机场：具有马尔科夫性的随机场；
  • 随机场：设T是一无限实数集，把依赖于参数t∈T的一簇（无限多个）随机变量称为随机过程；若T为n维空间的某个子集，t则为一个n维向量，此时随机变量又称为随机场；
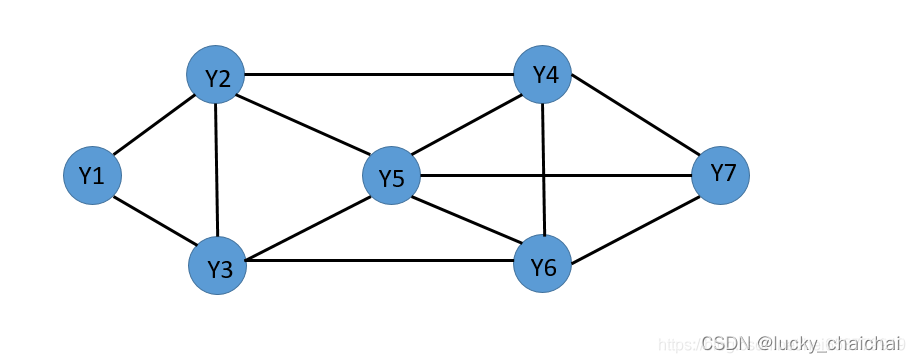
  • 马尔科夫性：P(Y_v|X,Y_w,w≠v) = P(Y_v|X,Y_w,w~v)
  • 例如：对于顶点Y₁，P(Y₁|X,Y_w) = P(Y₁∣X,Y₂,Y₃)
    

（2）线性CRF
设X =(X₁,X₂,…,X_n)，Y = (Y₁,Y₂,…,Y_n)均为线性表示的随机变量序列，若在给定随机变量序列X的条件下，随机变量序列Y的条件概率分布P(YIX)构成条件随机场，即满足马尔可夫性
P(Y_ilX,Y₁,…,Y_i-1,Y_i+1,…,Y_n) = P(Y|X,Y_i-1,Y_i+1)
则称P(YIX)为线性链条件随机场。
其中i = 1,2,…,n，在i = 1和n 时只考虑单边。

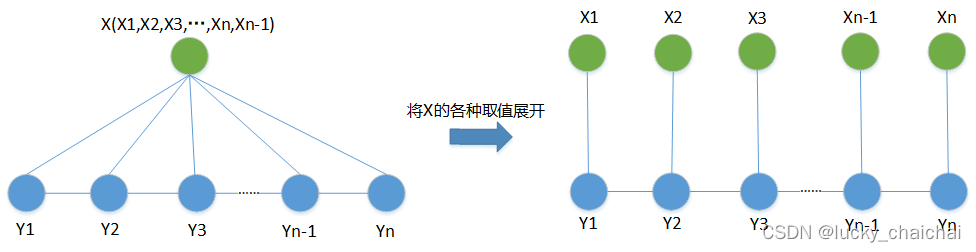
• 一般（比如NER任务中）随机变量序列X又称为观察序列，Y为状态序列;
• X、Y之间可以表示为下图，也就是说，在给定X的情况下，当前状态Y_i仅跟与其相连接的状态Y_i?1相关。
  

2、基于CRF的实践代码（NER）

详见：知识图谱中“三元组”抽取——Python中模型总结实战（基于TensorFlow2.5）5.1小节基于BiLSTM+CRF实现NER