红黑树学习记录

数组

1. 连续的内存空间
2. 相同类型的数据

线性查找的时间复杂度：

• 最好情况：第一个元素即匹配成功，时间复杂度为O(1)；
• 最坏情况：最后一个元素才匹配成功或者元素不存在，时间复杂度为O(n)。

二分查找的时间复杂度：

• 前提是有序数组；
• 取数组的中间元素与目标元素进行比较，如果相等则返回，否则根据比较结果缩小查找范围，继续查找，时间复杂度为O(logn)。

二分查找树

对任一节点而言，其左子树的所有节点都小于该节点，其右子树的所有节点都大于该节点

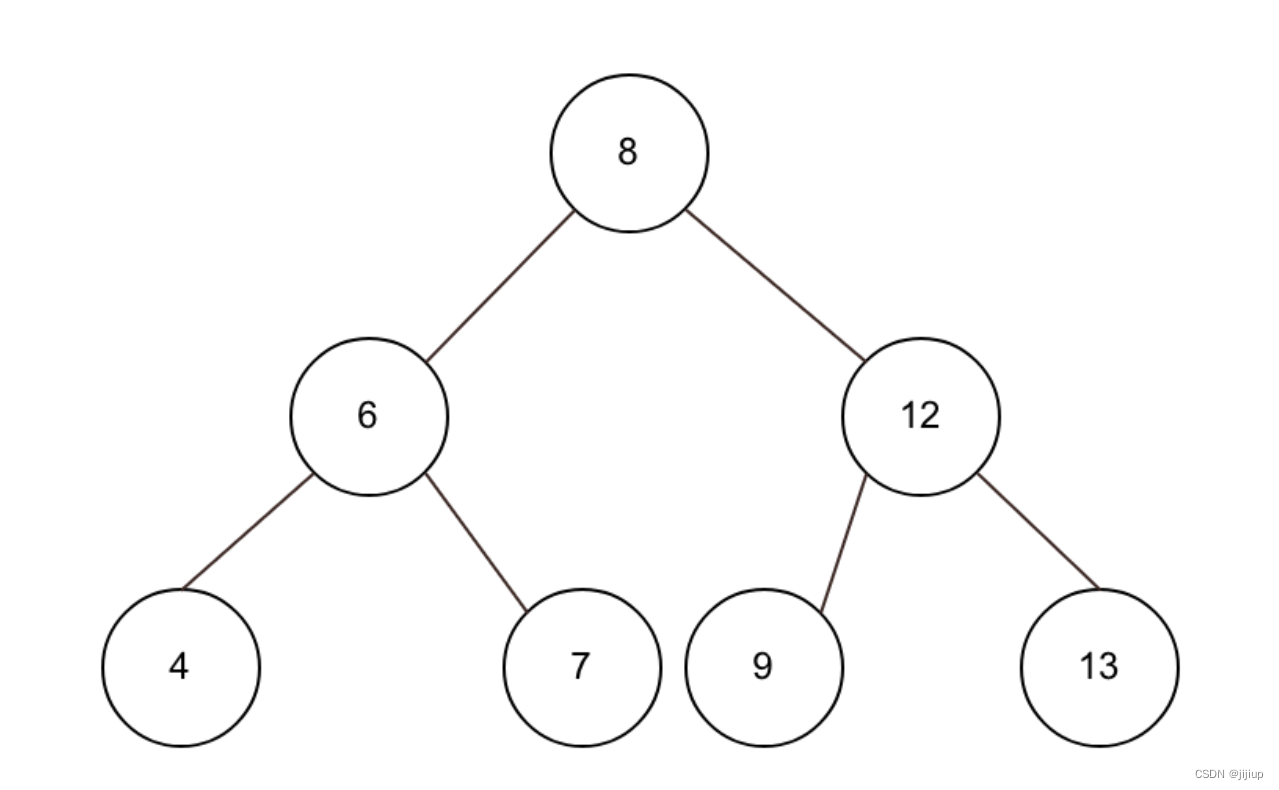
查找值为7的节点：

1. 7小于根节点8，则进入左子树进一步查找；
2. 7大于节点6，则进入右子树进一步查找；
3. 7等于节点7，找到。

时间复杂度O(logn)

但是

如果存在极端情况，每次节点插入时都是最大或最小的元素，那么二叉查找树就退变成一条链表啦😱

这样查找的时间复杂度最坏情况下就变成了O(n)

不行要做出改变！

平衡二叉查找树 AVL树

1. 同样具有二叉查找树的特性
2. “平衡”，对任一节点而言，左右子树的高度差不超过1

增加或删除元素时，通过左旋、右旋操作维持平衡

首先找到其左右子树失衡的节点，例如下图中节点9的左右子树失衡了，高度差超过1

左旋：失衡节点指向其右孩子的左孩子

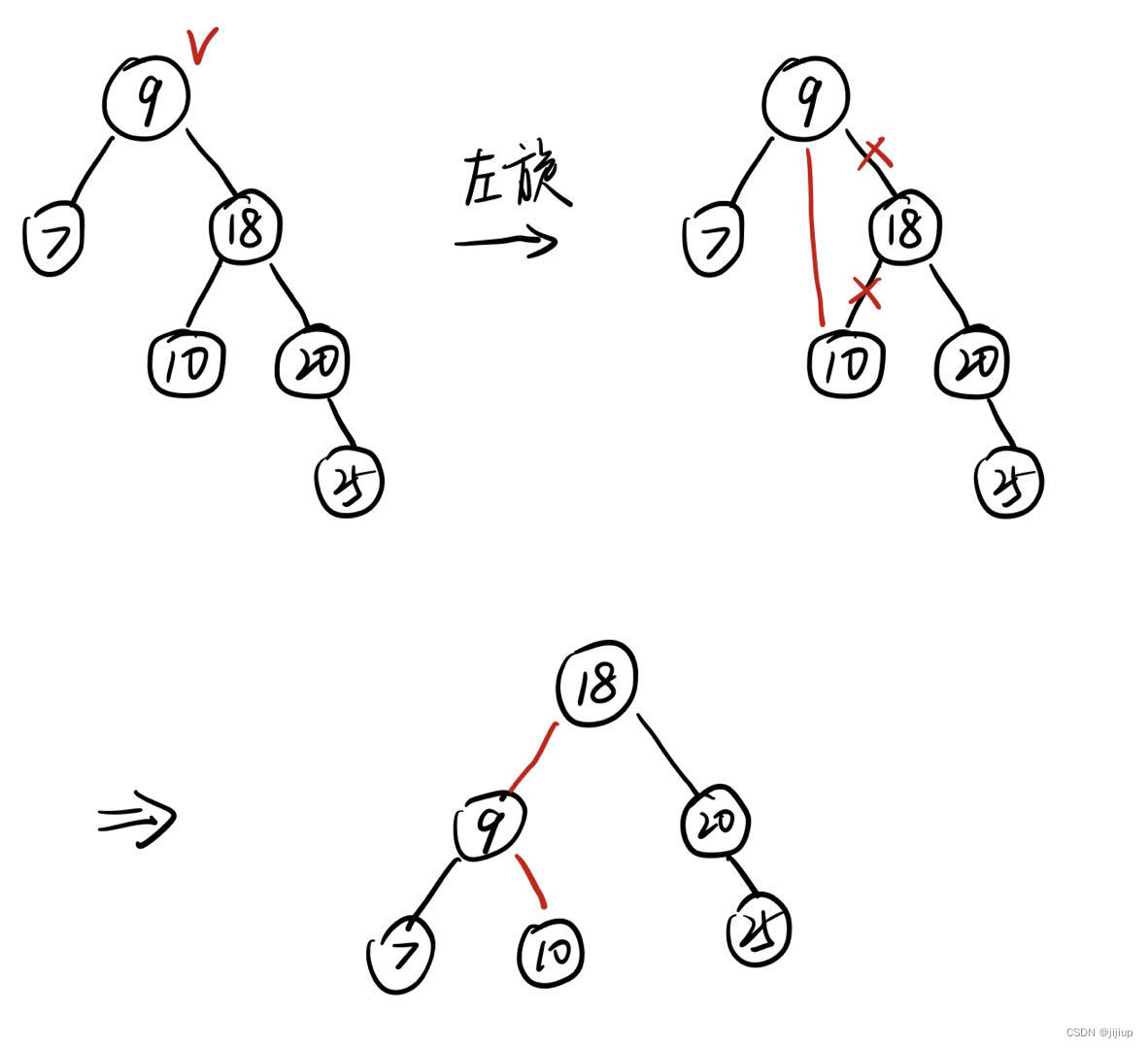
右旋：失衡节点指向其左孩子的右孩子

红黑树

1. 节点不是黑色就是红色

2. 根节点一定是黑色

3. 叶子节点（NIL）一定是黑色

4. 每个红色节点的两个子节点都为黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）

5. 从任一节点到其每个叶子节点NIL的所有路径，都包含相同数目的黑色节点（黑高）

查找、插入、删除的时间复杂度为O(logn)

一般在插入红黑树节点的时候，会将这个节点设置为红色，?红色破坏原则的可能性最小，如果是黑色, 很可能导致这条支路的黑色节点比其它支路的要多1，破坏了平衡。

AVL树的平衡比较严格，在进行频繁的插入删除操作时，为了保持左右子树的高度差不超过1的平衡条件，需要进行频繁的旋转操作来维持平衡。与AVL树相比，红黑树牺牲了部分平衡性，以换取插入/删除操作时较少的旋转操作，整体来说性能要优于AVL树。

参考资料

红黑树（图解+秒懂+史上最全） - 疯狂创客圈 - 博客园 (cnblogs.com)