力扣精选算法100题——在排序数组中查找元素的第一个和最后一个位置(二分查找专题)

目录

第一步：了解题意?

第二步：算法原理

🚩查找区间左端点值

?处理细节

循环条件：

求中点

🚩查找区间右端点值

?处理细节

循环条件

求中点

🚩总结

第三步：代码实现

第四步:总结模板

---

第一步：了解题意?

• 本题是返回的是（在数组中与目标值相等的开始位置和结束位置)如果是{1,2,3,3,3,4,5}我们只需返回{2，4}位置即可，只要返回开始位置和结束位置，中间位置不用返回
• 如果不存在目标值target，那么我们就返回{-1,-1}?

---

第二步：算法原理

这一题暴力解法确实是很简单的去实现，但是这一题明确说明了需要时间复杂度为logN来实现，这就意味着不能用暴力解法O(N)。

二分查找法的本质：看区间是否有“二段性”。取一个点能分成俩部分，有一部分是满足条件，则可用二分查找算法。它并不是非得分成一半一半，也可以是三分之一，四分之一，只是复杂度的问题。

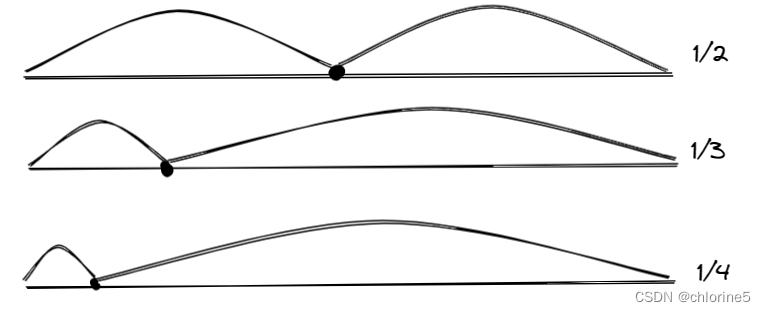
其实我们可以利用三分四分二分都可以解决问题，但是我们最合理的是二分方法解决问题，因为用到概率学的期望值中，我们确实如果找到目标值可以在1/4中的小部分，但是我们也可能在1/4的另一个大部分，所以期望值来看，平分是最好的。最终选取中间点进行划分，二分查找时间复杂度最小。

---

本题是找到开始位置和结束位置，我们可以从查找区间的左端点值和区间的右端点值入手。

🚩查找区间左端点值

我们看到这里，我们会不会想到划分区间（二分查找的本质是'能有“二分段”）我们可以划分【小于t】【大于等于t】俩部分。这时候我们就可以二分查找思路来解题。

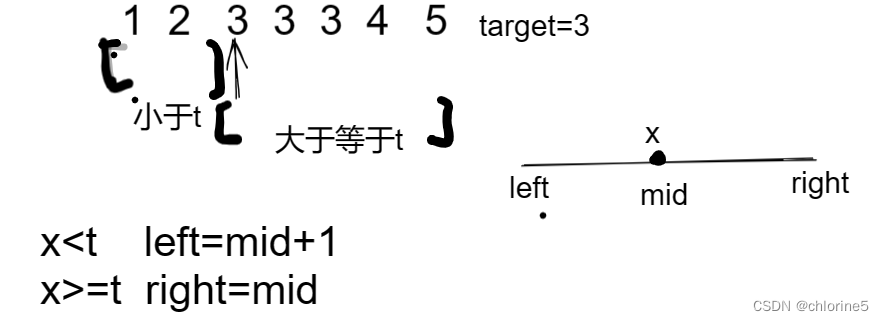
• 由于x<t的话肯定在小于t的区间内，那里面的结果是不可能存在等于target的所以我们给left=mid+1
• 而x>=t的时候，肯定是在大于等于t的区间内，所以里面的结果是可能存在等于target的，如果mid正好对应的是等于最左边的3的时候，我们是不能给right=mid-1的，所以我就给right=mid即可

---

?处理细节

循环条件：

存在俩种情况left<=right和left<right。

最终left是肯定会达到区间的左端点的值的，而right=mid一直在靠近最左端值，最终也会到达端点值，所以我们不需要进行left=right再循环，因为那个时候我们已经指向了结果，我们只需要判断一下left对应的值是否等于target即可。

最终选择left<right.

求中点

求中点：

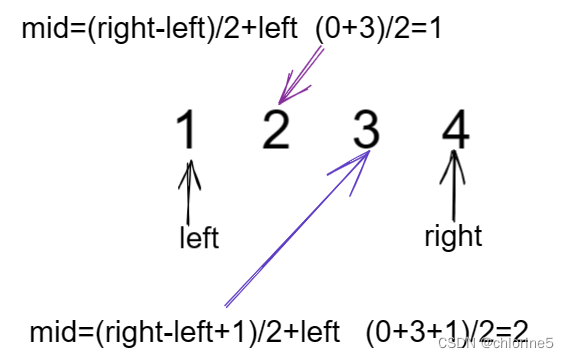
mid=left+(right-left)/2

mid=left+(right-left+1)/2

这俩个中点值，一个值的是在偶数的时候取左值还是右值。

而我们在取区间的左端的时候，我们的left=mid+1??right=mid.

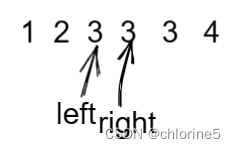如果我们选择mid=(right+left+1)/2+left的情况下，我们在遇到这个情况下，mid在right的位置，然后right依旧mid，我们就陷入了死循环，我们需要mid指向的是偶区间的左边，而不是右边，因为right=mid，会导致死循环。所以遇到查找区间的左端点值我们选择mid=(right-left)/2+left

🚩查找区间右端点值

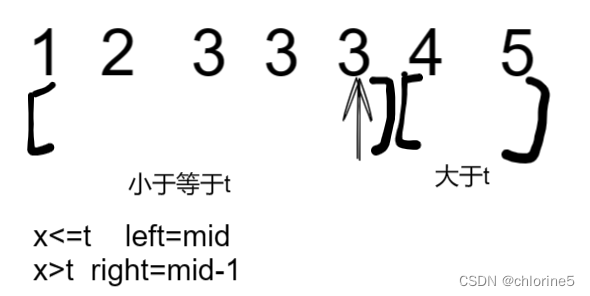
• 由于x>t的话肯定在大于t的区间内，那里面的结果是不可能存在等于target的所以我们给right=mid-1
• 而x<=t的时候，肯定是在小于等于t的区间内，所以里面的结果是可能存在等于target的，如果mid正好对应的是等于最左边的3的时候，我们是不能给left=mid+1的，所以我就给left=mid即可

?处理细节

循环条件

和上述的查找区间的左端点值一样。

求中点

而我们在取区间的右端点的时候，我们的left=mid? right=mid-1.

如果我们选择mid=(right+left)/2+left的情况下，我们在遇到这个情况下，mid在left的位置，然后left依旧mid，我们就陷入了死循环，我们需要mid指向的是偶区间的右边，而不是左边，因为left=mid，会导致死循环。所以遇到查找区间的右端点值我们选择mid=(right-left+1)/2+left

---

🚩总结

• 循环条件：left<right

区间左端点，区间右端点我们都不需要再进行left=right的循环，所以循环条件是left<right

• 求中点：

区间左端点：mid=(right-left)/2+left? ? 因为left=mid+1? right=mid? 偶区间的左边

区间右端点：mid=(right-left+1)/2+left? 因为left=mid? right=mid-1? 偶区间的右边

---

第三步：代码实现

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size()==0)
        {
            return {-1,-1};
        }
        int left=0,right=nums.size()-1;
        //取左端点值
        int begin=0;
        while(left<right)
        {
            int mid=(right-left)/2+left;
            if(nums[mid]<target)left=mid+1;
            else right=mid;
        }
        //判断是否有结果
        if(nums[left]!=target)return {-1,-1};
        else begin=left;

        //取右端点值
        left=0,right=nums.size()-1;
        while(left<right)
        {
            int mid=(right-left+1)/2+left;
            if(nums[mid]<=target)left=mid;
            else right=mid-1;
        }
        return {begin,left};
    }
};

---

第四步:总结模板

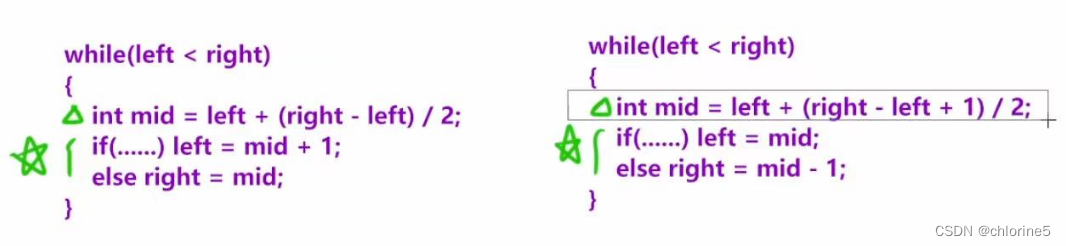
这只是初步的给个模板，后续会有题目来熟练认知这段代码。

---