3D数学--矢量

发布时间：2023年12月22日

矢量是具有大小和方向的有向线段

矢量大小（结果：标量）

||v|| = \sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}

矢量与标量乘法（结果：矢量）

kv=vk = (kv_{x},kv_{y},kv_{z})

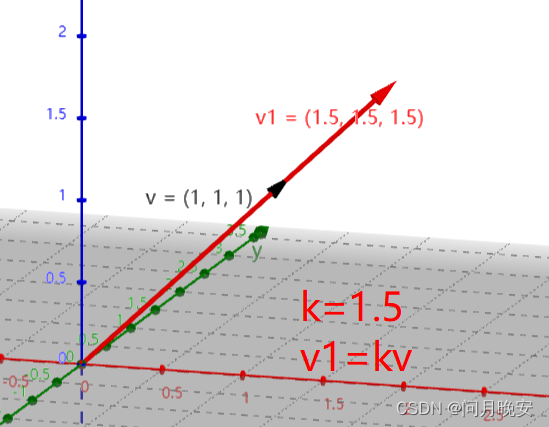
矢量加减法（结果：矢量）

????????

a\pm b=b\pm a = (a_{x}\pm b_{x},a_{y}\pm b_{y},a_{z}\pm b_{z})

矢量点积（结果：标量）

a\cdot b=b\cdot a=a_{x}b_{x} + a_{y}b_{y}+a_{z}b_{z}=\left | a \right |\left | b \right |cos\theta

1.矢量点积表示两个矢量的相似程度

2.若b为单位矢量，则a dot b为a在b方向上的投影

矢量叉积（结果：矢量）

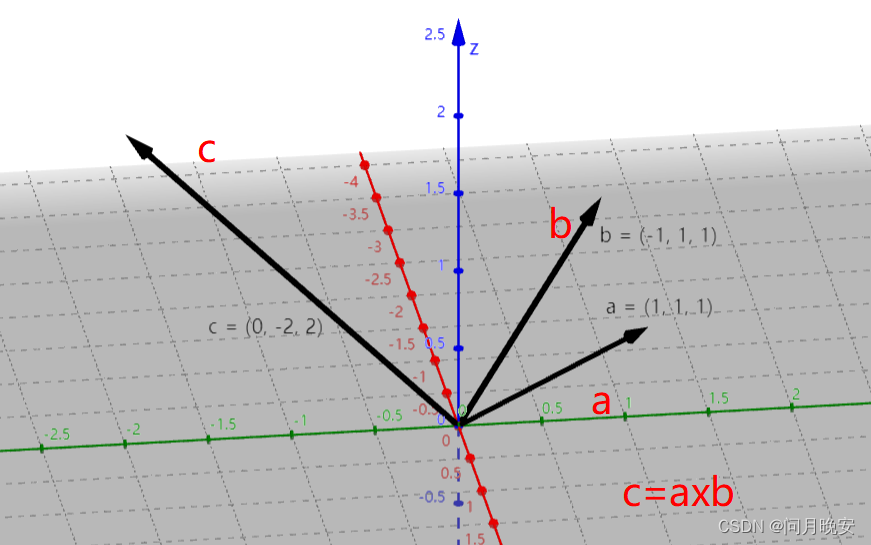
a\times b=\begin{bmatrix} a_{x}\\ a_{y}\\ a_{z}\\ \end{bmatrix}\times \begin{bmatrix} b_{x}\\ b_{y}\\ b_{z}\\ \end{bmatrix}=\begin{bmatrix} a_{y}b_{z}-a_{z}b_{y}\\ a_{z}b_{x}-a_{x}b_{z}\\ a_{x}b_{y}-a_{y}b_{x}\\ \end{bmatrix}=\left | a \right |\left | b \right |sin\theta

1.矢量叉积将产生一个矢量，此矢量垂直于原始的两个矢量

2.产生的新矢量方向遵循右手螺旋定则

文章来源:https://blog.csdn.net/a810373329/article/details/135159802
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章