python解决一维动态规划问题，寻找丑数

对于一维动态规划问题中，还有一个可能会经常遇到的问题，就是寻找丑数。

对于丑数的概念是，把只包含质因子2、3和5的数称作丑数（Ugly Number）。

添加图片注释，不超过 140 字（可选）

添加图片注释，不超过 140 字（可选）

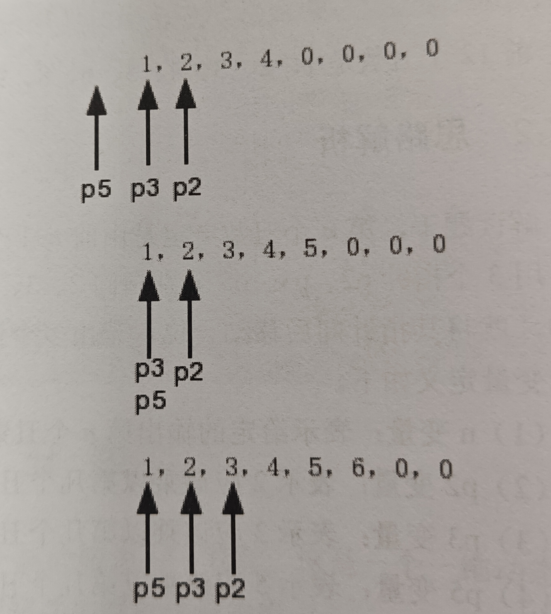
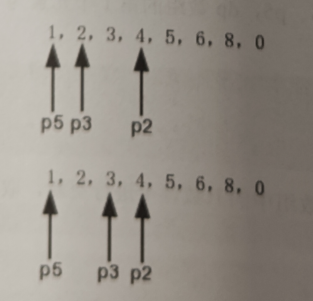
对于寻找丑数的问题，进行问题思路解读，主要是对于第n个丑数，前n-1个数中一定存在某三个丑数来分别乘以2,3,5，从职工取到的最小数就是这个第n个丑数，而对于这个思路，使用3个指针来分别代表乘以2,3,5的丑数，第n个丑数由那个指针得到的话，将该指针往后移动一位，如果说是由多个指针所指的丑数得到的，对应的指针都应该要后移一位。

添加图片注释，不超过 140 字（可选）

添加图片注释，不超过 140 字（可选）

添加图片注释，不超过 140 字（可选）

整个过程如上，其时间复杂度为O(n)，空间复杂度也很低，所以使用动态规划思路来解决该问题是非常高效的。

代码实现如下：

    def UglyNum(self, n):
        dp=[0]*n
        dp[0]=1
        p2=p3=p5=0
        for i in range(1,n):
            dp[i]=min(2*dp[p2],3*dp[p3],5*dp[p5])
            if dp[i]==2*dp[p2]:
                p2+=1
            if dp[i]==3*dp[p3]:
                p3+=1
            if dp[i]==5*dp[p5]:
                p5+=1
        return dp[-1]