BP神经网络（公式推导+举例应用）

引言

人工神经网络（Artificial Neural Networks，ANNs）作为一种模拟生物神经系统的计算模型，在模式识别、数据挖掘、图像处理等领域取得了显著的成功。其中，BP神经网络（Backpropagation Neural Network，BPNN）作为一种常见的前馈式神经网络，以其在模式学习和逼近函数方面的优越性受到广泛关注。BP神经网络不仅能够处理非线性关系，还能够通过训练不断调整网络参数，实现对复杂模型的逼近，具有较强的自适应性和泛化能力。

本文旨在深入探讨BP神经网络的基本原理和数学模型，通过对其公式的详细推导，为读者提供清晰的理论基础。此外，通过具体的举例应用，展示BP神经网络在实际问题中的有效性和应用前景。通过对BP神经网络的深入理解，我们可以更好地应用和优化该模型，推动人工智能领域的发展。

在神经网络研究的历史长河中，BP神经网络无疑是一个重要的里程碑，其不断演化和改进为解决实际问题提供了有力的工具。通过深入研究BP神经网络，我们有望更好地理解神经网络的内在机理，推动其在各个领域的广泛应用。在人工智能日益发展的今天，BP神经网络仍然是一个备受关注的研究方向，本文将为读者提供对其深入理解的途径和启发。

M-P神经元模型

在生物神经网络中，每个神经元与其他神经元相连接，当它“兴奋”时，就会向相连接的神经元发送化学物质，从而改变这些神经元内的电位；若某神经元的电位超过一个“阈值”，那么它就会被激活，即“兴奋”起来，向其他神经元发送化学物质。我们将上述所描述的情形抽象为下图所示（M-P神经元模型）：

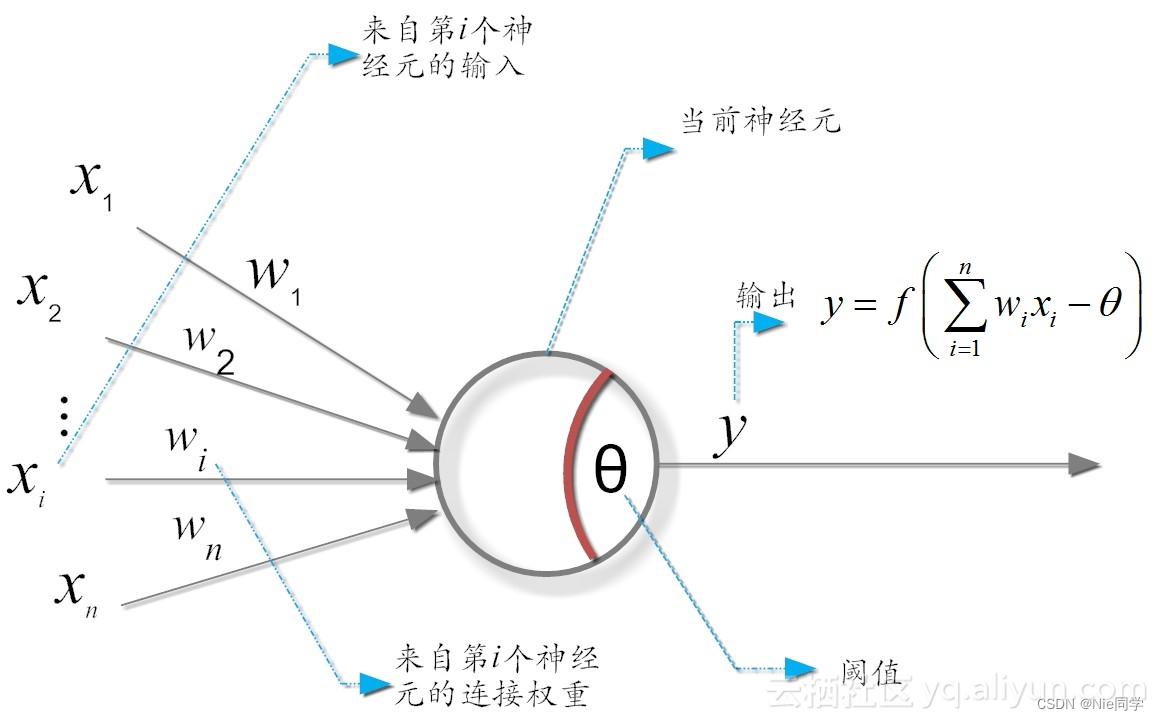
在这个模型中，神经元接受到来自$n$个其他神经元传递过来的输入信号，这些输入信号通过带权的连接进行传递，神经元接受到的总输入值与神经元的阈值进行对比，然后通过”激活函数“处理以产生神经元的输出。

激活函数

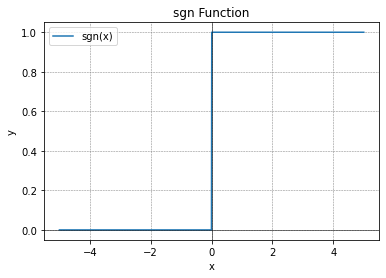
理想中的激活函数如下图所示：

$$sgn(x)=\{\begin{array}{l}1,x\ge 0\\ 0,x<0\end{array}$$
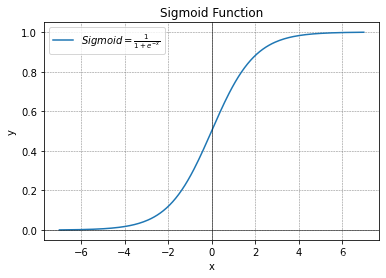
显然“1”对应神经元兴奋、“0”对应神经元抑制。然而$sgn(x)$数学性质不好，不具备连续性且不光滑。因此实际上我们采用$sigmoid$函数作为激活函数，典型的$sigmoid$函数如下图所示：

$$sigmoid(x)=\frac{1}{1+e^{?x}}$$
然后将许多的神经元按一定的层次连接起来，就构成了一个神经网络。

多层前馈神经网络

常见的神经网络是形如下图所示的层级结构：

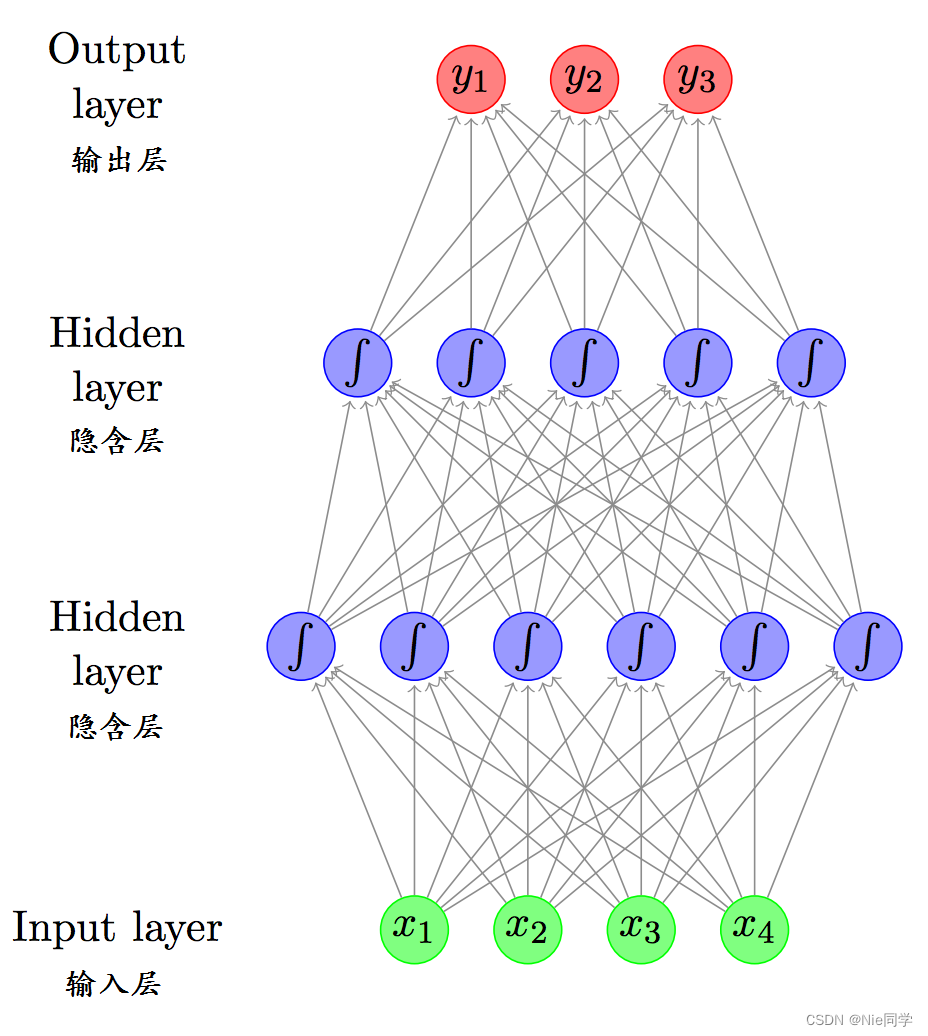
每层神经元与下一层神经元全连接，神经元之间不存在同层连接，也不存在跨层连接。这样的网络称为多层前馈神经网络。

误差逆传播算法

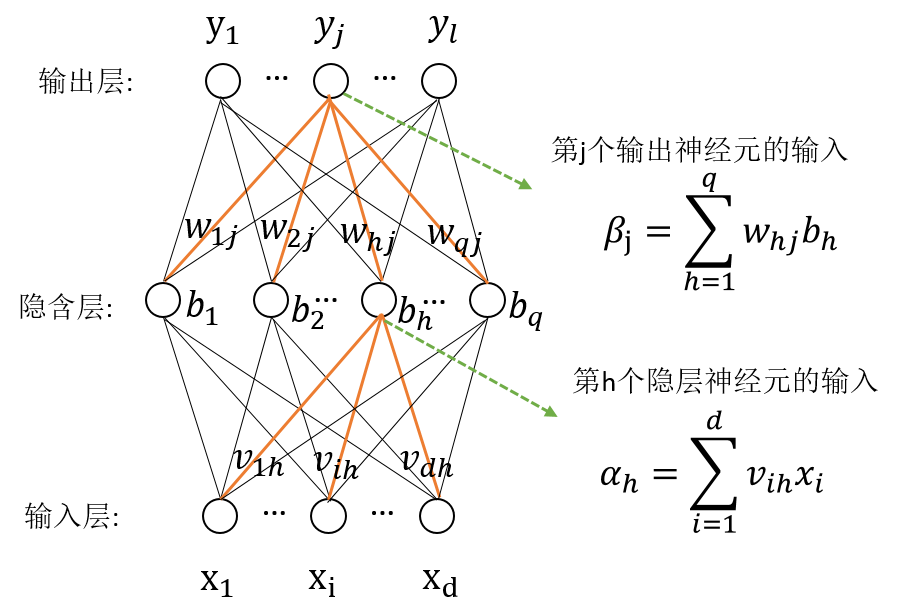
给定数据集$D=\{(x_1,y_1),(x_2,y_2),...(x_m,y_m)\}$，$x_i\in {?}^d,y_i\in {?}^l$，即输入样例由$d$个属性描述，输出样例由$l$维实值向量。下图给出一个拥有$d$个输入神经元、$l$个输出神经元、$q$个隐层神经元的多层前反馈神经网络。其中输出层第$j$个神经元的阈值用${\theta }_j$表示，隐层第$h$个神经元的阈值用${\gamma }_h$表示。输入层第$i$个神经元与隐层第$h$个神经元之间的连接权为$v_{ih}$，隐层第$h$个神经元与输出层第$j$个神经元之间的连接权为$w_{hj}$。记隐层第$h$个神经元接收到的输入为${\alpha }_h={\sum }_{i=1}^d{v}_{ih}{x}_i$，输出层第$j$个神经元接收到的输入为${\beta }_j={\sum }_{h=1}^q{w}_{hj}{b}_h$。其中$b_h$为隐层第$h$个神经元的输出。

对训练集$(x_k,y_k)$，假定神经网络的输出为${\hat{y}}_j^k=({\hat{y}}_1^k,{\hat{y}}_1^k,...,{\hat{y}}_l^k)$即
$${\hat{y}}_j^k=f({\beta }_j?{\theta }_j)\text{\hspace{1em}(1)}$$
则网络在$x_k,y_k$上的均方误差为：
$$E_k=\frac{1}{2}\sum _{j=1}^l({\hat{y}}_j^k?y_j^k{)}^2\text{\hspace{1em}(2)}$$
其中${\hat{y}}_j^k$为神经网络模型输出，$y_j^k$为训练集实际样例输出。

故在上图网络中共有$(d+l+1)q+l$个参数。BP是一个迭代学习算法，在迭代的每一轮中采用广义感知机学习规则对参数进行更新估计，任意参数$v$的更新估计式为：
$$v\leftarrow v+\Delta v\text{\hspace{1em}(3)}$$

以上图的BP网络中隐层到输出层的连接权$w_{hj}$为例来进行推导：
BP算法基于梯度下降法，以目标的负梯度方向对参数进行调整，对误差$E_k$，给定学习率$\eta$，有：
$$\Delta w_{hj}=?\eta \frac{?E_k}{?w_{hj}}\text{\hspace{1em}(4)}$$
我们注意到$w_{hj}$先影响到第$j$个输出层神经元的输入值${\beta }_j$，再影响到输出值${\hat{y}}_j^k$，最终影响到$E_k$，有：
$$\frac{?E_k}{?w_{hj}}=\frac{?E_k}{?{\hat{y}}_j^k}?\frac{?{\hat{y}}_j^k}{?{\beta }_j}?\frac{?{\beta }_j}{?w_{hj}}\text{\hspace{1em}(5)}$$

根据${\beta }_j={\sum }_{h=1}^q{w}_{hj}{h}_h$的定义，显然有：
$$\frac{?{\beta }_j}{?w_{hj}}=b_h\text{\hspace{1em}(6)}$$

又因为$sigmoid$函数有一个很好的数学性质：
$$f^{\prime }(x)=f(x)(1?f(x))\text{\hspace{1em}(7)}$$

根据式子(1)和(2)，有：
$$\begin{array}{rl}{g}_j& =?\frac{?E_k}{?{\hat{y}}_j^k}?\frac{?{\hat{y}}_j^k}{?{\beta }_j}\\ & =?({\hat{y}}_j^k?y_j^k)f^{\prime }({\beta }_j?{\theta }_j)\\ & ={\hat{y}}_j^k(1?{\hat{y}}_j^k)(y_j^k?{\hat{y}}_j^k)\end{array}\text{\hspace{1em}(8)}$$
其中$E_k=\frac{1}{2}{\sum }_{j=1}^l({\hat{y}}_j^k?y_j^k{)}^2$，那么$\frac{?E_k}{?{\hat{y}}_j^k}={\hat{y}}_j^k?y_j^k$。${\hat{y}}_j^k=f({\beta }_j?{\theta }_j)$，那么$\frac{?{\hat{y}}_j^k}{?{\beta }_j}=f^{\prime }({\beta }_j?{\theta }_j)=f({\beta }_j?{\theta }_j)?(1?f({\beta }_j?{\theta }_j))={\hat{y}}_j^k?(1?{\hat{y}}_j^k)$

将（6）和（8）带入（5）中有：
$$\frac{?E_k}{?w_{hj}}=g_j?b_h\text{\hspace{1em}(9)}$$

再将（9）带入（4）中，得到BP算法 中关于$w_{hj}$的更新公式：
$$\Delta w_{hj}=?\eta g_j{b}_h\text{\hspace{1em}(10)}$$

同理可得：
$$\Delta {\theta }_j=?\eta g_j\text{\hspace{1em}(11)}$$
$$\Delta v_{ih}=\eta e_h{x}_i\text{\hspace{1em}(12)}$$
$$\Delta {\gamma }_h=?\eta e_h\text{\hspace{1em}(13)}$$
其中
$$\begin{array}{rl}{e}_h& =?\frac{?E_k}{?b_h}?\frac{?b_h}{?{\alpha }_h}\\ & =?\sum _{j=1}^l\frac{?E_k}{?{\beta }_j}?\frac{?{\beta }_j}{?b_h}{f}^{\prime }({\alpha }_h?{\gamma }_h)\\ & =\sum _{j=1}^l{w}_{hj}{g}_j{f}^{\prime }({\alpha }_h?{\gamma }_h)\\ & =b_h(1?b_h)\sum _{j=1}^l{w}_{hj}{g}_j\end{array}\text{\hspace{1em}(14)}$$

其中$b_h$是隐层神经元的输出$b_h=f({\alpha }_h?{\gamma }_h)$，${\gamma }_h$是隐层神经元的阈值，${\alpha }_h$是隐层神经元的输入。
直到所有参数调整至累计误差最小即：
$$E_{min}=\frac{1}{m}\sum _{k=1}^m{E}_k\text{\hspace{1em}(15)}$$

缓解过拟合化

由于BP神经网络强大的表示能力，BP神经网络经常遭遇过拟合化，其训练误差持续降低，但测试误差却可能上升。共有两种策略来缓解BP网络的过拟合化。

• 早停：基本思想是在训练过程中监测验证集（一部分未参与训练的数据）上的性能，并在验证集性能达到最优时停止训练，而不是继续训练直到训练误差降为零。
• 正则化：正则化通过修改损失函数，向优化过程中引入额外的惩罚项，从而限制模型的复杂性。这有助于防止神经网络对训练数据过度拟合。在神经网络中，L2（范数） 正则化的损失函数，则误差目标函数为：
  $$E=\lambda \frac{1}{m}\sum _{k=1}^m{E}_k+(1?\lambda )\sum _i{w}_i^2\text{\hspace{1em}(16)}$$
  其中$\lambda \in (0,1)$，用来对经验风险和结构风险进行折中处理。其中经验风险为$\frac{1}{m}{\sum }_{k=1}^m{E}_k$，结构风险为${\sum }_i{w}_i^2$。

结论

在神经网络领域，BP神经网络是一种重要的前馈神经网络，以其在模式学习和逼近函数方面的优越性而备受关注。本文深入探讨了BP神经网络的基本原理和数学模型，通过对其公式的详细推导，为读者提供了清晰的理论基础。

文章首先介绍了M-P神经元模型，将其抽象为神经网络的基本组成单元。激活函数的选择是神经网络设计中关键的一步，文中提到了理想中的激活函数以及实际中常用的$sigmoid$函数。

多层前馈神经网络的结构被详细介绍，说明了其层级结构和连接方式。这种结构的神经网络被广泛应用于各个领域，能够处理非线性关系，通过训练调整网络参数，实现对复杂模型的逼近，具有较强的自适应性和泛化能力。

误差逆传播算法是BP神经网络训练的核心，文章通过数学推导详细解释了权重和阈值的更新过程。梯度下降法是其中的关键步骤，通过计算误差对参数的偏导数，实现对参数的调整。

然后，文章提到了BP神经网络容易面临的问题之一，即过拟合。为了缓解过拟合，介绍了两种常用的方法：早停和正则化。早停通过在训练过程中监测验证集性能，及时停止训练，避免过度拟合。正则化通过修改损失函数引入额外的惩罚项，限制模型复杂性，有助于防止神经网络对训练数据过度拟合。

实验分析

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# 读入数据集
data = pd.read_csv('data/predict_room_price.csv')

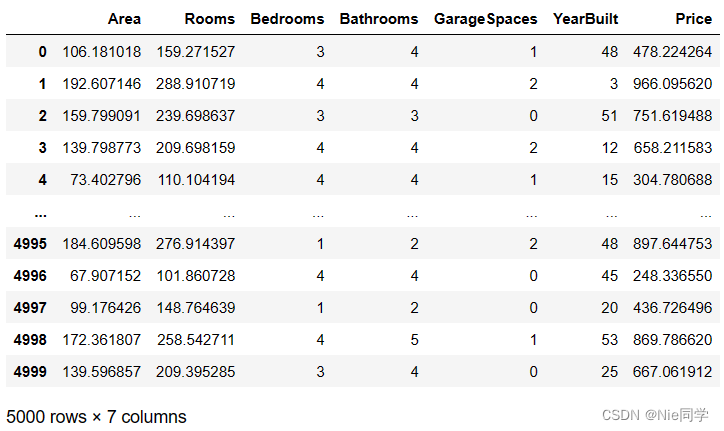
进行数据的预处理

# 特征和标签
X = data.drop('Price', axis=1)
y = data['Price']

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 划分数据集
X_train, X_temp, y_train, y_temp = train_test_split(X_scaled, y, test_size=0.3, random_state=42)
X_valid, X_test, y_valid, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)

构建神经网络模型

# 创建BP神经网络模型
model = MLPRegressor(hidden_layer_sizes=(20, 20), max_iter=1000, random_state=42, alpha=0.01, learning_rate='adaptive')

训练、预测并评估模型性能

# 训练模型
model.fit(X_train, y_train)

# 在验证集上预测
y_valid_pred = model.predict(X_valid)


# 评估模型性能
valid_loss = mean_squared_error(y_valid, y_valid_pred)
print(f'Validation Loss: {valid_loss}')

# 在测试集上预测
y_test_pred = model.predict(X_test)

# 评估模型性能
test_loss = mean_squared_error(y_test, y_test_pred)
print(f'Test Loss: {test_loss}')

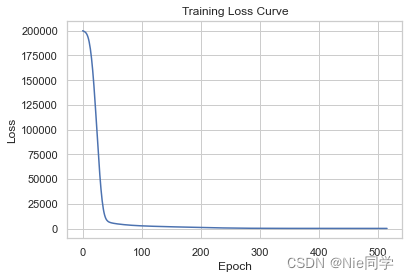
# 绘制损失曲线
plt.plot(model.loss_curve_)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Curve')
plt.show()

Validation Loss: 429.78130878683345
Test Loss: 436.7118813730095

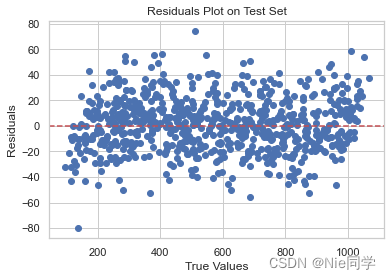
residuals = y_test - y_test_pred
plt.scatter(y_test, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('True Values')
plt.ylabel('Residuals')
plt.title('Residuals Plot on Test Set')
plt.show()

from sklearn.metrics import r2_score

r2_valid = r2_score(y_valid, y_valid_pred)
print(f'R2 Score on Validation Set: {r2_valid}')

r2_test = r2_score(y_test, y_test_pred)
print(f'R2 Score on Test Set: {r2_test}')

R2 Score on Validation Set: 0.9939169086519464
R2 Score on Test Set: 0.9934083540996065

由上述评价指标可知：

• 残差图：

  • 散点在区间[-80, 80]内，说明模型的预测相对较为准确，大多数样本的预测误差在这个范围内。
  • 点集中在[-20, 20]上，表示大部分样本的残差（实际值与预测值之差）都集中在这个范围内，这也表明模型的整体性能较好。

• Validation Loss 和 Test Loss：非常低的Validation Loss和Test Loss，说明模型在验证集和测试集上都取得了很好的性能。这表明模型对数据的拟合效果很好，预测值与实际值之间的误差很小。

• R2 Score on Validation Set 和 Test Set：非常接近于1的R2 Score，表明模型对于验证集和测试集的解释方差非常高。R2 Score是一个用于评估模型拟合程度的指标，接近1表示模型能够很好地解释目标变量的变异性。

总体来说，根据残差图、Validation Loss、Test Loss以及R2 Score的结果，模型表现出色，能够很好地拟合数据并具有较高的泛化能力。