01--二分查找

发布时间：2023年12月17日

一. 初识算法

1.1 什么是算法？

在数学和计算机科学领域，算法是一系列有限的严谨指令，通常用于解决一类特定问题或执行计算

不正式的说，算法就是任何定义优良的计算过程：接收一些值作为输入，在有限的时间内，产生一些值作为输出。

1.2 什么是数据结构？

在计算机科学领域，数据结构是一种数据组织、管理和存储格式，通常被选择用来高效访问数据

数据结构是一种存储和组织数据的方式，旨在便于访问和修改

1.3 衡量算法好坏

一般从以下维度来评估算法的优劣：正确性、可读性、健壮性（对不合理输入的反应能力和处理能力）。
时间复杂度（time complexity）：估算程序指令的执行次数（执行时间）。
空间复杂度（space complexity）：估算所需占用的存储空间。

1.3.1 时间复杂度

常见的时间复杂度从快到慢：

常数复杂度 ????????????????????????????????O(1)

对数复杂度 ????????????????????????????????O(logn)

线性时间复杂度 ?????????????????????????O(n)

线性对数复杂度? ? ? ? ? ? ? ? ? ? ? ? ? O(nlogn)

平方 ???????????????????????????????????????????O(n^{2})

立方? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? O(n^{3})

指数? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? O(2^{n})

阶乘 ???????????????????????????????????????????O(n!)

1.3.2 空间复杂度

空间复杂度就是算法需要多少内存，占用了多少空间

常用的空间复杂度有O(1)、O(n)、O(n^{2})

二、二分查找

二分查找算法也称折半查找，是一种非常高效的工作于有序数组的查找算法。

2.1 二分查找基础版

	/**
     * @description: 二分查找基础版
     * @author: 憨憨浩浩
     * @date: 2023/12/11 21:54
     * @param: [a, target]
     * @return: int
     **/
    public static int binarySearchBasic(int[] a, int target) {
        // 定义左侧指针
        int i = 0;
        // 定义右侧指针
        int j = a.length - 1;
        // 当 i > j 时退出循环
        while (i <= j){
            // 定义中间指针
            int m = (i + j) / 2;
            if (a[m] > target){     // 目标值在左边
                j = m - 1;
            }else if (a[m] < target){       // 目标值在右边
                i = m + 1;
            }else {     // 找到目标值返回对应索引
                return m;
            }
        }
        return -1;      // 找不到目标值返回-1
    }

(i + j) / 2 有没有问题?

有问题，当数组长度足够长是会发生问题；

	@Test
    public void Test01(){
        int i = Integer.MAX_VALUE / 2;
        int j = Integer.MAX_VALUE;
        int m = (i + j) / 2;
        System.out.println(m);		// -536870913
    }

解决方案：

	@Test
    public void Test02(){
        int i = Integer.MAX_VALUE / 2;
        int j = Integer.MAX_VALUE;
        int m = (i + j) >>> 2;
        System.out.println(m);		// 805306367
    }

2.2 二分查找改变版

另一种写法

	/**
     * @description: 二分查找改变版
     * @author: 憨憨浩浩
     * @date: 2023/12/11 22:10
     * @param: [a, target]
     * @return: int
     **/
    public static int binarySearchAlternative(int[] a,int target){
        // 定义左侧指针
        int i = 0;
        // 定义右侧指针
        int j = a.length;
        // 当 i = j 时退出循环
        while (i < j){
            // 定义中间指针
            int m = (i + j) /2;
            if (a[m] > target){     // 目标值在左边
                j = m;
            } else if (a[m] < target) {     // 目标值在右边
                i = m + 1;
            }else {     // 找到目标值返回对应索引
                return m;
            }
        }
        return -1;      // 找不到目标值返回-1
    }

2.3 二分查找性能

2.4 二分查找平衡版

	/**
     * @description: 二分查找平衡版
     * @author: 憨憨浩浩
     * @date: 2023/12/13 13:46
     * @param: [a, target]
     * @return: int
     **/
    public static int binarySearchBalance(int[] a,int target){
        // 定义左侧指针
        int i = 0;
        // 定义右侧指针
        int j = a.length;
        // 当 i + 1 > j 时退出循环
        while (1 < j - i) {
            // 定义中间指针
            int m = (i + j) >>> 1;
            if (target < a[m]) {     // 目标值在左边
                j = m;
            } else {
                i = m;
            }
        }
        // 查到返回i，查不到返回-1
        return (a[i] == target) ? i : -1;
    }

2.5 二分查找 Java 版

Java8源码：

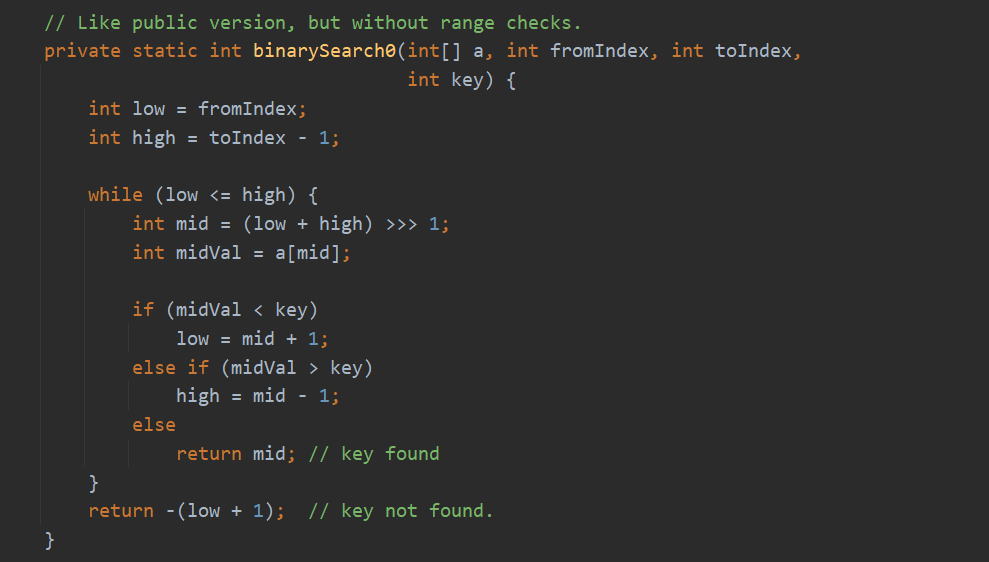
public static int binarySearch(int[] a, int key) {
        return binarySearch0(a, 0, a.length, key);
    }


private static int binarySearch0(int[] a, int fromIndex, int toIndex, int key) {
        int low = fromIndex;
        int high = toIndex - 1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            int midVal = a[mid];

            if (midVal < key)
                low = mid + 1;
            else if (midVal > key)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found.
    }

2.6 Leftmost 与 Rightmost

	/**
     * @description: 二分查找返回左侧的索引值
     * @author: 憨憨浩浩
     * @date: 2023/12/15 20:21
     * @param: [a, target]
     * @return: int
     **/
    public static int binarySearchLeftmost1(int[] a,int target){
        int i = 0, j = a.length - 1;
        int candidate = -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                candidate = m; // 记录候选位置
                j = m - 1;     // 继续向左
            }
        }
        return candidate;
    }

如果希望返回的是最右侧元素

	/**
     * @description: 二分查找返回最右侧值的索引
     * @author: 憨憨浩浩
     * @date: 2023/12/15 20:23
     * @param: [a, target]
     * @return: int
     **/
    public static int binarySearchRightmost1(int[] a,int target){
        int i = 0, j = a.length - 1;
        int candidate = -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                candidate = m; // 记录候选位置
                i = m + 1;	   // 继续向右
            }
        }
        return candidate;
    }

应用

对于 Leftmost 与 Rightmost，可以返回一个比 -1 更有用的值

Leftmost 改为

public static int binarySearchLeftmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target <= a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i; 
}

Rightmost 改为

public static int binarySearchRightmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i - 1;
}

大于等于中间值，都要向右找

几个名词

?

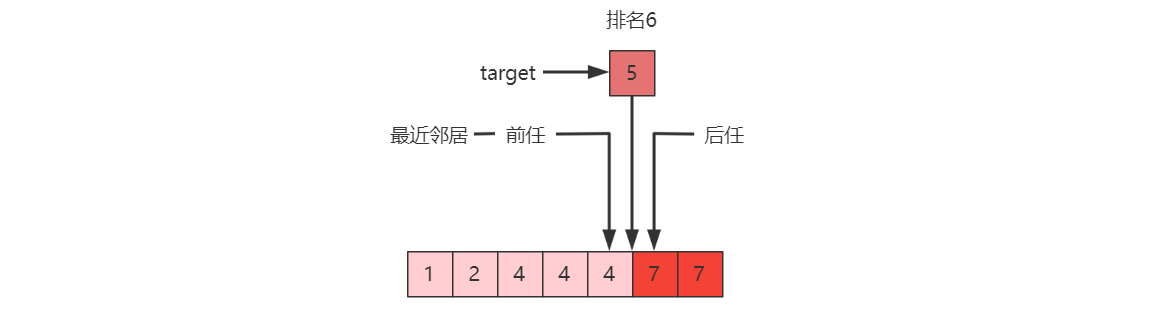
文章来源:https://blog.csdn.net/weixin_46612641/article/details/135049996
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章