图论相关基本概念
发布时间:2024年01月12日
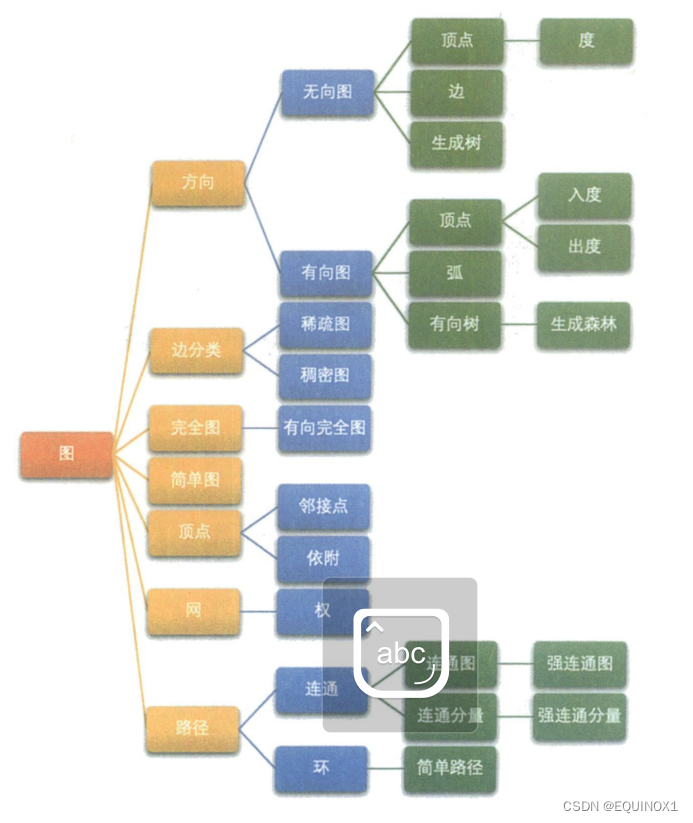
图的基本概念
从逻辑结构上讲,图是一种典型的非线性结构。
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成的,通常表示为 G(V , E) ,其中, G表示—个图,V是图G中顶点的集合,E是图G中边的集合。其中:
顶点集合V={x|x属于某个数据对象集}是有穷非空集合
E={(x,y)|x,y属于V&&Path(x,y)}是顶点间关系的有穷集合,也叫做边的集合。
有向边和无向边
若顶点x到y之间的边没有方向则称这条边为无向边(Edge),用**无序偶对(x,y)**来表示
若顶点x到y之间的边有方向则称这条边为有向边,也称为弧(Arc)。连接顶点x到y的有向边就是弧,x是弧尾,y是弧头,用<x,y>来表示
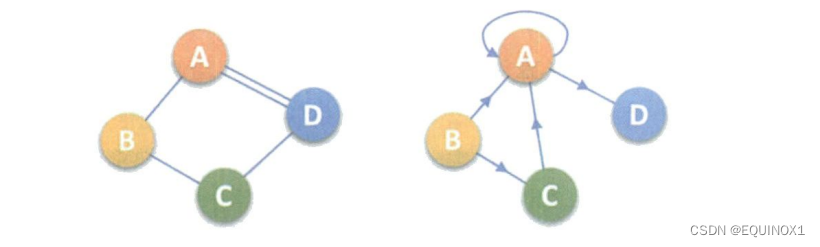
简单图
在图中,若不存在顶点到自身的边,且同一条边不重复出现则称这样的图为简单图。
如下两个图就不是简单图
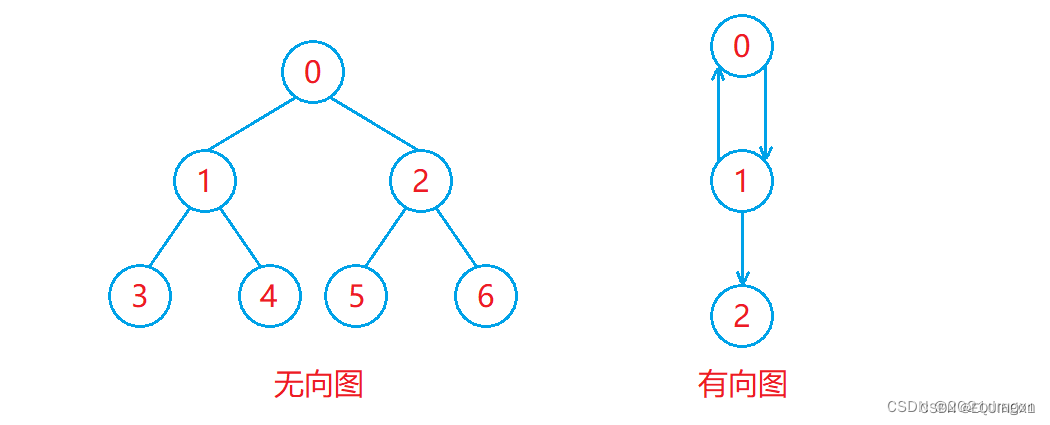
有向图和无向图
- 在有向图中,顶点对 < x , y > <x, y><x,y> 是有序的,顶点对 < x , y > <x, y><x,y> 称为顶点 x 到顶点 y 的一条边(弧),< x , y > <x, y> 和 < y , x > 是两条不同的边。
- 在无向图中,顶点对 ( x , y ) 是无序的,顶点对 ( x , y ) 称为顶点 x 和顶点 y 相关联的一条边,这条边没有特定方向,( x , y ) 和 ( y , x ) 是同一条边。
如下图:
完全图
- 在有 n 个顶点的无向图中,若有 n * ( n ? 1 ) / 2 条边,即任意两个顶点之间都有直接相连的边,则称此图为无向完全图。
- 在有 n 个顶点的有向图中,若有 n × ( n ? 1 ) 条边,即任意两个顶点之间都有双向的边,则称此图为有向完全图。
如下图

稀疏图和稠密图
有很少条边或弧的图称为稀疏图,反之称为稠密图。
邻接顶点:
- 在无向图中,若 ( u , v ) 是图中的一条边,则称 u 和 v 互为邻接顶点,并称边 ( u , v ) 依附于顶点 u 和顶点 v 。
- 在有向图中,若 < u , v > 是图中的一条边,则称顶点 u 邻接到顶点 v,顶点 v 邻接自顶点 u ,并称边 < u , v > 与顶点 u和顶点 v 相关联。
顶点的度:
- 在有向图中,顶点的度等于该顶点的入度与出度之和,顶点的入度是以该顶点为终点的边的条数,顶点的出度是以该顶点为起点的边的条数。
- 在无向图中,顶点的度等于与该顶点相关联的边的条数,同时也等于该顶点的入度和出度。
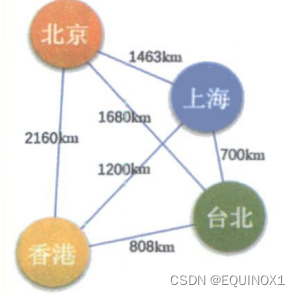
权
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权( Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网( Network)。
下图就是-一张带权的图,即标志中国四大城市的直线距离的网,此图中的权就是两地的距离。
路径与路径长度:
- 若从顶点 vi 出发有一组边使其可到达顶点 vj ,则称顶点 vi 到顶点 vj的顶点序列为从顶点 vi 到顶点 vj的路径。
- 对于不带权的图,一条路径的长度是指该路径上的边的条数;对于带权的图,一条路径的长度是指该路径上各个边权值的总和。
简单路径与回路
- 若路径上的各个顶点均不相同,则称这样的路径为简单路径。
- 若路径上第一个顶点与最后一个顶点相同,则称这样的路径为回路或环。

子图
- 设图 G = ( V , E ) 和图 G 1 = ( V1 , E1 ) ,若 V1 ? V 且 E1 ? E ,则称 G1 是 G 的子图。
如下图: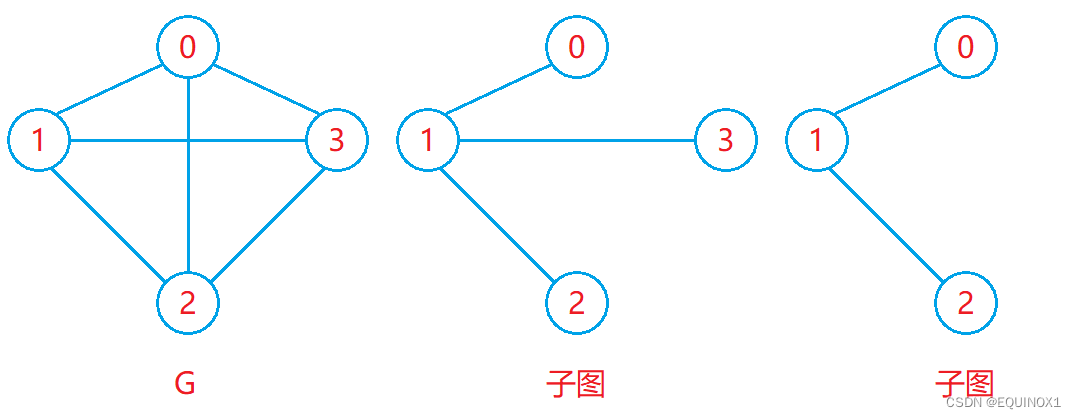
连通图和强连通图
- 在无向图中,若从顶点 v1到顶点 v2有路径,则称顶点 v1与顶点 v2 是连通的,如果图中任意一对顶点都是连通的,则称此图为连通图。
- 在有向图中,若每一对顶点 vi 和 vj 之间都存在一条从 vi 到 vj 的路,也存在一条从 vj到 vi 的路,则称此图是强连通图。
连通分支
无向图中的极大连通子图称为连通分支,注意:
- 要是子图
- 子图是连通的
- 连通子图含有极大顶点数
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边
例如下图中,图2图3是图1的两个连通分支,但是图四却不是,因为不是极大连通子图

生成树与最小生成树
- 一个连通图的最小连通子图称为该图的生成树,有 n 个顶点的连通图的生成树有 n个顶点和 n ? 1条边。
- 最小生成树指的是一个图的生成树中,总权值最小的生成树。
有向树
如果一个有向图恰有一个顶点的入度为0,其余顶点的入度均为1,则是一个有向树
生成森林
一个有向图的生成森林由若干棵有向树组成, 含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧
文章来源:https://blog.csdn.net/EQUINOX1/article/details/135541031
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Hive实战:词频统计
- word的docx模板导出,poi
- JOSEF约瑟 温度继电器 JUC-1M (≥20℃断开)常开型
- 文件\学生信息录入
- 基于springboot+vue的java宿舍管理系统
- 获取 Linux 系统中所有网络命名空间的路由表
- java-集合框架
- 二、类加载、连接和初始化
- asp.net core 教程
- 基于多反应堆的高并发服务器【C/C++/Reactor】(中)Dispatcher模块的实现思路