读书笔记-算法图解(像小说一样有趣的算法入门书)
作者:[美] Aditya Bhargava
什么时候读本书:
面临一个编程问题,需要找一种算法来实现解决方案,或你想知道哪些算法比较有用。
本书特点:结合生活中的场景来讲算法
问题解决技巧,遇到问题不确定应该如何解决,可以尝试分而治之或者动态规划;如果认识到根本就没有高校的解决方案,可以转而采用贪婪算法来得到近似答案(比如NP完全问题)
每当我需要解决问题时,首先想到的两种方法是:可以使用散列表吗?可以使用图来创建模型吗
广度优先搜索和狄克斯特拉算法计算网络中两点之间的最短距离,可用来计算两人之间的分隔度或前往目的地的最短路径。GPS设备使用图算法来计算前往目的地的最短路径。
可使用动态规划来编写下国际跳棋的AI算法。
K最近邻算法(KNN):是一种简单的机器学习算法,可用于创建推荐系统、OCR发动机、预测股价或其他值(如“我们认为Adit会给这部电影打4星”)的系统,以及对物件进行分类(如“这个字母是Q”)
算法的代码例子(代码都是使用Python 2.7)
https://github.com/egonschiele/grokking_algorithms
1 算法简介
二分查找的速度比简单查找快得多。
二分查找的小游戏:
我在1-100中想一个数字,你猜,我告诉你大了或者小了或者正确。
O(log n)比O(n)快。需要搜索的元素越多,前者比后者就快得越多。
算法运行时间并不以秒为单位。
算法运行时间是从其增速的角度度量的。
算法运行时间用大O表示法表示。
2 数据结构
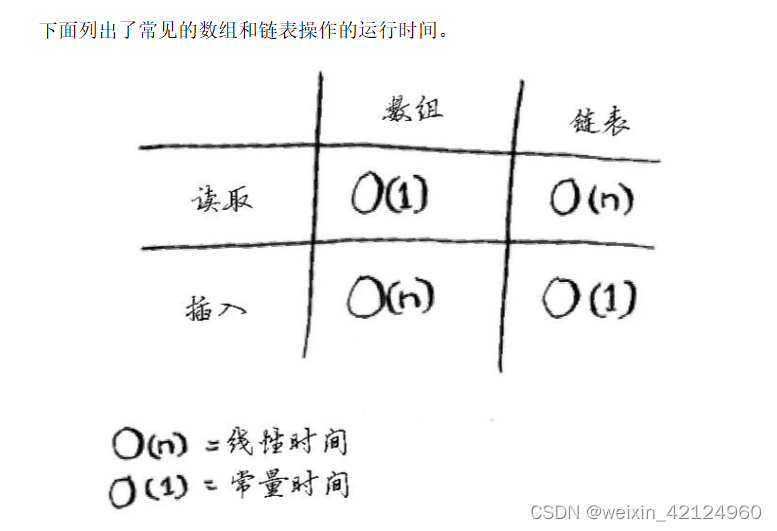
散列表
学习散列表的内部机制:实现、冲突和散列函数。这将帮助你理解如何分析散列表的性能
结合使用散列函数和数组创建了一种被称为散列表(hash table)的数据结构。散列表是你学习的第一种包含额外逻辑的数据结构。数组和链表都被直接映射到内存,但散列表更复杂,它使用散列函数来确定元素的存储位置。
也被称为散列映射、映射、字典和关联数组。散列表由键和值组成。
散列表适合用于:
仿真映射关系;
防止重复;
缓存/记住数据,以免服务器再通过处理来生成它们
要避免冲突,需要有:
较低的填装因子;一个不错的经验规则是:一旦填装因子大于0.7,就调整散列表的长度。
良好的散列函数。
3 选择排序
选择排序比较慢,找到列表中最小元素,放到新的数组中
4 递归
如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。
递归指的是调用自己的函数。
每个递归函数都有两个条件:基线条件和递归条件。
栈有两种操作:压入和弹出。
所有函数调用都进入调用栈。
调用栈可能很长,这将占用大量的内存
存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存,如果栈很高,就意味着计算机存储了大量函数调用的信息。在这种情况下,你有两种选择。
重新编写代码,转而使用循环
5 快速排序-分而治之
原理:
(1) 找出简单的基线条件;
(2) 确定如何缩小问题的规模,使其符合基线条件
在基线条件中,我证明这种算法对空数组或包含一个元素的数组管用。在归纳条件中,我证明如果快速排序对包含一个元素的数组管用,对包含两个元素的数组也将管用;如果它对包含两个元素的数组管用,对包含三个元素的数组也将管用。
代码python:
def quick(self,list):
if len(list) < 2:
return list; #基线条件:为空或只包含一个元素的数组是“有序”的
else:
pivot = list[0] #递归条件
less =[i for i in list[1:] if i <= pivot ] #由所有小于基准值的元素组成的子数组
greater = [i for i in list[1:] if i > pivot] #由所有大于基准值的元素组成的子数组
return self.quick(less) + [pivot] + self.quick(greater)
广度优先搜索
使用狄克斯特拉
贪婪算法
动态规划
K最近邻算法
树
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 09-Pub/Sub
- 4.CentOS7开启ssh
- springboot切面怎么将参数修改后传给目标方法
- 平衡小车——调试协议
- 方案:在 Linux 上将 Jira or Confluence 作为 systemd 服务运行
- Windows 截图工具①FastStone Capture ②PixPin
- 人工智能导论复习资料
- [c++学习打卡]STL
- 全志T113开发板Qt远程调试
- [R] Importing, viewing and screening imported data