【提示学习论文五】Conditional Prompt Learning for Vision-Language Models论文原理及复现工作
Conditional Prompt Learning for Vision-Language Models 视觉语言模型的条件提示学习
文章介绍
- 这篇文章于2022年发表在CVPR(Conference on Computer Vision and Pattern Recognition),作者是kaiyang.zhou, jingkang001, ccloy, ziwei.liu。
- 研究发现CoOp的问题:泛化性差,CoOp在训练时对于已知类别(base classes)过拟合,学习的上下文向量不能推广到同一数据集中的未知类。
- 作者提出Conditional Context Optimization(CoCoOp)。CoCoOp在CoOp基础上引入一个轻量级的神经网络为每张图像生成 input-conditional tokens(vectors),这些tokens会加到原本CoOp的learnable vectors上,从而可以学习到更泛化的prompt。
问题背景

- CoOp是一种有效利用数据的方法,只需少量标记图像数据即可训练上下文向量,以提高模型性能。
- 然而,CoOp存在一个问题,其学到的上下文信息无法推广到同一数据集中更广泛的未知类别,CoOp在训练中过于专注于特定类别,导致模型无法很好地泛化到其他类别上。
- 作者认为,通过实例条件化上下文,可以更好地泛化,因为这使得模型不再专注于特定一组类别,而是关注于每个输入实例及整个任务。
- 为了解决这个问题,提出了CoCoOp方法。
设计
- 简单实现方法: 构建 M M M个神经网络来生成 M M M个上下文标记,但这会增加计算资源的需求。
- 参数效率设计: 作者提出了更高效的设计方案,该方案在M个上下文向量的基础上进一步学习一个轻量级的神经网络(Meta-Net)。这个Meta-Net用于为每个输入图像生成一个条件化的标记,并将其与上下文向量结合。
模型结构
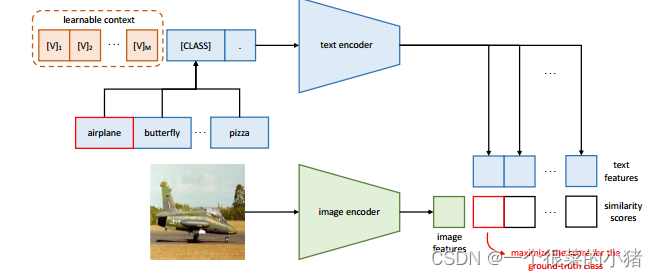
- CoOp
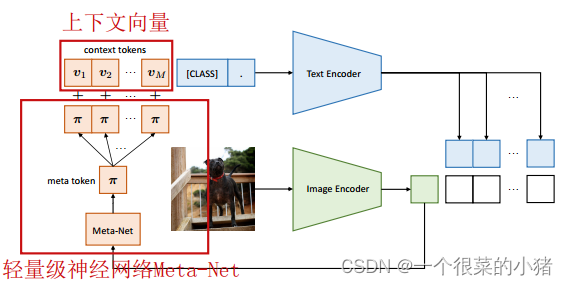
- CoCoOp:由两个可学习的组件组成,一组上下文向量和一个轻量级神经网络(Meta-Net),为每个图像生成一个输入条件token
- 输入图像编码器生成的图像 x \mathbf{x} x 特征 ,通过 Meta-Net 生成相应的条件标记 t y ( x ) \mathbf{t}_y (\mathbf{x}) ty?(x)
- 计算输入图像 x \mathbf{x} x 与每个类别提示 t i ( x ) \mathbf{t}_i (\mathbf{x}) ti?(x)之间的相似度
- 对于每个类别 i i i ,将相似度值作为指数项应用于指数函数,同时用温度参数 τ \tau τ 进行缩放,将相似度映射为概率得分
- 将所有类别的指数项相加并归一化,得到每个类别的归一化概率分布
- 最终的预测概率表示为给定输入图像 x \mathbf{x} x下属于每个类别的可能性。
实现细节
p ( y ∣ x ) = exp ? ( sim ? ( x , g ( t y ( x ) ) ) / τ ) ∑ i = 1 K exp ? ( sim ? ( x , g ( t i ( x ) ) / τ ) p(y | \mathbf{x}) = \frac{\exp (\operatorname{sim} (\mathbf{x}, g(\mathbf{t}_y (\mathbf{x}))) / \tau )}{\sum_{i=1}^K \exp (\operatorname{sim} (\mathbf{x}, g(\mathbf{t}_i (\mathbf{x})) / \tau )} p(y∣x)=∑i=1K?exp(sim(x,g(ti?(x))/τ)exp(sim(x,g(ty?(x)))/τ)?
-
计算预测概率的公式,涉及了上下文标记和模型的预测函数。
-
评估模型对给定输入图像的类别预测概率。
-
训练过程中,更新了上下文向量 v m {v_m} vm? 和 Meta-Net 的参数 θ θ θ 。
-
Meta-Net 结构: Meta-Net采用了一个两层的瓶颈结构,隐藏层将输入维度降低了16倍。
参数
- p ( y ∣ x ) p(y | \mathbf{x}) p(y∣x):表示在给定输入图像 x \mathbf{x} x 的情况下,模型预测为类别 y y y 的概率。
- t y ( x ) \mathbf{t}_y (\mathbf{x}) ty?(x):表示输入图像 x \mathbf{x} x 对应类别 y y y 的提示(即条件化的标记),包括了关于这个图像的特定信息。
- sim ? ( x , g ( t i ( x ) ) ) \operatorname{sim} (\mathbf{x}, g(\mathbf{t}_i (\mathbf{x}))) sim(x,g(ti?(x))):表示图像 x \mathbf{x} x 与类别 i i i的提示 t i ( x ) \mathbf{t}_i (\mathbf{x}) ti?(x)之间的相似度。这个相似度函数可以是任何测量图像与提示之间相似程度的函数。
- K K K:表示类别的总数。
- τ \tau τ:表示温度参数,用于调整预测分布的平滑度。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 楼宇管理新智慧:Panorama SCADA楼宇管理系统应用实例
- GEE报错:Request payload size exceeds the limit: 10485760 bytes.
- LeetCode 1758. 生成交替二进制字符串的最少操作数【字符串,模拟】1353
- 51单片机项目(24)——基于51单片机的温控风扇protues仿真
- 从 MySQL 的事务 到 锁机制 再到 MVCC
- PHP代码审计之基础 方法 思路 流程
- 聚醚胺市场分析:预计到2025年将达到10亿美元
- ResNet论文阅读和简单实现
- [NSSRound#3 Team]This1sMysql
- Flink Has Become the De-facto Standard of Streaming Compute