【每日一题】被列覆盖的最多行数

Tag

【二进制枚举】【矩阵】【2024-01-04】

---

题目来源

2397. 被列覆盖的最多行数

---

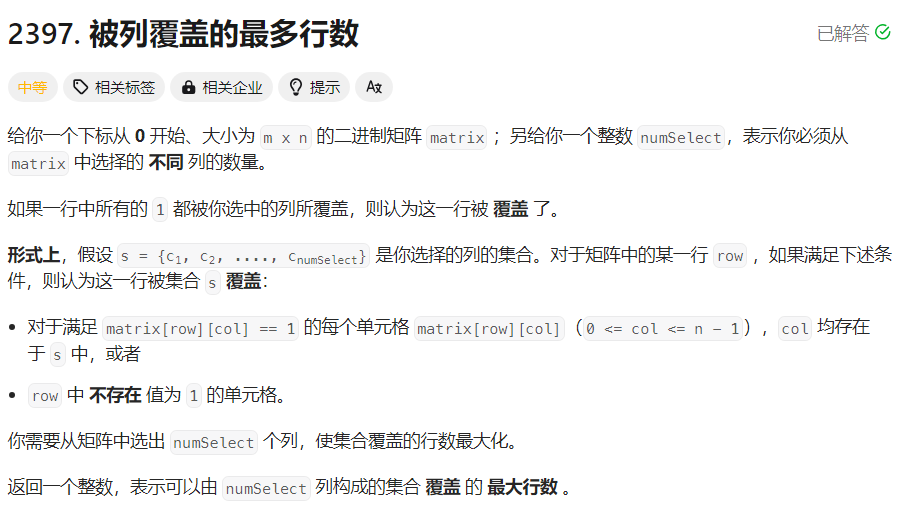
解题思路

方法一：二进制枚举

思路

使用二进制枚举所有选中列的集合，对于集合中的每一个二进制数，从低位到高位，第 i 位为 1 则表示第 i 列被选择，否则表示第 i 列没有被选择。

同时使用一个二进制数组 mask 来记录矩阵每一行的 0 1 元素。

接着遍历每一个选择了 numSelect 个列的子集，在每一个子集下计算矩阵的所有行中 符合条件 的最大列数。符合条件指的是矩阵的当前行中元素值为 1 对应的列一定要被选，即满足 (subSet & row) == row，row 表示矩阵当前行元素的二进制表示，subSet 表示选择了 numSelect 个列的子集。

算法

class Solution {
public:
    int maximumRows(vector<vector<int>>& matrix, int numSelect) {
        int m = matrix.size(), n = matrix[0].size();
        vector<int> mask(m);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                mask[i] |= matrix[i][j] << j;
            }
        }

        int res = 0;
        for (int subSet = 0; subSet < (1 << n); ++subSet) { // 遍历所有子集
            if (__builtin_popcount(subSet) == numSelect) {  // 选择了 numSelect 列的子集
                int rowCovered = 0;
                for (int row : mask) {                      // 遍历矩阵的所有行
                    if ((row & subSet) == row) {            // 矩阵所有元素值为 1 的列一定要被选
                        ++rowCovered;
                    }
                }
                res = max(res, rowCovered);
            }
        }
        return res;
    }
};

复杂度分析

时间复杂度：$O(m\times 2^n)$，$m$ 和 $n$ 分别为矩阵的行数和列数。

空间复杂度：$O(m)$。

---

写在最后

如果您发现文章有任何错误或者对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度的方法，欢迎评论区交流。

最后，感谢您的阅读，如果有所收获的话可以给我点一个 👍 哦。