逻辑回归（Logistic Regression）

回顾

Linear Regression

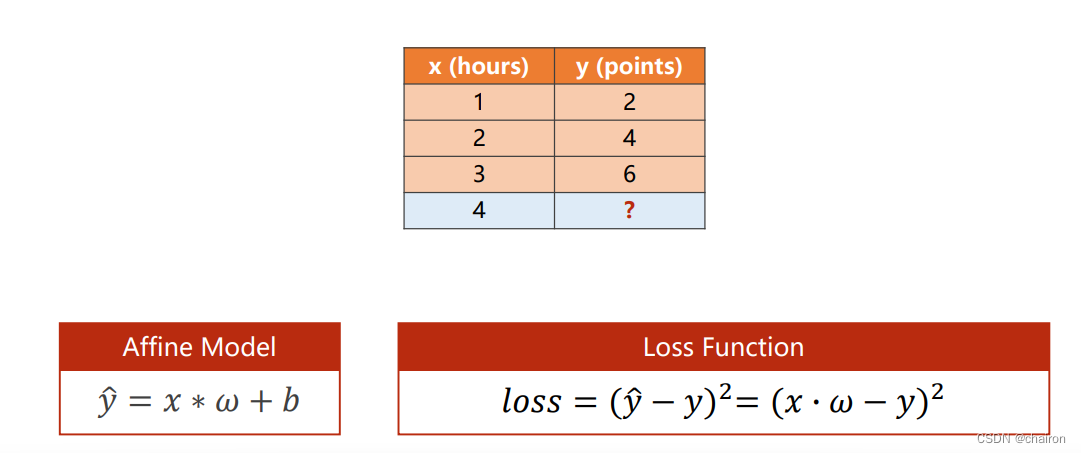
线性回归是用于预测连续值，做预测；而逻辑回归是预测离散值，即是用来分类的。

分类任务

The MNIST Dataset

手写数字数据集，包含训练集：60000样本；测试集：10000样本，共10类别

torchvision库里面包含有一些常用的数据集。

import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=True, download=True)#root:数据集下载路径；train=True：训练集
test_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=False, download=True)

The CIFAR-10 dataset

• Training set: 50,000 examples,
• Test set: 10,000 examples.
• Classes: 10

train_set = torchvision.datasets.CIFAR10(root='../dataset/mnist', train=True, download=True)
test_set = torchvision.datasets.CIFAR10(root='../dataset/mnist', train=False, download=True)

回归VS分类

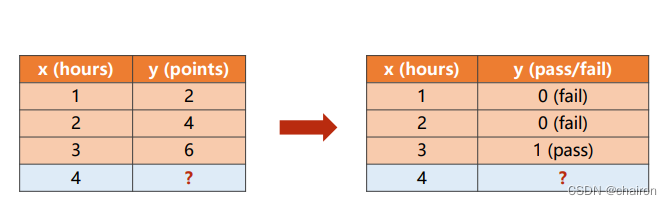
在之前的回归任务中，我们是预测分值是多少，在分类任务中就可以变成根据学习时间判断是否能通过考试，即考研分为两类：fail、pass。我们的任务就是计算不同学习时间x分别是fail、pass的概率。（二分类问题其实只需要计算一个概率；另一个概况就是1-算的概率）
如果预测pass概率为0.6，fail概率就是0.4，那么判断为pass。

在分类问题中，模型输出的就是输入属于哪一个类别的概率！
概率取值[0,1],预测值y_hat不一定在这个取值区间。因此我们需要把得到的预测值y_hat通过激活函数隐射为[0,1]区间。

sigmoid函数

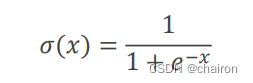
sigmoid函数在x无限趋近于正无穷、负无穷时，y无线趋近于1、0；可以看到当x非常大或者非常小的时候，函数梯度变化就非常小了。这种函数称为饱和函数。

逻辑回归

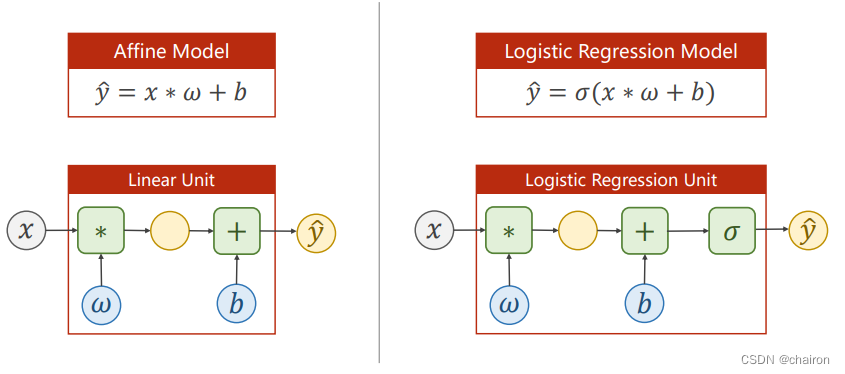
逻辑回归模型

只是在线性回归之后加了一个sigmoid激活函数！将值映射在【0，1】之间。

损失函数

MSE loss：计算数值之间的差异
BCE loss：计算分布之间的差异

分析：如果y=1，1-y=0,loss=-log y_hat,需要loss尽可能小，那么y_hat就要尽可能大，即尽可能接近1.
如果y=0，1-y=1，loss=-log(1-y_hat）,需要loss尽可能小，那么y_hat值越接近0越好。（log 1=0）
对数函数图：

Mini-Batch loss：BCE loss 求均值

实现

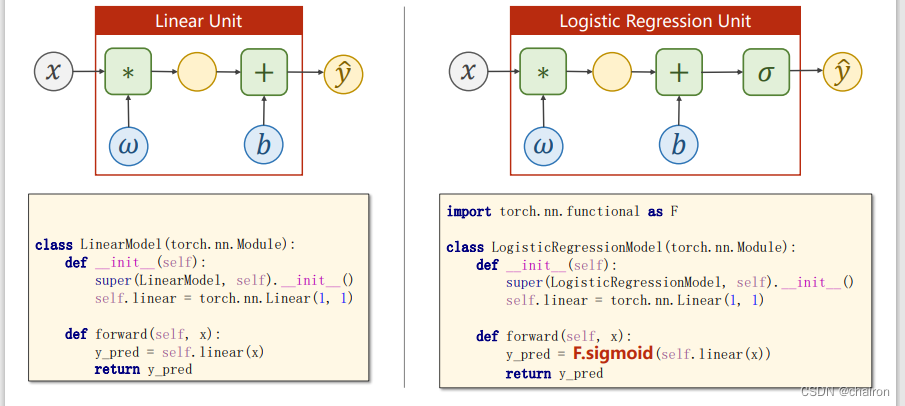
代码

逻辑回归实现同样是四个步骤：

1. 准备数据集
2. 设计模型
3. 定义损失函数和优化器
4. 模型训练

请先自己尝试根据上述步骤完成逻辑回归代码的实现，并且绘出学习时间hour与pass的可能性之间的关系。

# import torchvision
# train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=True, download=True)#root:数据集下载路径；train=True：训练集
# test_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=False, download=True)


# train_set = torchvision.datasets.CIFAR10(root='../dataset/mnist', train=True, download=True)
# test_set = torchvision.datasets.CIFAR10(root='../dataset/mnist', train=False, download=True)
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt

# 1.Prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
#-------------------------------------------------------#
# 2.Design model using Class
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)
    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x))#多了一个sigmid函数
        return y_pred

model = LogisticRegressionModel()

# 3.Construct loss and optimizer
#-------------------------------------------------------#
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#-------------------------------------------------------#

# 4.Training cycle
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

# test and plot
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))#将转换为tensor，变成200行，1列
y_t = model(x_t)
y = y_t.data.numpy()#tensor转化为numpy形式
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')#在概率=0.5时画一条红色直线
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()