【三自由度机械臂运动学正逆解实现细节】

前言

使用craig版本的DH建模，即一般认为的M-DH。

坐标系

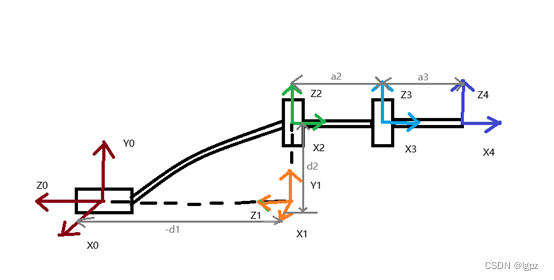
1.首先沿着转轴确定Z轴位置，方向自定。
2.找到与相邻两Z轴均相交的公法线（注意不能是公法面上的任意一条公法线，根据DH准则必须与两Z轴相交），Xi-1沿着Zi-1与Zi的公法线，方向自定。
3.由右手法则确定Y轴。
4.基坐标系尽量与坐标系1重合。
5.最后一个坐标系尽量与前一个重合。

DH参数

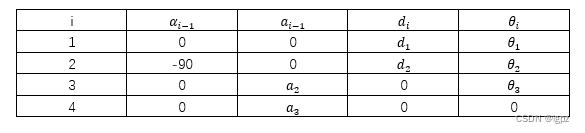
1.αi-1是Zi-1绕Xi-1旋转到Zi的角度，从Xi-1看逆时针为正。
2.ai-1是Zi-1沿着Xi-1到Zi的距离。
3.di是Xi-1沿着Zi到Xi的距离，可以看到X0是沿着Z1的反方向移动d1才与X1重合的，所以我在图中给d1前加了个负号。
4.θi即Zi的转角，也就是从Zi上看Xi与Xi-1间的夹角。

齐次变换矩阵

按照M-DH建立的DH参数都可以直接带入上面的变换矩阵中。
这里比较麻烦的是带未知数的矩阵运算，我找到这篇用python辅助计算的博客可以很好的解决：
https://blog.csdn.net/uuuuur/article/details/106608335
最后也是得到了正向运动学变换矩阵

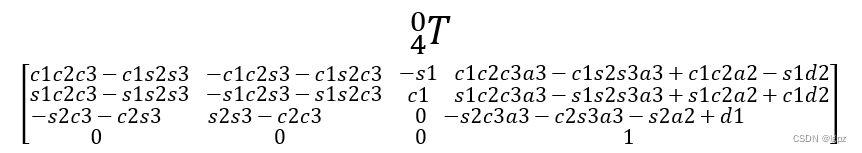
逆解

这里用符号Ai代替Ti，假设给出的位姿为T

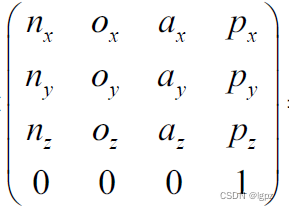
做一步变换

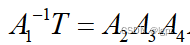
可以得到较为简洁的等式关系，更复杂的情况不能完全求出角度就继续左乘A2…
这里就不手打我的结果了
主要提一下这里比较重要的数学工具
1.θ = atan2(y,x) = atan2(sinθ，cosθ)
这个函数可以根据xy的正负确定所在象限，求出-pi到pi的角度，这在角度求解中很有用所以我的逆解最后都化成这个函数表示，尽管我有时已经知道了sinθ或cosθ。
2.
把等式化为Asin φ+Bcos φ+C=0的形式
可以直接得到

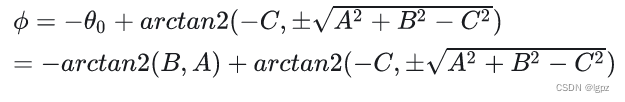
推导见https://zhuanlan.zhihu.com/p/338572834

验证逆解算法

这里采用输入十组原始点位然后通过逆解求出角度再通过变换矩阵计算出新的点位，对比点位是否有偏差判断逆解算法正确性。

import numpy as np
import math
import matplotlib.pyplot as plt


# 定义逆解算法和转换矩阵
def inverse_kinematics(pos):
    # 逆解算法
    value = pos[0] ** 2 + pos[1] ** 2 - 4
    if value < 0:
        print("无法计算：pos[0] ** 2 + pos[1] ** 2 - 4的值小于0")
        return -1
    else:
        a = -math.atan2(pos[1], -pos[0]) + math.atan2(2, math.sqrt(value))
    k1 = -1 - pos[2]
    k2 = pos[0] * math.cos(a) + pos[1] * math.sin(a)
    K = (k1 ** 2 + k2 ** 2 - 5) / 4
    value = k1 ** 2 + k2 ** 2 - K ** 2
    if value < 0:
        print("无法计算：k1 ** 2 + k2 ** 2 - K ** 2的值小于0")
        return -1
    else:
        b = -math.atan2(k2, k1) + math.atan2(K, math.sqrt(value))
    c = math.atan2(k1 - 2 * math.sin(b), k2 - 2 * math.cos(b)) - b
    # 返回角度a, b, c
    return a, b, c


def transformation_matrix(a, b, c):
    # 转换矩阵
    px = (3 * math.cos(c) + 2) * math.cos(a) * math.cos(b) - 3 * math.cos(a) * math.sin(b) * math.sin(c) - 2 * math.sin(
        a)
    py = (3 * math.cos(c) + 2) * math.sin(a) * math.cos(b) - 3 * math.sin(a) * math.sin(b) * math.sin(c) + 2 * math.cos(
        a)
    pz = -1 - 3 * (math.sin(b) * math.cos(c) + math.cos(b) * math.sin(c)) - 2 * math.sin(b)
    # 返回转换矩阵
    return px, py, pz


def calculate_xyz(inverse_kinematics, transformation_matrix, pos):
    # 使用逆解算法计算角度
    a, b, c = inverse_kinematics(pos)

    # 使用转换矩阵计算新的xyz值
    new_pos = transformation_matrix(a, b, c)

    return new_pos


# 测试程序
# 假设有一系列的位置数据
positions = [
    np.array([1, 2, -3]),
    np.array([0, 2, -6]),
    np.array([5, 2, -1]),
    np.array([4, 2, -1]),
    np.array([5, 1, -1]),
    np.array([3, 2, -3]),
    np.array([2, 3, -1]),
    np.array([4, 0, -1]),
    np.array([3, 2, 1]),
    np.array([4, 1, 2]),
    # 更多数据...
]
# 用于存储新位置的列表
new_positions = []
# 遍历每组数据
for pos in positions:
    # 计算逆解算法的角度
    a, b, c = inverse_kinematics(pos)
    # 使用转换矩阵计算新的xyz值
    new_pos = transformation_matrix(a, b, c)
    # 对新位置进行格式化，保留两位小数
    new_pos = [round(num, 2) for num in new_pos]
    new_positions.append(new_pos)
    # 打印新的xyz值
    print('新的xyz值：', new_pos)
# 绘制原始位置和计算出的新位置
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 原始位置
for i, pos in enumerate(positions):
    if i == 0:
        ax.scatter(pos[0], pos[1], pos[2], c='b', label=f'original pos')
    ax.scatter(pos[0], pos[1], pos[2], c='b')
# 计算出的新位置
for i, new_pos in enumerate(new_positions):
    if i == 0:
        ax.scatter(new_pos[0], new_pos[1], new_pos[2], c='r', label=f'new pos')
    ax.scatter(new_pos[0], new_pos[1], new_pos[2], c='r')
# 设置坐标轴标签
ax.set_xlabel('X ')
ax.set_ylabel('Y ')
ax.set_zlabel('Z ')
# 显示图例
plt.legend()
# 显示图形
plt.show()

结果

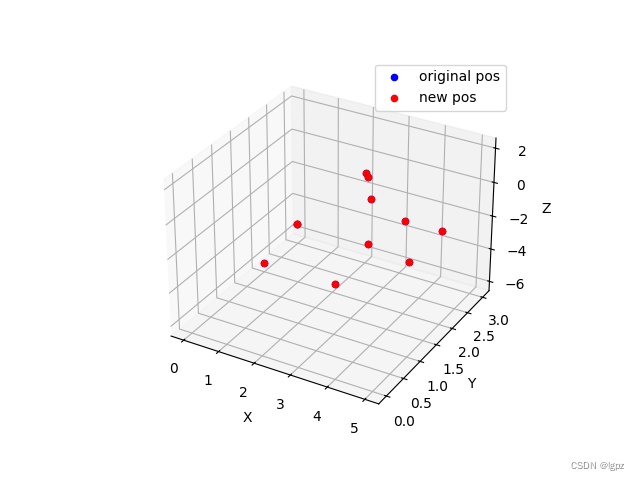
可以看到原始点位已经被新的点位完全覆盖了。

后记

目前只能指定位置，后续研究姿态的算法。

追更：

1.使用模运算将角度转换到-π到π的范围

import math

# 定义一个角度值（以弧度为单位）
angle = 3 * math.pi  # 这个角度大于π

# 使用模运算将角度转换到-π到π的范围
new_angle = (angle + math.pi) % (2 * math.pi) - math.pi

print(new_angle)  # 输出: -3.141592653589793