机器人中的数值优化之线性共轭梯度法

欢迎大家关注我的B站：

偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)

本文ppt来自深蓝学院《机器人中的数值优化》

目录

1.无约束优化方法对比

2.Hessian-vec product

3.线性共轭梯度方法的步长?编辑

4.共轭梯度方向的求解

5.线性共轭梯度方法整体流程

---

1.无约束优化方法对比

拟牛顿方法和牛顿共轭梯度方法是最优的，实现收敛速率与iteration work之间的平衡

2.Hessian-vec product

?hessian矩阵需要n方的复杂度，逆需要n三次方的复杂度，我们求解d需要hessian矩阵的逆

hessian与向量的乘积经过泰勒展开的简化可以变为只需求两次梯度

3.线性共轭梯度方法的步长

?A应该也是未知的，我们只能输入x得到Ax的值

?

?求解线性方程这个任务转化为求二次函数的最小值

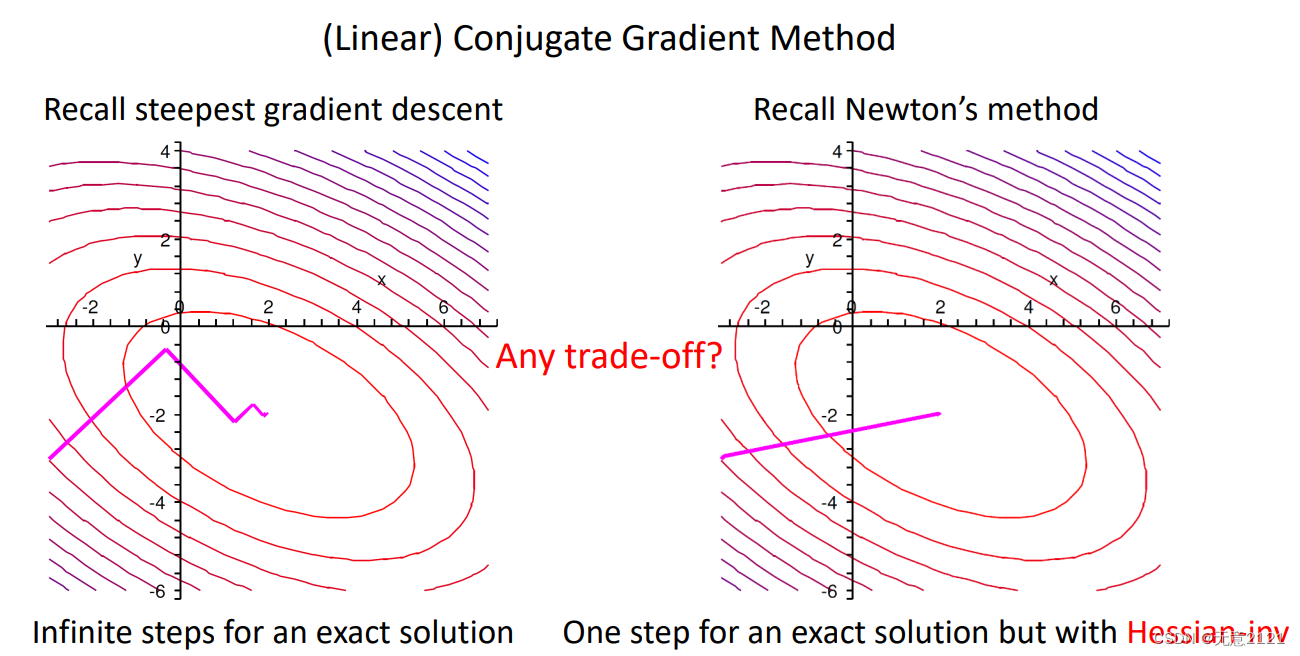
最速下降法收敛比较慢

牛顿方法需要涉及Hessian求逆

如果A=I，那么等高线是圆，n维则是对应超球，但是每次的迭代都是相互垂直的，只要n步这样正交的方向迭代搜索就能获得精确的最小值?

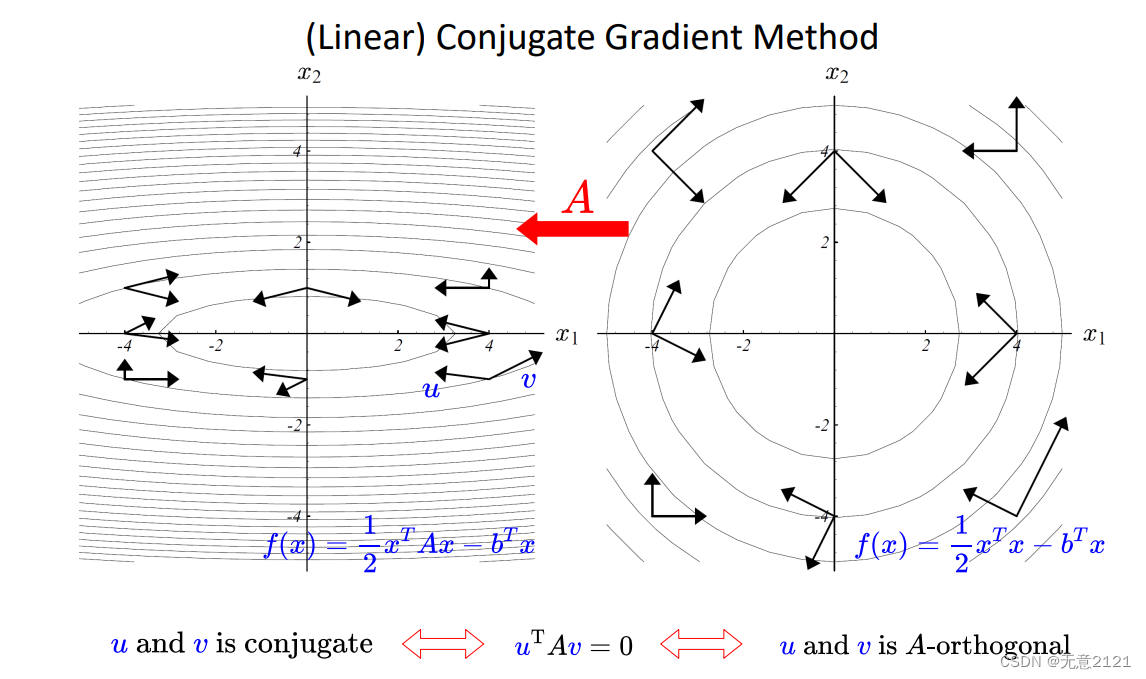
对于A！=I时，等高线为椭球，相当于做了仿射变换，原来的正交，现在则是共轭，定义如上

这里对步长进行求导则可以得到步长的闭式解，并且由其形式可看出我们只需要知道Ax这样输入x得出Ax的值的接口就行

4.共轭梯度方向的求解

施密特正交化就是不断把基底方向的分量减掉，剩下的就是和已经存在的基底正交的另一个基底?

共轭的施密特正交化与一般的施密特正交化的区别就是内积中间有系数矩阵A

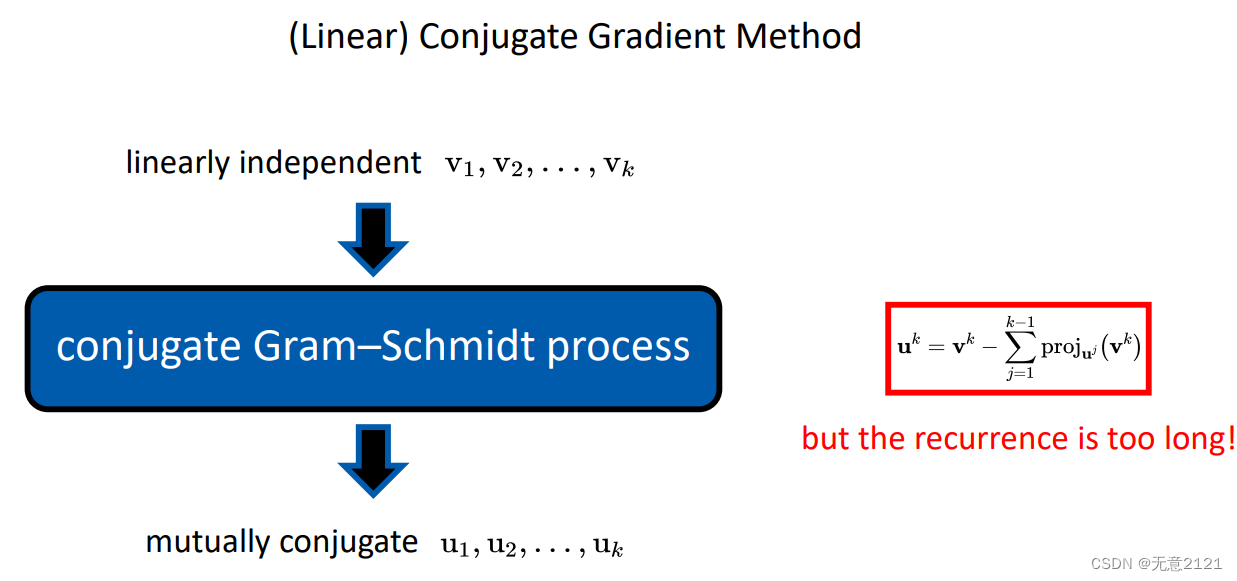
按部就班来还是k方的复杂度，实际上可以增量式地计算

这里令每一次Vk是残差，但这个残差已经把在之前的共轭投影上都是零了

5.线性共轭梯度方法整体流程