Java常用类---Math类和Random类

Math类

简介

Java中，Math类包含了用于执行基本数学运算的属性和方法。Math类的方法都被定义为static形式(静态方法)，通过Math类可以直接在主函数中直接调用。

如下图所示，Math.PI等于圆周率π、Math.E等于常量e……等属性和方法。

部分Math类方法介绍

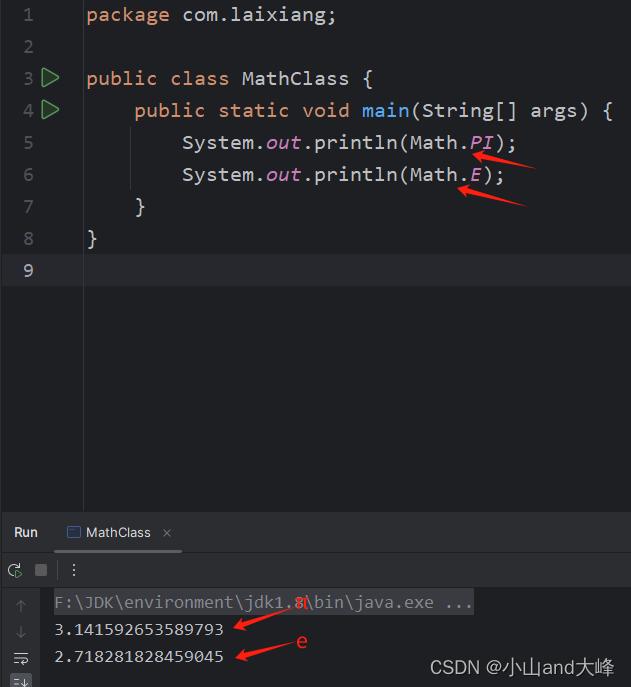
1. Math.abs 求绝对值，代码如下式所示。

   public static void main(String[] args) {
    ? ? ? ?int i = -1;
    ? ? ? ?double j = -1.5;
    ? ? ? ?//Math.abs方法输出绝对值(可为整数或小数)
    ? ? ? ?System.out.println(i+" 的绝对值结果为："+Math.abs(i));
    ? ? ? ?System.out.println("==============================");
    ? ? ? ?System.out.println(j+" 的绝对值结果为："+Math.abs(j));
    ?  }

   运行结果，如下图所示。

   

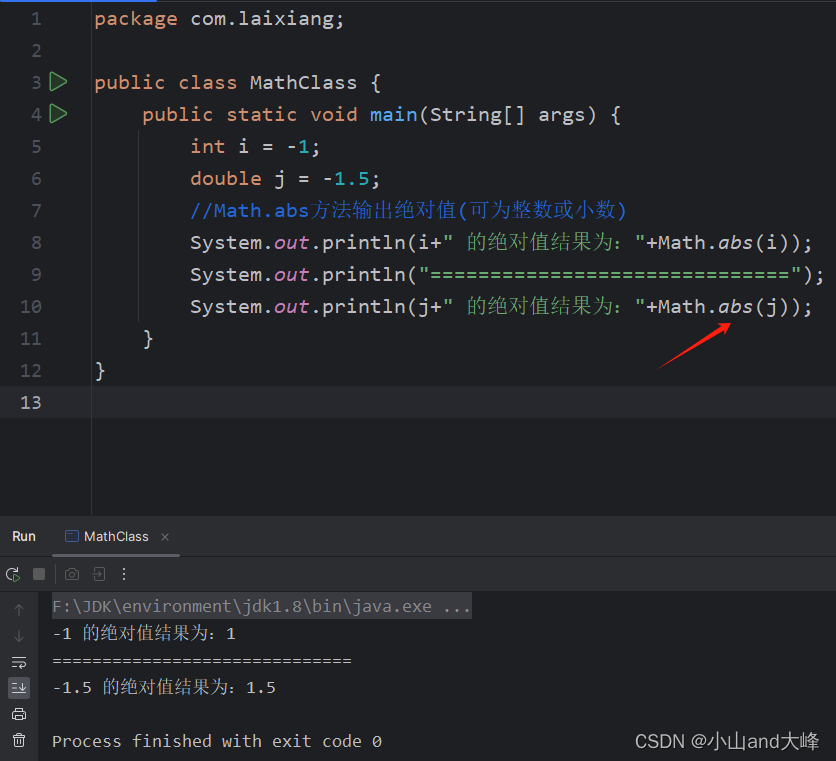
2. Math.sin 正弦函数，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?double i = 30;
    ? ? ? ?//将角度转换为弧度
    ? ? ? ?double j = Math.toRadians(i);//j == π/6
    ? ? ? ?System.out.printf("弧度值为："+"%.6f%n",j);
    ? ? ? ?System.out.printf("正弦值为："+"%.2f%n",Math.sin(j));
    ? ? ? ?//将弧度转换为角度
    ? ? ? ?double k = Math.toDegrees(j);//k == 30°
    ? ? ? ?System.out.printf("角度为："+"%.2f%n",k);
    ?  }

   其中：Math.toDegrees为弧度转化为角度，Math.toRadians为角度转化为弧度。

   运行结果，如下图所示。

   

   同理可得，余弦函数Math.cos、正切函数Math.tan、反正弦函数Math.asin、反余弦函数Math.acos、反正切函数Math.atan、商的反正切函数Math.atan2的使用与上述相当。

   注：使用Math.sin等方法时，传入参数是角度，角度单位是弧度值形式。

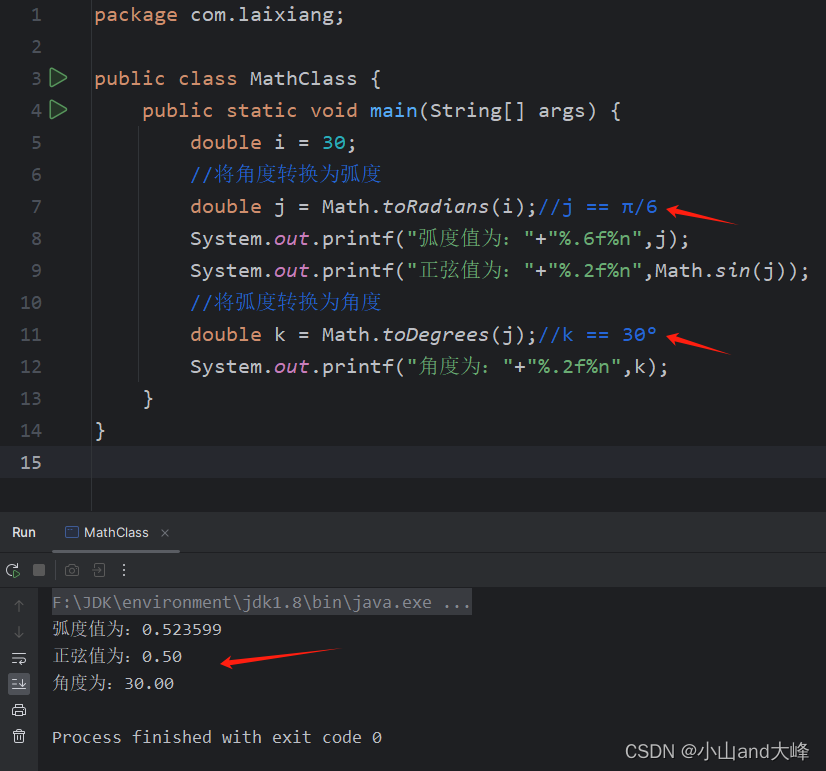
3. Math.ceil 对某数进行向上取整，ceil是天花板的意思，即返回大的值，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?double a = -10.2;
    ? ? ? ?double b = -0.2;
    ? ? ? ?double c = -1.7;
    ? ? ? ?double d = 2.5;
    ? ? ? ?/*对某数进行向上取整。
    ? ? ? ? *在本例中某数是指变量a、b、c、d
    ? ? ? ? */
    ? ? ? ?System.out.println(Math.ceil(a));
    ? ? ? ?System.out.println(Math.ceil(b));
    ? ? ? ?System.out.println(Math.ceil(c));
    ? ? ? ?System.out.println(Math.ceil(d));
    ?  }

   运行结果，如下图所示。

   

4. Math.floor 向下取整，floor是地板的意思，即返回小的值，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?double a = -10.2;
    ? ? ? ?double b = -0.2;
    ? ? ? ?double c = -1.7;
    ? ? ? ?double d = 2.5;
    ? ? ? ?/*对某数进行向下取整。
    ? ? ? ? *在本例中某数是指变量a、b、c、d
    ? ? ? ? */
    ? ? ? ?System.out.println(Math.floor(a));
    ? ? ? ?System.out.println(Math.floor(b));
    ? ? ? ?System.out.println(Math.floor(c));
    ? ? ? ?System.out.println(Math.floor(d));
    ?  }

   运行结果，如下图所示。

   

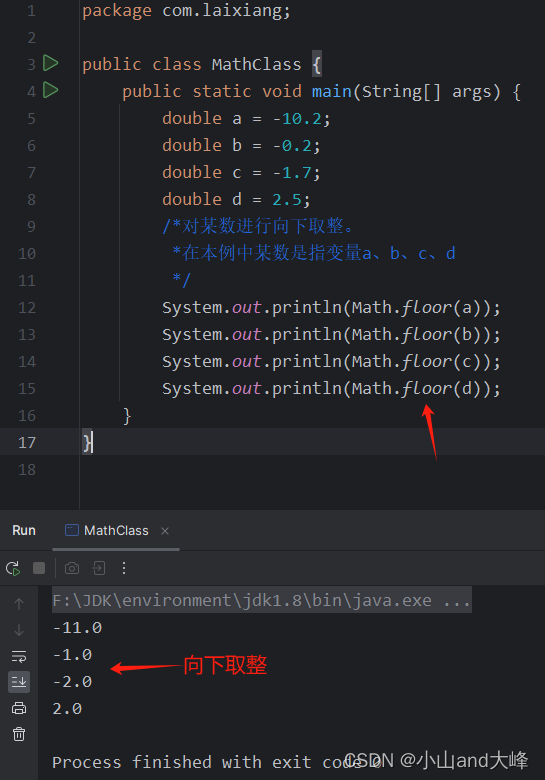
   注：与Math.ceil方法相同，Math.floor方法的返回值也是double形式。

5. Math.IEEEremainder(x, y) 求余数。其中，x为被除数，y为除数，返回值是根据IEEE 754标准返回余数，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?double x = 15;
    ? ? ? ?double y = 4;
    ? ? ? ?System.out.println("Math.IEEEremainder方法的余数结果为："+Math.IEEEremainder(x, y));
    ? ? ? ?System.out.println(x+"%"+y+"的余数结果为："+(x%y));
    ?  }

   运行结果，如下图所示。

   

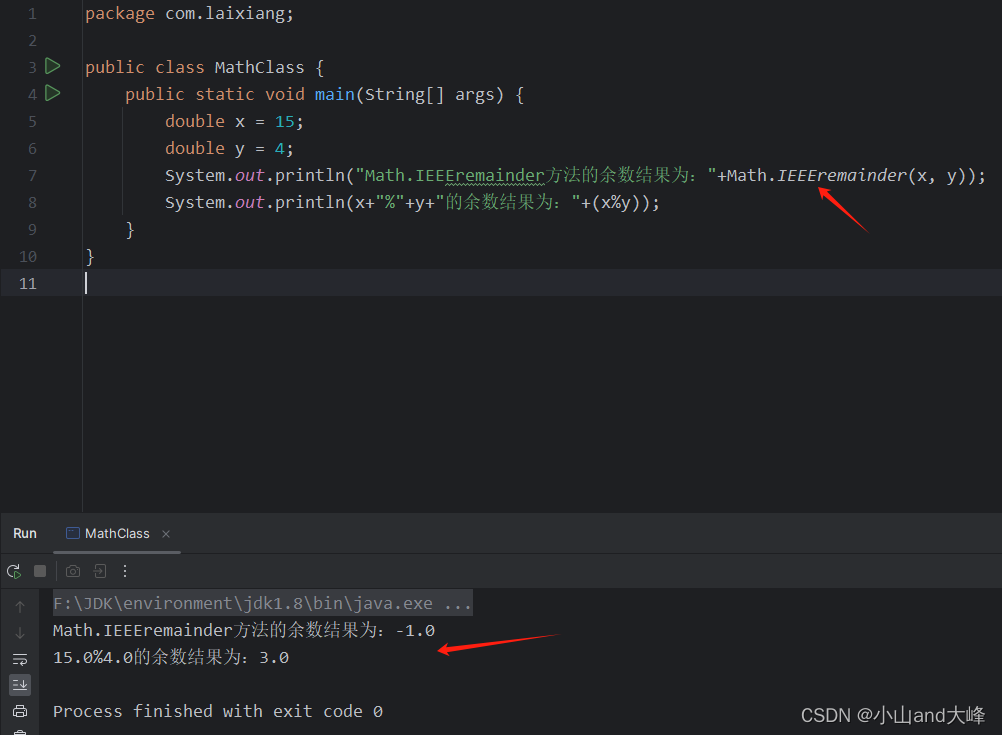
   补充：由上图可以看出，所得余数结果与15%(取余)4的结果有所不同。本质原因是n值的取值不同！！！

   Math.IEEEremainder和运算符"%"的返回的余数都等于x - y * n ，但前者的n是取最接近x/y的整数，如果x/y返回的是介于两个整数之间的数，则n取值为偶数的一方。eg：x = 15, y = 4, x/y在(3,4)两个整数区间内，故n取4。

   而对于运算符"%"来说，n取值为x/y的整数结果。eg：x = 15, y = 4, x/y的整数部分为3，故n取3。

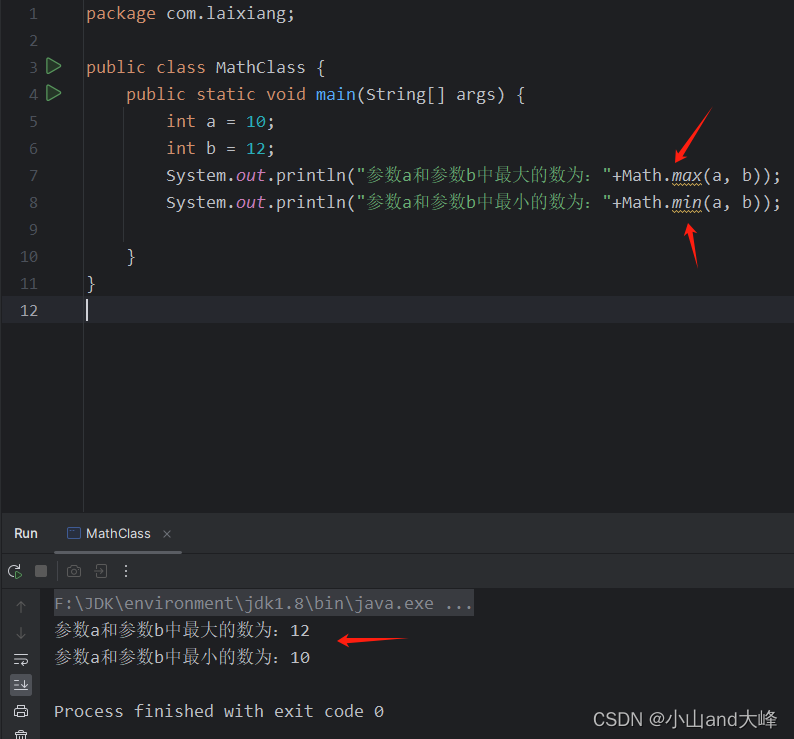
6. Math.max 比较并返回两数中的最大值，Math.min 比较并返回两数中的最小值，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?int a = 10;
    ? ? ? ?int b = 12;
    ? ? ? ?System.out.println("参数a和参数b中最大的数为："+Math.max(a, b));
    ? ? ? ?System.out.println("参数a和参数b中最小的数为："+Math.min(a, b));
   ?
    ?  }

   运行结果，如下图所示。

   

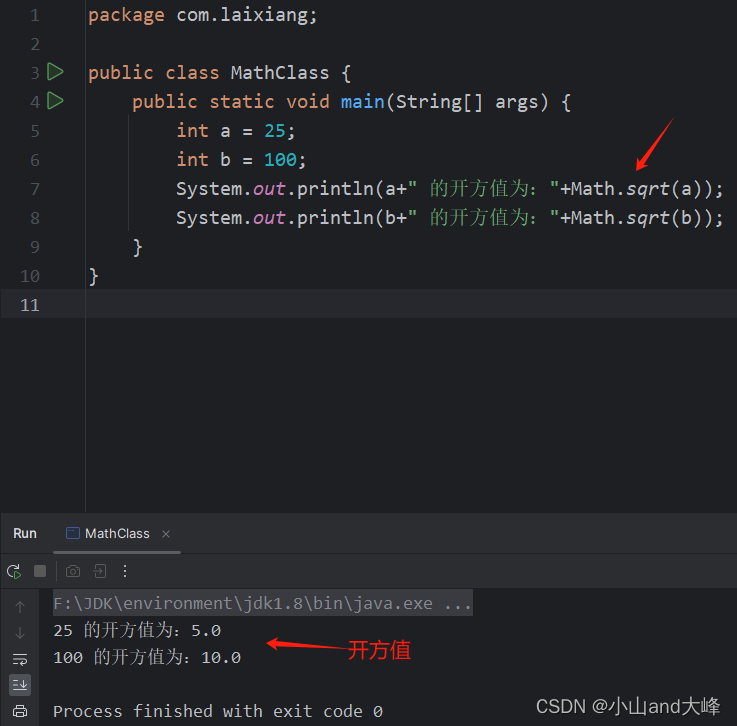
7. Math.sqrt 开平方，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?int a = 25;
    ? ? ? ?int b = 100;
    ? ? ? ?System.out.println(a+" 的开方值为："+Math.sqrt(a));
    ? ? ? ?System.out.println(b+" 的开方值为："+Math.sqrt(b));
    ?  }

   运行结果，如下图所示。

   

8. Math.pow 求某数的任意次方，代码如下式所示。

    ? ?public static void main(String[] args) {
    ? ? ? ?double x = 25;
    ? ? ? ?int y = 100;
    ? ? ? ?double a = 2;
    ? ? ? ?int b = 3;
    ? ? ? ?System.out.println(x+"的"+a+"次方为："+Math.pow(x, a));
    ? ? ? ?System.out.println(y+"的"+b+"次方为："+Math.pow(y, b));
    ?  }

   运行结果，如下图所示。

   

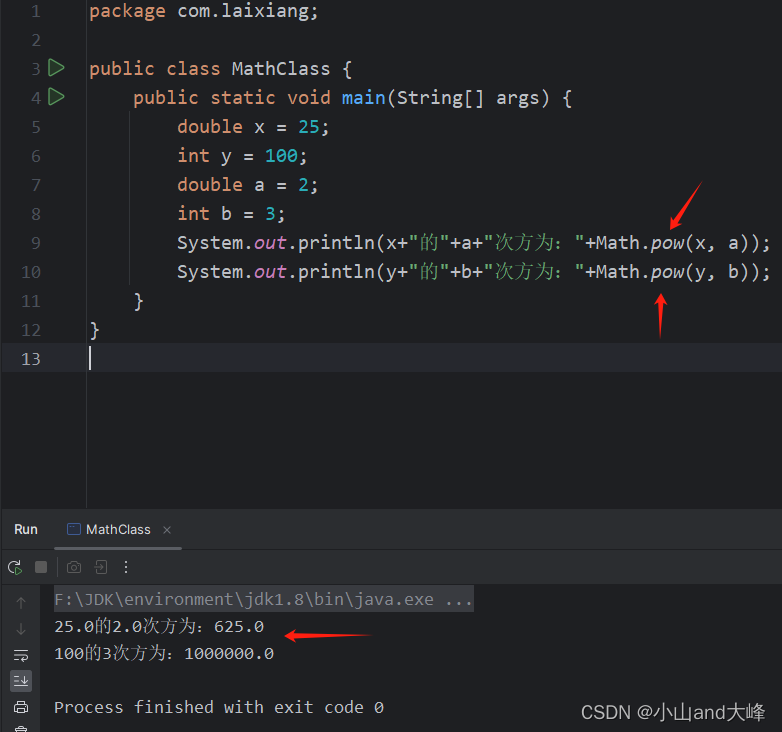
   其中，Math.pow(x, a)指的是求x的a次方，Math.pow(y, b)同理。当数值溢出的时候抛出ArithmeticException异常。

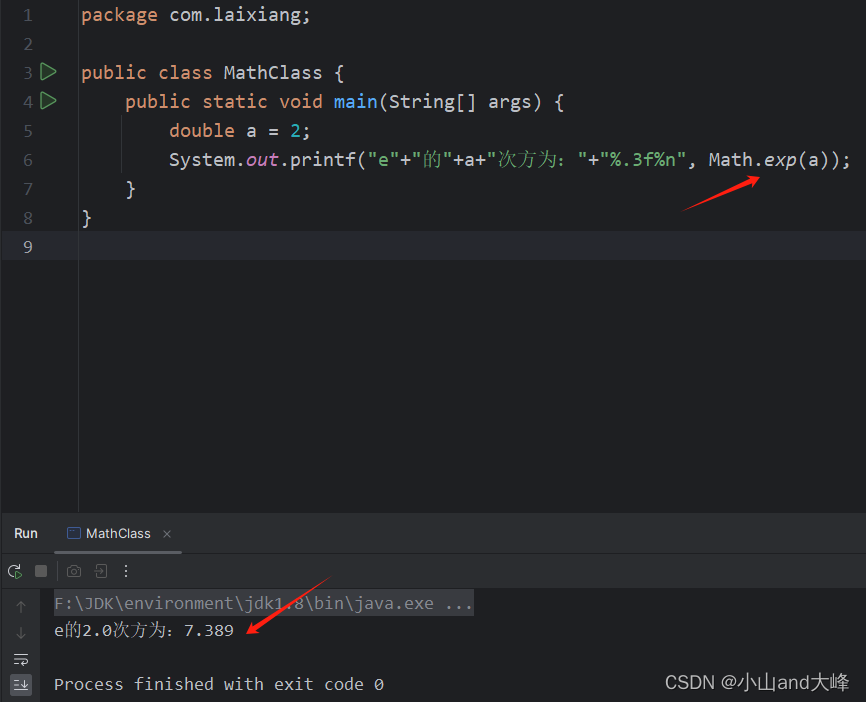
9. Math.exp 开平方，代码如下式所示。

       public static void main(String[] args) {
           double a = 2;
           System.out.printf("e"+"的"+a+"次方为："+"%.3f%n", Math.exp(a));
       }

   运行结果，如下图所示。

   

10. Math.log 自然对数，即以e为底的对数，代码如下式所示。

    public static void main(String[] args) {
        double a = 1000;
        double b = Math.pow(Math.E, 2);
        System.out.println("以10为底"+a+"的对数为："+Math.log10(a));
        System.out.printf("以e为底"+"e^2的对数为："+Math.log(b));
    }

运行结果，如下图所示。

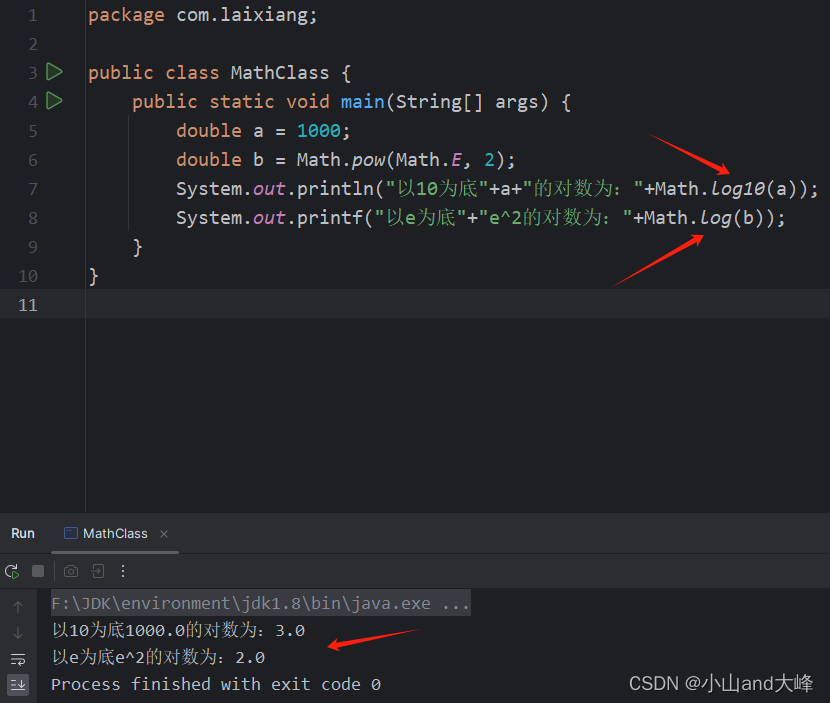
补充：Math.log10 指以10为底的对数，如上图所示。

1. Math.rint 四舍五入求距离x最近的整数，结果可能大于x，也可能小于x，代码如下式所示。

       public static void main(String[] args) {
           double x = -5.23;
           double x1 = 10.5;
           double x2 = 10.53;
           System.out.println(x +"经过Math.rint方法后，结果为："+Math.rint(x));
           System.out.println(x1 +"经过Math.rint方法后，结果为："+Math.rint(x1));
           System.out.println(x2 +"经过Math.rint方法后，结果为："+Math.rint(x2));
       }

   运行结果，如下图所示。

   

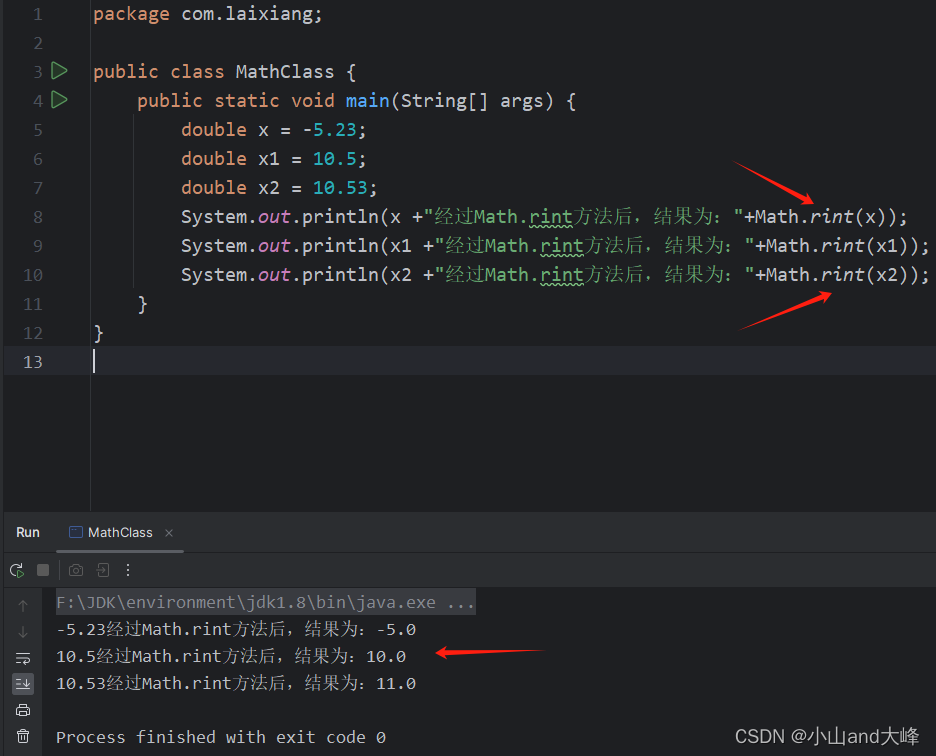
   其中，当取值为x.5时，rint方法计算距离最近的整数，返回偶数值，返回值的类型为double类型。

2. Math.round 四舍五入求距离x最近的整数，与Math.rint类似。但该方法返回值类型为int型或者long型，且对于x.5类型数据，不存在rint方法的问题，代码如下式所示。

       public static void main(String[] args) {
           double x = -5.23;
           double x1 = 10.5;
           double x2 = 10.53;
           float x3 = 12.5F;
           System.out.println(x +"经过Math.round方法后，结果为："+Math.round(x));
           System.out.println(x1 +"经过Math.round方法后，结果为："+Math.round(x1));
           System.out.println(x2 +"经过Math.round方法后，结果为："+Math.round(x2));
           System.out.println(x2 +"经过Math.round方法后，结果为："+Math.round(x3));
       }

   运行结果，如下图所示。

   

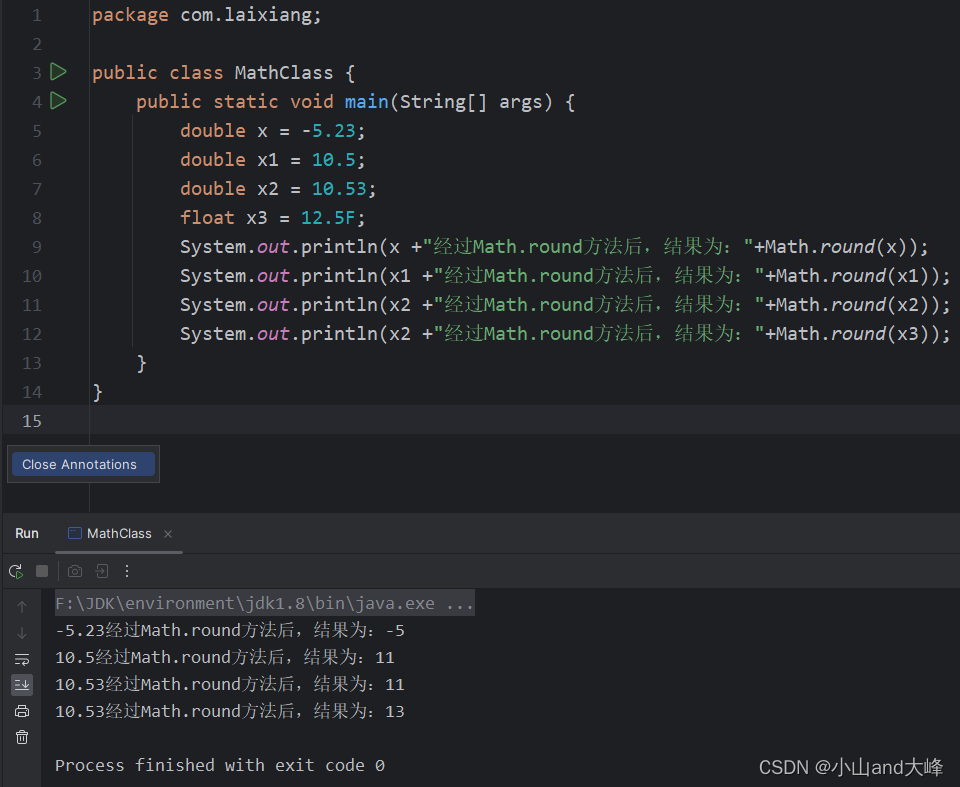
   注：Math.round方法中，当参数为float类型时，返回值为int类型。当参数为double类型时，返回值为long类型。

3. Math.random 返回0,1之间的一个随机数，范围在[0,1)，代码如下式所示。

       public static void main(String[] args) {
           System.out.println("输出一个在[0，1)之间的数："+Math.random());
           System.out.println("输出一个在[1，2)之间的数："+Math.random()+1);
       }

   运行结果，如下图所示。

   

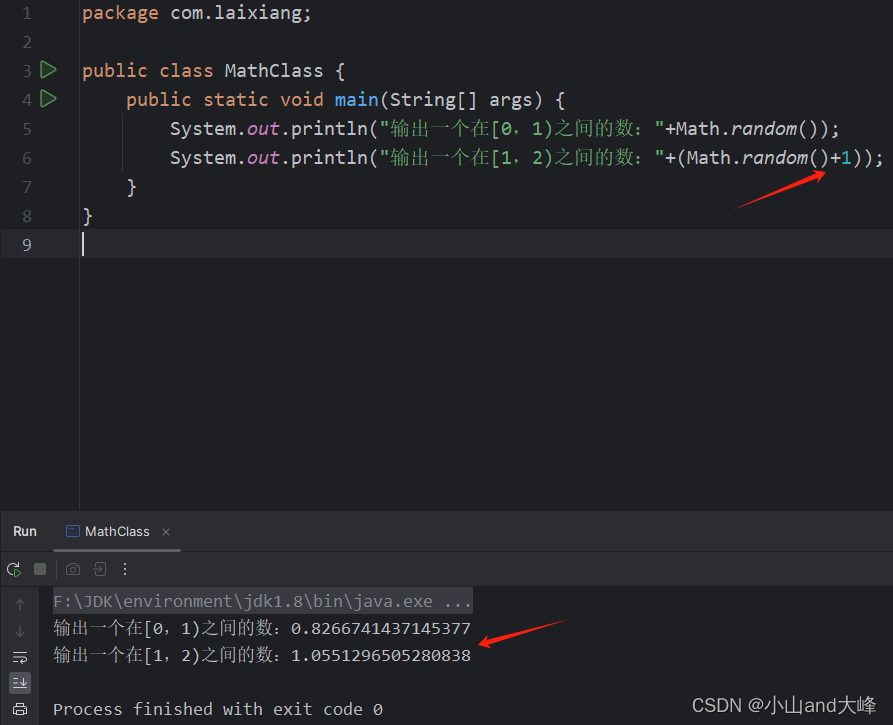
   补充：可以通过在Math.random()方法后加x来改变随机数产生的范围，新的范围为：[0+x, 1+x)

Random类

Random随机数生成方法

上一节，介绍了Math类中的random方法。调用这个方法能够返回一个范围在[0.0，1.0)之间的double值。

除此之外，在Random类中还存在另一种随机数生成方法。如下所示。

1. Random()：创建一个新的随机数生成器。

2. Random(long seed)：使用单个long种子创建一个新的随机数生成器。

   注：在创建一个Random对象的时候可以给定任意一个合法种子数，种子数只是随机算法的起源数字，和生成的随机数区间没有关系！！！

代码演示如下式所示。

    public static void main(String[] args) {
        //对象的种子缺省值为当前系统时间的毫秒数
        Random rand = new Random();
        //rand.nextInt()中的参数为随机数的上限，产生区间不包括上限。
        int i = rand.nextInt(200);
        System.out.println("产生的随机数为："+i);
    }

运行结果，如下图所示。

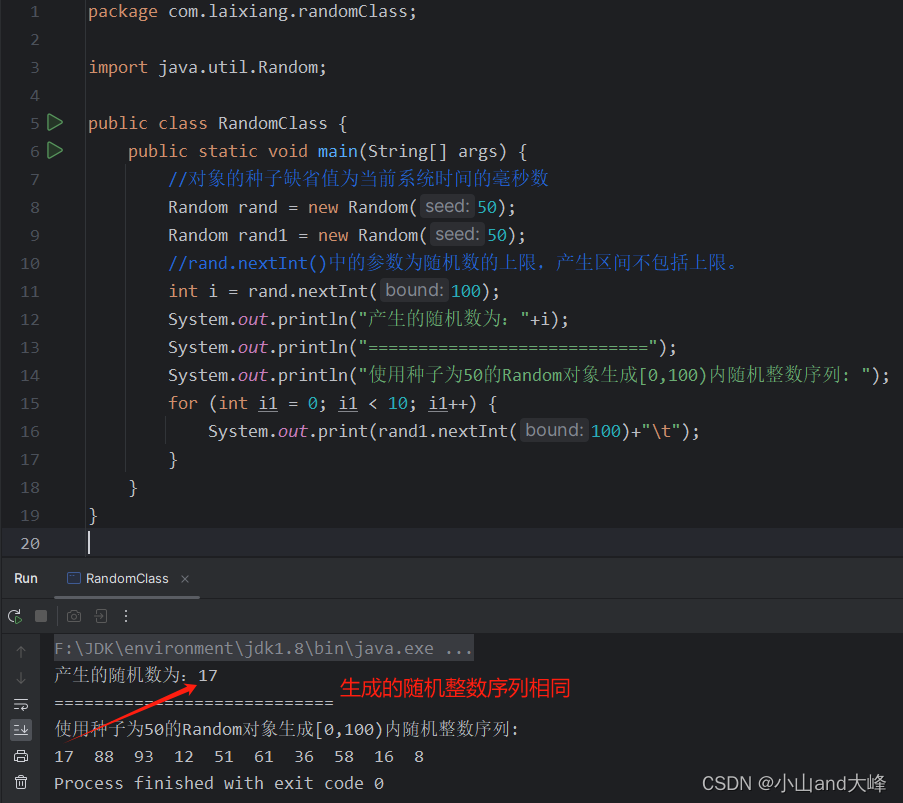
注：对于种子相同的Random对象，所生成的随机数序列一样！！！如下图所示。

Random类中部分方法介绍

1. nextBoolean() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、均匀分布的 boolean 值。

2. nextDouble() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、在0.0 和 1.0之间均匀分布的 double 值。

3. nextFloat() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、在0.0 和 1.0之间均匀分布的 float 值。

4. nextInt() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、均匀分布的 int 值。

5. nextLong() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、均匀分布的 long 值。

6. nextInt(int n) 返回一个伪随机数，它是从此随机数生成器的序列中取出的、在 0（包括）和指定值（不包括）之间均匀分布的 int 值。如下式所示。

   Random rand = new Random(50); 
   int i = rand.nextInt(100);//范围在[0, 100)
   System.out.println("产生的随机数为："+i);

7. nextGaussian() 返回下一个伪随机数，它是从此随机数生成器的序列中取出的、呈高斯（“正常地”）分布的 double 值，其平均值是 0.0，标准偏差是 1.0。

8. setSeed(long seed) 使用单个 long 种子设置此随机数生成器的种子。

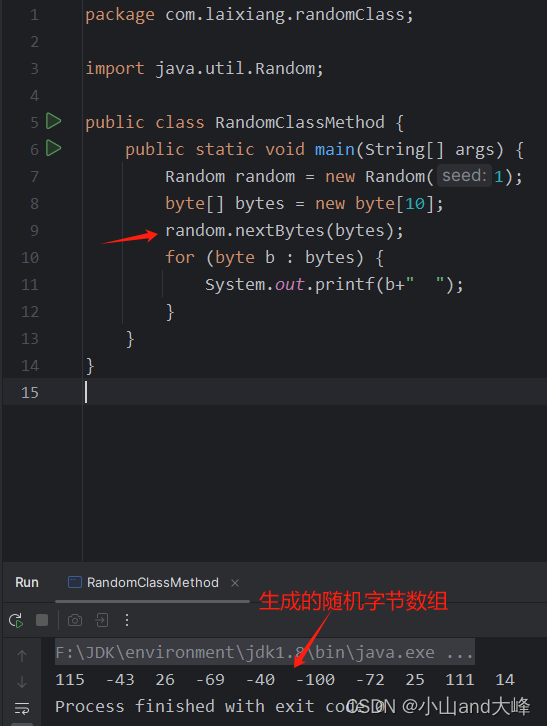
9. nextBytes(byte[] bytes) 生成随机字节并将其置于用户提供的字节数组中。如下图所示。

   

补充：生成[0.0, 1.0)之间的小数、生成[0.0, 5.0)之间的小数、生成[1.0, 2.5)之间的小数，如下图所示。

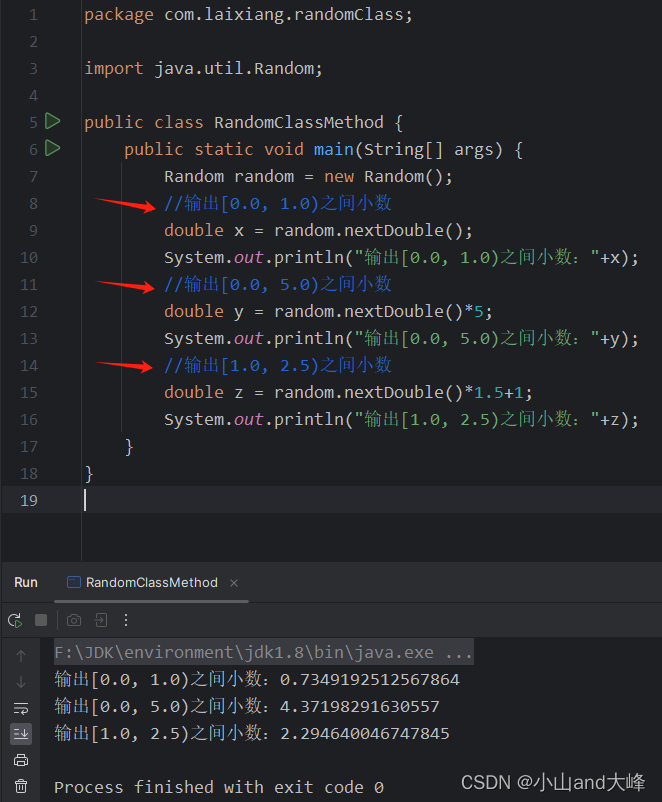
注：本质上是对区间的乘加。eg：[1.0, 2.5) == [(0.0* 1.5)+1 , (1* 1.5)+1)