C++算法学习五.栈与队列
根据代码随想录,记录学习一些算法经验?
1.栈与队列的理论基础
队列是先进先出,栈是先进后出。栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)。
STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。
队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器,?SGI STL中队列一样是以deque为缺省情况下的底部结构。
所以STL 队列也不被归类为容器,而被归类为container adapter( 容器适配器)。
2.用栈实现队列(232题)
题目描述:
使用栈实现队列的下列操作:
push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。
模拟题:使用两个栈来模拟即可实现,一个栈是输入栈,另一个是输出栈,注意弹出队列元素时候,要注意首先看输出栈是否为空,在看输入栈是否为非空,不为空全部压入栈中在弹出。
class MyQueue {
public:
stack<int>stIn;//输入栈
stack<int>stOut;//输出栈
MyQueue() {
}
void push(int x) {//压入队列,其实就是输入栈进栈
stIn.push(x);
}
int pop() {//弹出队列
if(stOut.empty()){//输出栈为空
while(!stIn.empty()){//输入栈不为空
stOut.push(stIn.top());//把全部输入栈压入到输出栈中
stIn.pop();//弹出输出栈的元素
}
}
int result = stOut.top();//结果就是输出栈弹出的元素
stOut.pop();//弹出元素
return result;
}
int peek() {//队头元素
int res = this->pop();//复用了Pop函数
stOut.push(res);
return res;
}
bool empty() {//判断是否为空,两个栈都空即为空
return stIn.empty() && stOut.empty();
}
};- 时间复杂度: push和empty为O(1), pop和peek为O(n)
- 空间复杂度: O(n)
3.用队列实现栈(225题)
题目描述:
使用队列实现栈的下列操作:
- push(x) -- 元素 x 入栈
- pop() -- 移除栈顶元素
- top() -- 获取栈顶元素
- empty() -- 返回栈是否为空
使用两个队列做法:一个队列实际操作,另一个队列进行辅助,下面实现代码:
class MyStack {
public:
queue<int>que1;//两个队列实现,队列2实现辅助 功能
queue<int>que2;//
MyStack() {
}
void push(int x) {
que1.push(x);//队列的压入就是相当于压栈
}
int pop() {//弹出元素
int size = que1.size();//计算队列的大小
size--;//先做一个减一操作留一个元素
while(size--){//将队列1转队列2中,队列1的头的元素压入队列2,再弹出
que2.push(que1.front());
que1.pop();
}
int result = que1.front();//队列1剩下的元素就是要弹出的元素
que1.pop();//弹出
que1 = que2;//队列2赋值给队列1
while(!que2.empty()){//清空队列2
que2.pop();
}
return result;//返回值
}
int top() {//队列尾就是栈头元素
return que1.back();
}
bool empty() {//队列1空了栈空
return que1.empty();
}
};队列2也就是在弹出元素作为辅助作用,
- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
下面用一个队列实现的:一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。
class MyStack {
public:
queue<int>que1;//1个队列实现
MyStack() {
}
void push(int x) {
que1.push(x);//队列的压入就是相当于压栈
}
int pop() {//弹出元素
int size = que1.size();//计算队列的大小
size--;//先做一个减一操作留一个元素
while(size--){//将队列1的头的元素压入队列1尾,再弹出
que1.push(que1.front());
que1.pop();
}
int result = que1.front();//队列1剩下的元素就是要弹出的元素
que1.pop();//弹出
return result;//返回值
}
int top() {//队列尾就是栈头元素
return que1.back();
}
bool empty() {//队列1空了栈空
return que1.empty();
}
};- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
4.有效的括号?(20题)
题目描述:给定一个只包括 '(',')','{','}','[',']'?的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 注意空字符串可被认为是有效字符串。
示例 1:
- 输入: "()"
- 输出: true
?使用栈来解法:括号匹配是典型栈解法应用,栈一般用来做对称匹配题目,需要注意字符串不匹配的情况,三种情况:左括号多余,括号不匹配,右括号多余,技巧:匹配左括号,右括号进栈,最后对比是否相等就可以,遇左进栈,遇右弹出比较。
class Solution {
public:
bool isValid(string s) {
stack<int>st;//申请一个栈
for(int i = 0;i < s.size(); i++){//遍历整个字符串
if(s[i] == '('){//遇到左括号全部把右括号压入栈
st.push(')');
}else if(s[i] == '{'){
st.push('}');
}else if(s[i] == '['){
st.push(']');
}else if(st.empty() || s[i] != st.top()){//判断右括号多余和括号不匹配的情况
return false;
}else{//相等弹出括号
st.pop();
}
}
return st.empty();//如果全部匹配,返回正确,否则是左括号多余情况,返回错误
}
};- 时间复杂度: O(n)
- 空间复杂度: O(n)
5.删除字符串中的所有相邻重复项?(1047题)
题目描述:给出由小写字母组成的字符串?S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
- 输入:"abbaca"
- 输出:"ca"
- 解释:例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
思路:删除相邻重复项,其实就是删除对称项的问题,首先需要考虑栈能否解决,这道题首先考虑好栈如何解决的,在定义一个字符串去接收,然后要注意字符串的顺序问题,栈存放遍历过的元素,
class Solution {
public:
void reverse(string& s,int start, int end){//自己定义的反转函数
for(int i = start,j = end;i < j;i++,j--){
swap(s[i],s[j]);
}
}
string removeDuplicates(string s) {//删除字符串所有相邻重复项
stack<int>st;//定义一个栈,一般来做对称匹配问题很好用
for(char c : s){//遍历每个字符串的字符
if(st.empty() || c != st.top()){//如果为空或者下一个字符不等于栈顶元素压入栈中
st.push(c);
}else{//就是栈顶元素相等就是遇到重复元素,已经消除了一对对称的元素
st.pop();
}
}
string t = "";//定义一个字符串去接收
while(!st.empty()){//将栈里的元素加入到字符串里
t += st.top();
st.pop();
}
reverse(t,0,t.size()-1);//因为加入字符串的顺序不对需要反转一次
return t;
}
};递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,
- 时间复杂度: O(n)
- 空间复杂度: O(n)
6.逆波兰表达式求值(150题)
题目描述:
根据 逆波兰表示法,求表达式的值。
有效的运算符包括?+ ,? - ,? * ,? /?。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例?1:
- 输入: ["2", "1", "+", "3", " * "]
- 输出: 9
- 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
其实相当于二叉树的后序遍历,运算符是中间节点,就是二叉树的后序遍历,这种运算有相邻字符串消除模式,想到栈的解法,
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st; //定义一个栈
for (int i = 0; i < tokens.size(); i++) {//从字符串遍历
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {//遇到了运算符进行运算
int num1 = st.top();//定义一个数去接收
st.pop();//然后从栈弹出
int num2 = st.top();//定义另一个数接收
st.pop();//弹出
if (tokens[i] == "+") st.push(num2 + num1);//判断哪种运算符,对其进行操作之后压入栈中
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {//不是运算符
st.push(stoi(tokens[i]));//stoi函数将字符串转换成整形,压入栈中
}
}
int result = st.top();//结果就是最后栈顶元素
st.pop(); //弹出
return result;
}
};- 时间复杂度: O(n)
- 空间复杂度: O(n)
7.滑动窗口最大值?(239题)
题目描述:
给定一个数组 nums,有一个大小为?k?的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k?个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
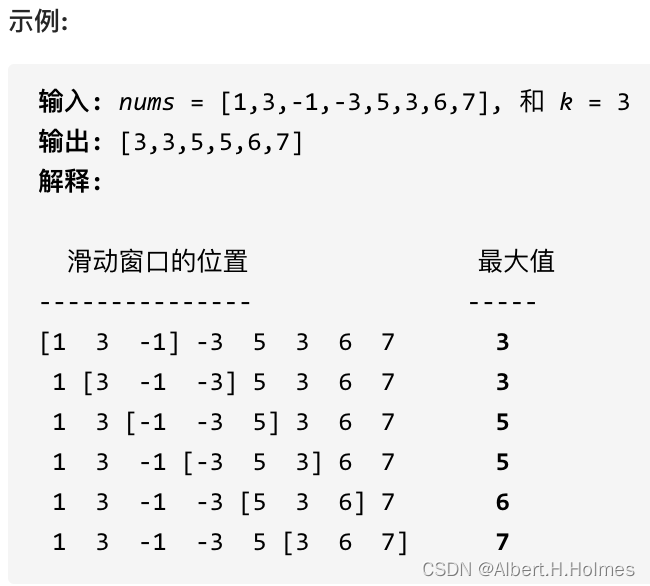
思路:首先优先级队列为何不行,因为如果排序了打乱了原来顺序,错误,所以我们采用自定义的单调队列来实现,要一个压入函数,和一个弹出函数,且告知队头元素就是我们需要的最大值我们的诉求,弹出元素:如果窗口移除元素等于单调队列出口元素,弹出元素,否则不操作,Push函数,如果元素大于入口元素,则将队列入口元素弹出,改变的其实是前面的值,不改变后面的局部最大保存下来,后面就是遍历操作即可。?
class Solution {
private:
class MyQueue{//自己实现的单调队列,其实就是维护一个所需的最大值而已
public:
deque<int>que;//使用deque实现单调队列,双端队列
void pop(int value){//实现一个自己定义的弹出函数,
if(!que.empty() && value == que.front()){//不能对空队列操作,如果要弹出的元素和队元素相等则弹出
que.pop_front();//这部分要注意从队头移除元素
}
}
void push(int value){//压入队列操作
while(!que.empty() && value > que.back()){//不能空队列操作,我们只需要维护最大值即可,所以从队尾弹出知道小于队尾元素
que.pop_back();
}
que.push_back(value);//如果小于就从队尾加入队列
}
int front(){//返回窗口的最大值也就是队头元素
return que.front();
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {//实现的函数
MyQueue que;
vector<int>result;//结果集
for(int i=0;i < k;i++){//现将前k 个元素加入队列
que.push(nums[i]);
}
result.push_back(que.front());//得到一个结果
for(int i = k;i<nums.size();i++){//再将后面元素操作
que.pop(nums[i - k]);//移除最前面的元素
que.push(nums[i]);//压入最后的元素
result.push_back(que.front());//记录对应最大值
}
return result;
}
};- 时间复杂度: O(n)
- 空间复杂度: O(k)
8.前 K 个高频元素(347题)?
题目描述:
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
- 输入: nums = [1,1,1,2,2,3], k = 2
- 输出: [1,2]
思路: 统计元素出现频率,对频率排序,找出前k个频率的元素,
使用数据结构map,排序使用优先级队列,
priority_queue利用max-heap(大顶堆)完成对元素的排序,这个大顶堆是以vector为表现形式的complete binary tree(完全二叉树)。
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子的值。?如果父亲结点是大于等于左右孩子就是大顶堆,小于等于左右孩子就是小顶堆。大顶堆(堆头是最大元素),小顶堆(堆头是最小元素)。
如果使用大根堆返回最小前K个元素
我们要用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
class Solution {
public:
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {//自定义一个比较规则我们要传入的哈希值形式
return lhs.second > rhs.second;//比较的是第二个也就是数的个数
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {//实现的函数
unordered_map<int, int> map;//定义一个哈希表map
for (int i = 0; i < nums.size(); i++) {//对数组的每个元素进行记录个数
map[nums[i]]++;
}
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison>
pri_que;//定义一个优先级队列小根堆排序方式
//将哈希表遍历
for (unordered_map<int, int>::iterator it = map.begin();
it != map.end(); it++) {
pri_que.push(*it);//将哈希值插入压入队列
//固定大小为k,超过了弹出小元素
if (pri_que.size() > k) {
pri_que.pop();
}
}
vector<int> result(k);//定义结果数据
//因为结果需要知道前k高的元素,所以需要倒序插入到数组中
for (int i = k - 1; i >= 0; i--) {
result[i] = pri_que.top().first;//插入下标
pri_que.pop();//弹出队列
}
return result;
}
};- 时间复杂度: O(nlogk)
- 空间复杂度: O(n)
?总结:
栈与队列的理论基础:栈先进后出,队列先进先出,无迭代器,底层可以是数组链表队列,都叫容器适配器
用栈实现队列:模拟一下即可,使用两个栈,一个输出栈,一个输入栈,栈与队列不能空操作,其实就需要想明白弹出操作即可,先把输出栈清空,再把输入栈全部压入,弹出
用队列实现栈:也是模拟题,用两个队列实现,一个队列操作,另一个作为辅助队列,其实也是想明白栈的形式原理即可,计算队列的大小,把元素全部放到辅助队列,剩余就是要弹出的元素,在将辅助队列赋值给队列,一个队列也可以实现
有效括号匹配:用栈解决该问题即可,栈可以用来解决对称匹配问题,就是对对碰,考虑清楚不匹配的情况,小技巧:匹配左括号,右括号进栈,最后对比元素是否与栈顶元素相等即可,遇左进栈,遇右弹出比较即可
删除字符相邻重复项:也是消除对称的匹配项,考虑栈来求解即可,最后字符串接收一下,注意字符串的顺序,需要反转一下
逆波兰表达式:其实就是后缀表达式,要知道后缀表达式可以不用考虑运算规则,也是遇到运算符进行消除操作,遇到运算符,将两个元素弹出,做相应的运算符操作即可,再压入栈中,不是运算符需要把字符串转成整形加入栈中,最后栈顶元素就是所求
滑动窗口最大值:需要自己实现一个单调队列,要实现功能:队头元素一直是最大的,这里为何不采用优先级队列,优先级队列可能打乱原本的顺序,所以自己实现一个单调队列即可,如果遍历的元素等于队头元素就从队头弹出,如果遍历的元素大于队尾元素,需要从队尾弹出,直到小于等于队尾元素,此时我们的队头元素就是所求,其实原理就是最大值中再找接下来的局部最大值,之后就是简单的运算,先将k个数字加入,得出来一个结果,在每次弹出一个元素,加入一个元素,即可,这道题很绕,真的值得好好细品!!!!!!!!
前k个高频元素:考的知识点很多:哈希表map,优先级队列,首先需要知道优先级队列,实现大根堆和小根堆区别,此题使用小根堆,我们需要前k高频,不然大根堆是留下低频,priority_queue(需要排序的类型,vector<类型>,规则(自定义)),这里为什么使用map因为需要下标和个数,下标就是key,个数就是value,哈希表进行优先级队里排序取k个元素就是前k个高频元素,这里要注意顺序,队头才是最高频的,所以队列 实现的题都很值得多思考,真的很绕,也容易想不到!!!!!!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 02-python的基础语法-01python字面量/注释/数据类型/数据类型转换
- 【编程语言】协程比较
- PyTorch中常用的工具(3)TensorBoard
- Spring之AOP源码(一)
- 视频格式网络地址转换视频到本地,获取封面、时长,其他格式转换成mp4
- 数据结构:线性表的顺序存储操作(含完整代码,可复制)
- openGauss学习笔记-191 openGauss 数据库运维-常见故障定位案例-出现Error:No space left on device提示
- Java之BigDecimal详解
- 八. 实战:CUDA-BEVFusion部署分析-环境搭建
- 鸿蒙开发已解决-ArkTS开发webview,html页面中的input和按钮等操作均无响应