编译原理笔记（三）

发布时间：2024年01月06日

一、词法分析程序的设计

1、词法分析程序的输出

在识别出下一个单词同时验证其词法正确性之后，词法分析程序将结果以单词符号的形式发送至语法分析程序以回应其请求。

单词符号一般分下列5类：

关键字：如：begin、end、if、while和var。
标识符：如：常量名、变量名和过程名
常数：各种类型的常数，如：25、TRUE和"ABC"等。
运算符：如+、*、<、=等。
界符：如：逗号、分号、括号等、

2、词法分析程序中如何识别单词

常见的可以用于词法规则描述的工具有状态转换图、扩展巴克斯范式（EBNF）、有限状态自动机、正规表达式以及正规文法等。

二、单词的形式化描述工具

1、正规文法

正规文法也称3型文法G={VN，VT，S，P}，其P中的每一条规则都有下述形式：A→aB或A→a，其中A,B $\in$ VN，a $\in$ $VT^{*}$ 。正规文法描述的是VT上的正规集。

2、正规式

设字母表Σ={ $\phi$ ， $\varepsilon$ ，|，.，*，（，）}。
????1）ε和?都是Σ上的一个正规式，它们所表示的正规集为{ε}和?。
????2）任何a∈Σ，a是Σ上的一个正规式，它所表示的正规集为{a}。
????3）假设e1和e2是Σ上的正规式，它们所表示的正规集分别为L(e1)和L(e2)，则
? ? ? ? ·e1|e2是Σ上的正规式，它所表示的正规集为L(e1|e2)= L(e1)∪L(e2)。
? ? ? ? ·e1e2是Σ上的正规式，它所表示的正规集为L(e1e2)= L(e1)L(e2)。
? ? ? ? ·(e1)*是Σ上的正规式，它所表示的正规集为L((e1)*)= L(e1)*。
? ? 4）仅由有限次上述3个步骤而定义的表达式才是Σ上的正规式，仅由这些正规式所表示的符号串的集合才是Σ上的正规集。

?例子：令Σ={a，b}，则有：

? ? ? ? 1）正规式a表示的正规集为{a}。
????????2）正规式a|b表示的正规集为{a，b}。

? ? ? ? 3）正规式ab表示的正规集为{ab}。
? ? ? ? 4）正规式(a|b)(a|b)表示的正规集为{aa，ab，ba，bb}。
? ? ? ? 5）正规式a*表示的正规集为{ε，a，aa，aaa，…}。
? ? ? ? 6）正规式(a|b)*表示的正规集为{ε，a，b，aa，ab，ba，bb，aaa，…}。
? ? ? ? 7）正规式a|a*b表示的正规集为包含字符串a和包含0个或多个a后跟随一个b的所有的符号串。

若两个正规式e1和e2所表示的正规集相同，则说e1和e2等价，写作e1=e2。
设r，s，t为正规式，正规式服从的代数规律如下：
? ? ? ?1）r|s=s|r
? ? ? ?2）r|(s|r)=(r|s)|t
? ? ? ?3）(rs)t=r(st)
? ? ? ?4）r(s|t)=rs|rt，(s|t)r=sr|tr
? ? ? ?5） $\varepsilon$ r=r，r $\varepsilon$ =r
? ? ? ?6）r|r=r

3、正规式转正规文法

字母表Σ上的正规式r到正规文法G-=(VN，VT，S，P)的转换方法为：
????1）选择一个非终结符S生成类似产生式的形式：S $\rightarrow$ r，并将S定为G放识别符号。为表述方便，将S $\rightarrow$ r称作正规式产生式，因为在 $\rightarrow$ 右部中含有“.”，“*”或“|”等正规式符号，不是V中的符号。
????2）若x和y都是正规式，对形如A $\rightarrow$ xy的正规式产生式，重写成A $\rightarrow$ xB，B $\rightarrow$ y两个产生式，其中B是新选择的非终结符。

例：对于r=a(a|d)*

? ? ? ? 首先形成S $\rightarrow$ a(a|d)*，然后形成S $\rightarrow$ aA和A $\rightarrow$ (a|d)*，在形成

? ? ? ? S $\rightarrow$ aA? ? A $\rightarrow$ (a|d)B

? ? ? ? A $\rightarrow$ $\varepsilon$ ? ? B $\rightarrow$ {a|d)B

? ? ? ? B $\rightarrow$ $\varepsilon$

4、正规文法转正规式

	文法产生式	正规式
规则1	A $\rightarrow$ xB? ? B $\rightarrow$ y	A=xy
规则2	A $\rightarrow$ xA\|y	*A=xy**
规则3	A $\rightarrow$ x? ? A $\rightarrow$ y	A=x\|y

例如：文法G[S]如下：

S $\rightarrow$ aA? ? ? ? S $\rightarrow$ a? ? ? ? A $\rightarrow$ aA? ? ? ? A $\rightarrow$ dA? ? ? ? A $\rightarrow$ a? ? ? ? A $\rightarrow$ d

解：首先有

? ? ? S=aA|a

? ? ? A=(aA|dA)|(a|d)

? ? ? ?再将A的正规式变换成A=(a|d)A|(a|d)，又变换为A=(a|d)*(a|d)，再代入S得：

? ? ? S=a(a|d)*(a|d)|a

? ? ? 再利用正规式的代数变换可依此得到

? ? ? ?S=a(a|d)*(a|d)| $\varepsilon$

? ? ? ?S=a(a|d)*?

三、有穷自动机

1、确定的有穷自动机

1.定义：一个确定的有限自动机(DFA) M是一个五元组：M=(K，Σ，f，S，Z)，其中：
????1）K是一个有限集，它的每一个元素称为一个状态。
????2）Σ是一个有穷字母表，它的每个元素称为一个输入字符。
????3）f是一个转换函数，是K $\times$ Σ $\rightarrow$ K上的映像。
????4）S∈K，是唯一的初态。
????5）Z?S，F是一个终态集，可以为空。?
2.DFA的状态转移矩阵
????????DFA可用一个二维矩阵表示，矩阵的行表示状态，列表示输入字符，矩阵元素表示δ(s，a)的值。
3.DFA是状态转换图
????????若设DFA M含有m个状态和n个输入字符，则这个图含有m个状态结点，每个结点至多有n条箭弧射出与其它的状态结点相连接，每个箭弧用Σ中的一个不同输入字符作为标记。整张图含有唯一的初态结点和若干终态结点。

例子：设DFA M=({0,1,2,3}，{a,b}，δ，{3})，其中，δ定义为：
????????δ(0，a)=1，δ(0，b)=2，δ(1，a)=3，δ(1，b)=2，δ(2，a)=1，δ(2，b)=3，δ(3，a)=3，δ(3，b)=3。

4.DFA的识别字符串
????????1）对Σ上的任何符号串w∈Σ*，若存在一条从初态结点到某一终态结点的通路，且该通路上所有弧的标记符连接成的字符串等于w，则称w可被DFA M所识别。若M的初态结点同时又是终态结点，则空字符串ε被M所识别。
?????????2）DFA与语言的关系：DFA M所能识别的符号串的全体记为L(M)。

2、不确定的有穷自动机

1.定义：一个不确定有限自动机(NFA) M是一个五元组：M=(S，Σ，δ，S0，F)，其中：
????1）S是一个有限集，它的每一个元素称为一个状态。
????2）Σ是一个有穷字母表，它的每个元素称为一个输入字符。
????3）δ是一个从S×Σ到S的子集的映射，即δ：S×Σ*→2S
????4）S0?S，S0是一个非空初态集。
????5）F ?S，F是一个终态集，可以为空。
2.NFA的状态转换图
????若设NFA M含有n个状态和m个输入符号，则这个图含有n个状态结点，每个结点可射出若干箭弧与其它的状态结点相连接。对于w∈{ε}∪Σ，若δ(q0，a)={q1，q2，…，qk}(k≥0)，则从q0出发，分别到q1，q2，…，qk的k条弧，弧上均标记为a。整张图含有唯一的初态结点和若干终态结点。
3.NFA识别字符串
????1）对Σ*上的任何符号串，若存在一条从某一初态结点到某一终态结点的通路，且该通路上所有弧的标记符号依次连接成的字符串等于w，则称w可被NFA M所识别。若M的某些结点同时又是终态结点，则空字符串ε被M所识别。
????2）NFA与语言的关系：Σ*中所有可被NFA M所识别的符号串的集合记为L(M)。
4.DFA和NFA的关系
????1）DFA是NFA的特例，NFA是DFA概念的推广。
????2）NFA能识别的语言都能被一个DFA识别。
????3）DFA相对NFA的识别程序更容易实现。

3、NFA转换为等价的DFA

1.NFA的确定化：对任给的NFA M。都能相应地构造一个DFA M‘，使得L(M’)=L(M)。
2.NFA的子集法：DFA的每一个状态代表NFA状态集合的某个子集，构造的DFA使用它的状态去记录NFA读入输入符号之后可能到达的所有状态的集合。
3.状态集合I的a弧转换，表示为ε-Closure(I)，定义为一个状态集，是状态集I中的一组任何状态S经任意条ε弧而能够到达的状态的集合。
4.状态集合I的a弧转换，表示为move(I，a)，定义为状态集合J，其中J是所有那些可以从I中的某一状态经过一条a弧而到达的状态的全体。

4、确定有限自动机的化简

1.化简的目的：去除多余或等价的状态，降低存储代价，提高句子识别的效率。
2.有限自动机的多余状态：从初态出发，任何可识别的输入串也不能到达的状态。
3.状态等价：在两个状态s和t等价的条件是以下两个：
? ? ? ? 一致性条件--状态s和t必须同时为可接受状态或不可接受状态。
? ? ? ? 蔓延性条件--对于所有输入符号，状态s和状态t必须转换到等价的状态里。
4.DFA的化简（分割法）：
?????????i）将DFA M的状态集S划分为两个子集；终态集F和非终态集F ?，形成初始划分Π。
????????ii）对Π建立新的划分Πnew。对Π中的每个状态子集G进行如下变换：
????????????a）把G划分成新的子集，使G的两个状态s和t属于同一个子集，当且仅当对任何输入符号a，状态s和t转换到的状态都属于Π的同一子集。
????????????b）用G划分出的所有新子集替换G，形成新的划分Πnew。
????????iii）若Πnew和Π相等，则执行第iv）步，否则，令Π=Πnew，重复第ii）步。
????????iv）划分结束后，对划分中的每个状态子集，选出一个状态作为代表，删去其它一切等价的状态，并把射向其它状态的箭弧改为射向这个代表的状态。

四、正规式与有限自动机之间的等价性

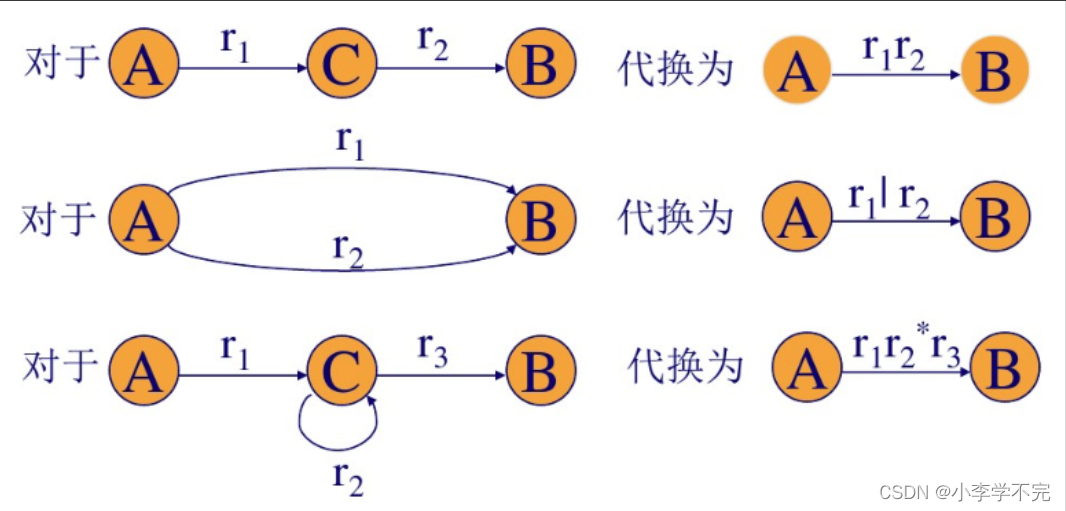
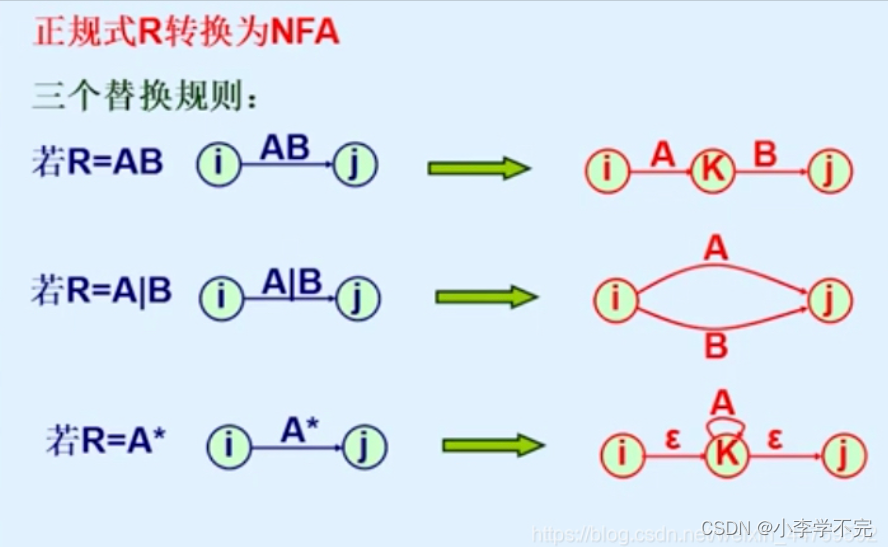
1.由正规式构造有限自动机??
消去结点的规则如下：

文章来源:https://blog.csdn.net/lerp020321/article/details/134937575
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！