通信入门系列——连续卷积定理、循环卷积、离散卷积定理

本节目录

一、连续卷积定理
1、时域卷积定理
2、频域卷积定理
二、循环卷积
三、离散卷积定理

本节内容
一、连续卷积定理
卷积定理在信号分析中占有重要的地位，包括时域卷积定理和频域卷积定理。在信号分析领域，通常采用基于卷积定理的时频域分析，来作为信号处理方法。
1、时域卷积定理
时域信号x1(t)与频域信号X1(ω)为傅里叶变换对，时域信号x2(t)与频域信号X2(ω)为傅里叶变换对，那么x1(t)*x2(t)的傅里叶变换为X1(ω)×X2(ω),这就是时域卷积定理，在时域的两个函数的卷积，等于其对应频域的乘法。

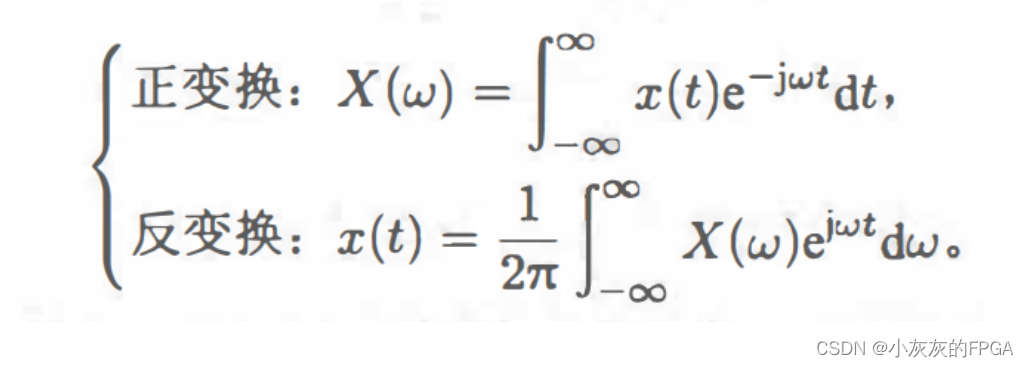
如何证明时域卷积定理？

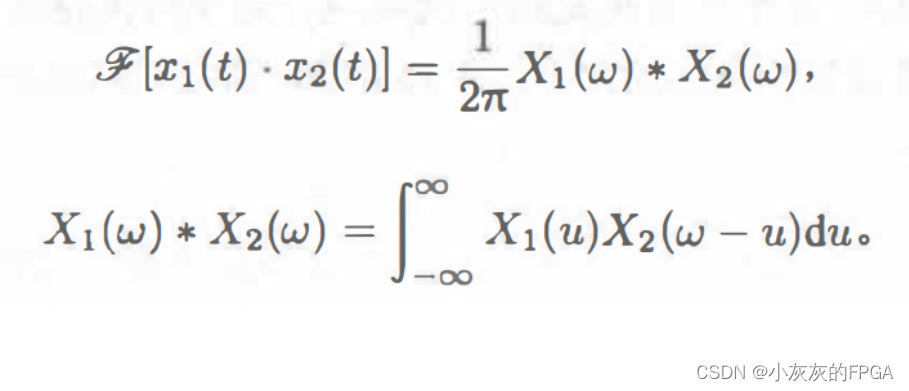
2、频域卷积定理
频域卷积定理，频域的两个信号的卷积，在时域变成了乘积。

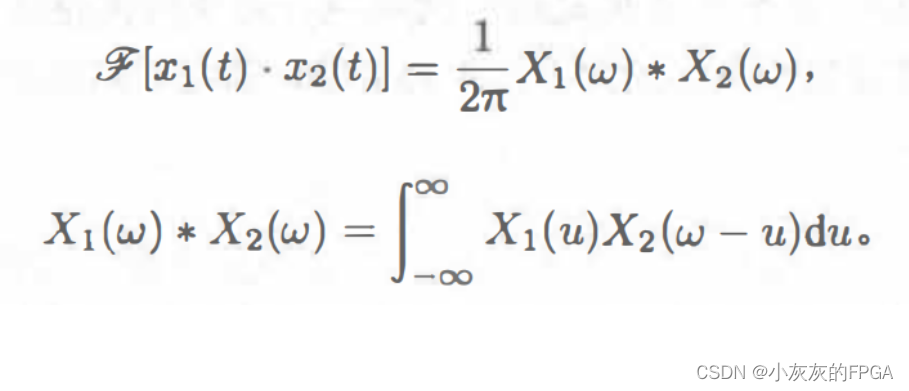
二、循环卷积
一个离散系统的冲激响应为h[n],输入信号为x[n]，对应的输出信号y[n]是x[n]与h[n]的卷积，这个卷积称为线卷积。若一个系统的输入信号是周期为N的信号x[n],那么在系统达到稳态后，系统的输出y[n]也是周期为N的信号。
周期为N的周期信号x[n],经过系统h[n],输出信号为y[n]。把周期输入信号x[n]分解为多个信号的和，每个信号是x[n]的一个周期，并对应产生一个输出信号，根据线性系统的性质，输出的周期信号就是这些单一输出信号的叠加。在此过程中，系统的冲激响应h[n]也应该进行切段并累加，得到一个长度为N的有限长度序列，如果长度小于N,进行补零操作得到长度为N的序列。

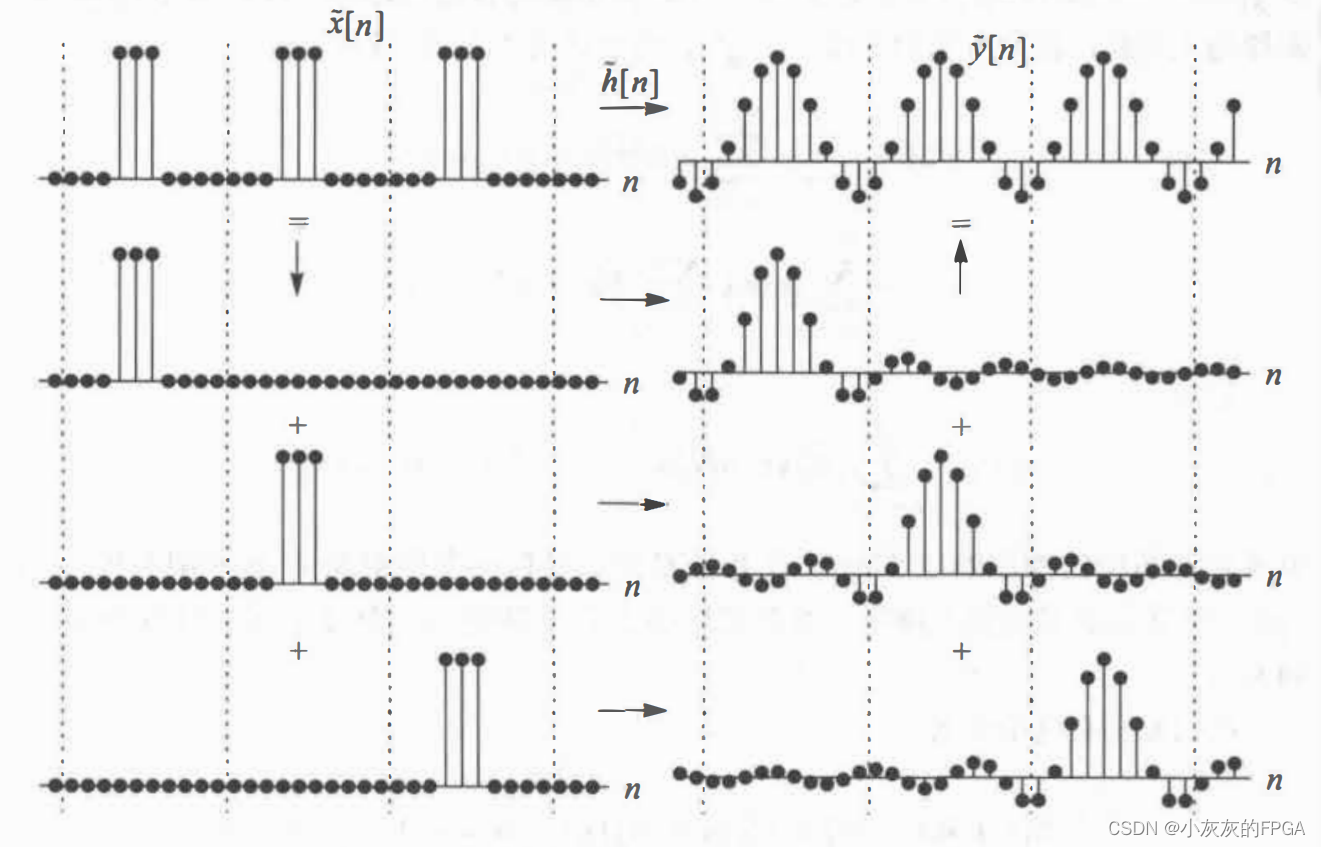
循环卷积，要求两个序列的长度相等，输出信号的一个周期，是输入信号的一个周期和一个同等长度的序列循环卷积。序列是由信号的冲激响应分段累加或者补零后得到的通道长度的序列。
三、离散卷积定理
连续信号的卷积定理是时域下的卷积对应频域的乘积。而离散信号的卷积定理，使用的是循环卷积。

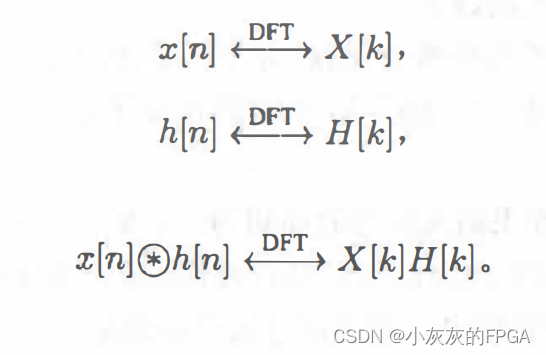
如何理解并证明离散卷积定理？

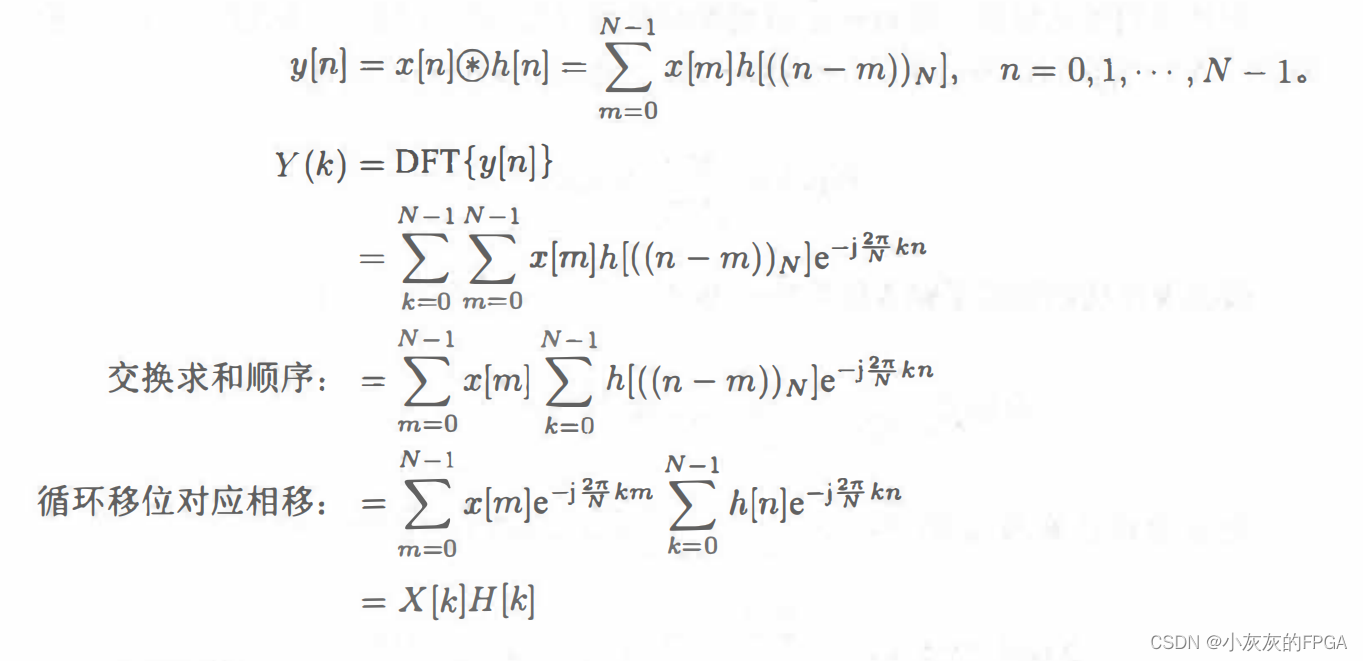
离散系统的响应，输入和输出都是周期信号，输出信号的一个周期是输入信号的一个周期与一个等长序列的循环卷积。系统的冲激响应，通过分段累加和补零得到与输入信号周期长度相同的序列。在频域中，Y(k)=X[k]H[K]，两者是相乘的关系，其中H[k]是系统的频率特性，可以用幅值和相位来表示：

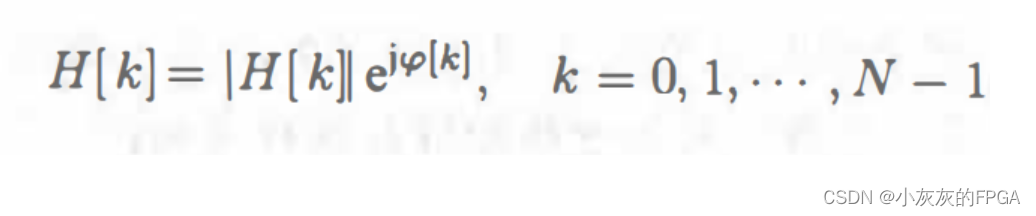
上式中|H[k]|表示幅频特性，ψ[k]表示相频特性。其实系统的响应是对输入信号当中的频率k进行幅度的增益和相位的改变。