回溯(dfs)题集(1)
发布时间:2024年01月01日
在这里主要是记录我Leetcode刷题所写的代码
78子集
class Solution {
// 存储结果的列表,每个子列表代表一种子集
List<List<Integer>> ans = new ArrayList<>();
// 临时存储当前子集的列表
List<Integer> re = new ArrayList<>();
// 主方法,返回给定数组的所有子集
public List<List<Integer>> subsets(int[] nums) {
// 调用深度优先搜索方法
dfs(nums, 0);
// 返回所有子集
return ans;
}
// 深度优先搜索方法,使用回溯的思想来生成所有可能的子集
public void dfs(int[] nums, int start) {
// 将当前子集添加到结果列表中
ans.add(new ArrayList<>(re));
// 如果已经遍历完数组,则返回(相当于递归的结束条件)
if(start >= nums.length) return;
// 从当前位置开始遍历数组
for(int i = start; i < nums.length; i++) {
// 将当前元素添加到临时子集中
re.add(nums[i]);
// 继续递归,从下一个位置开始遍历
dfs(nums, i + 1);
// 回溯,移除临时子集中的最后一个元素,尝试其他可能的组合
re.removeLast();
}
}
}
17 电话号码的字母组合
class Solution {
// 存储结果的列表,每个字符串代表一种组合
List<String> ans = new ArrayList<>();
// 输入的数字字符串长度
int n;
// 临时存储当前组合的字符串
StringBuffer sb = new StringBuffer();
// 主方法,返回给定数字字符串的所有字母组合
public List<String> letterCombinations(String digits) {
// 如果输入为空,则直接返回结果列表
if(digits.length() == 0) return ans;
// 定义一个字符串数组,每个数字对应一个字母集合
String[] numstring = {"", "","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
// 调用深度优先搜索方法
dfs(0, numstring, digits);
// 返回所有字母组合
return ans;
}
// 深度优先搜索方法,使用回溯的思想来生成所有可能的字母组合
public void dfs(int idx, String[] numstring, String digits) {
// 如果当前组合的长度等于输入数字字符串的长度,则将组合添加到结果列表中
if(sb.length() == digits.length()) {
ans.add(new String(sb));
return;
}
// 获取当前数字对应的字母集合
String now = numstring[digits.charAt(idx) - '0'];
// 遍历当前字母集合中的每个字母,并递归调用dfs方法
for(int i = 0;i < now.length();i ++) {
sb.append(now.charAt(i)); // 将当前字母添加到临时组合中
dfs(idx + 1, numstring, digits); // 递归调用,处理下一个数字字符
sb.deleteCharAt(sb.length() - 1); // 回溯,移除临时组合中的最后一个字母,尝试其他可能的组合
}
}
}
39组合总和
这是我一开始写的代码:
class Solution {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> re = new ArrayList<>();
boolean[] state;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
state = new boolean[candidates.length + 1];
dfs(candidates, target, 0);
return ans;
}
public void dfs(int[] candidates, int target, int now) {
if(now == target) {
ans.add(new ArrayList<>(re));
return;
} else if(now > target) {
return;
}
for(int i = 0;i < candidates.length;i ++) {
if(!state[i]) {
now += candidates[i];
re.add(candidates[i]);
// state[i] = true;
dfs(candidates, target, now);
now -= candidates[i];
re.removeLast();
// state[i] = false;
}
}
}
}
但是测试用例是这样的:
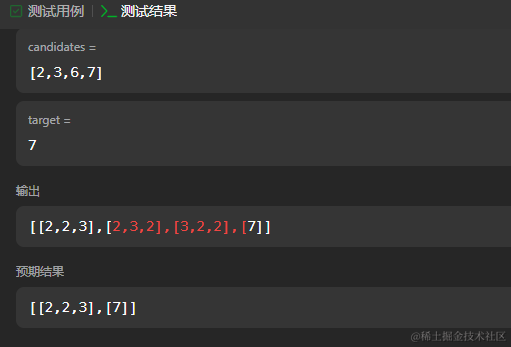
也就是说我实现了排列,但是没实现组合,看了题解,还是没从当前位置继续遍历的问题
class Solution {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> re = new ArrayList<>();
boolean[] state;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
// Arrays.sort(candidates);
state = new boolean[candidates.length + 1];
dfs(candidates, target, 0, 0);
return ans;
}
public void dfs(int[] candidates, int target, int now, int start) {
if(now == target) {
ans.add(new ArrayList<>(re));
return;
} else if(now > target) {
return;
}
for(int i = start;i < candidates.length;i ++) {
now += candidates[i];
re.add(candidates[i]);
dfs(candidates, target, now, i);
now -= candidates[i];
re.removeLast();
}
}
}
22 括号生成
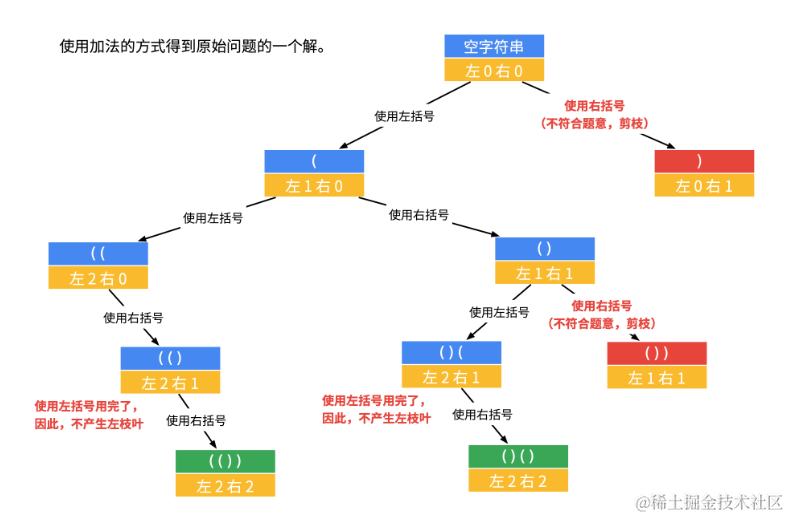
感谢题解里liweiwei1419的思路解答,我知道肯定用dfs进行搜索,可是不知道如何匹配,这个就教会我如何匹配了,因为知道用dfs其实就是套模板了,但是要知道如何去匹配这个。
class Solution {
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList<>();
if(n == 0) return ans;
dfs("", 0, 0, n, ans);
return ans;
}
public void dfs(String s, int left, int right, int n,List<String> ans) {
if(left == n && right == n) {
ans.add(s);
return;
}
// 不符合条件退出, 剪枝
if(left < right) return;
// 先左边
if(left < n) {
dfs(s + '(', left + 1, right, n, ans);
}
// sb.deleteCharAt(sb.length() - 1);
if(right < n) {
dfs(s + ')', left, right + 1, n, ans);
}
}
}
79 单词搜索
class Solution {
String target;
int m,n;
public boolean exist(char[][] board, String word) {
target = word;
m = board.length;
n = board[0].length;
for(int i = 0;i < m;i ++) {
for(int j = 0;j < n;j ++) {
if(dfs(board, i, j, 0)) {
return true;
}
}
}
return false;
}
public boolean dfs(char[][] board, int x, int y, int idx) {
if(x >= m || x < 0 || y >= n || y < 0 || board[x][y] != target.charAt(idx)) return false;
if(idx == target.length() - 1) return true;
// 利用回溯,所以要设置一个temp值
char temp = board[x][y];
board[x][y] = '.';
// 遍历周围
boolean b = (dfs(board, x, y + 1, idx + 1) || dfs(board, x, y - 1, idx + 1) ||
dfs(board, x + 1, y, idx + 1) || dfs(board, x - 1, y, idx + 1));
board[x][y] = temp;
return b;
}
}
文章来源:https://blog.csdn.net/m0_51547272/article/details/135325662
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!