30、共空间模式CSP与白化矩阵
发布时间:2024年01月02日
CSP算法和PCA降维都涉及到了白化,那白化的目的和作用到底是啥呢?
矩阵白化目的:
对于任意一个矩阵X,对其求协方差,得到的协方差矩阵cov(X)并不一定是一个单位阵。
下面介绍几个线代矩阵的几个概念:
1、单位阵:
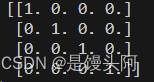
对角线特征值全为1的矩阵,记为E
2、对角阵:
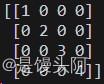
所以,单位阵一定是对角阵,反之,错
3、对称阵:

矩阵A(i,j)=A(j,i)为对称阵,所以协方差矩阵是对称阵,但不一定是对角阵,更别提是单位阵
所以:
矩阵白化就是找到一个变换阵P,使得Y=PX的协方差矩阵cov(Y)是一个单位阵。
因为通过矩阵白化后,协方差变为单位阵,矩阵白化的目的就是:
使被变换的矩阵经过其向量的方差相同(单位阵性质),最后的问题便是如何找到这个变换矩阵P
4、矩阵白化推导:
上面提到,对于矩阵X,协方差矩阵cov(X)=XXt并不一定是对角阵,但是对于实对称(对称矩阵A的所有值为实数,实对称阵必可以相似对角化)的协方差矩阵,特征值可以被分解为:
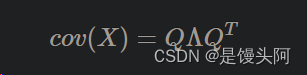
其中:
Λ=特征值组成的对角阵,Q=对应的特征向量。是正交阵(Q中存在两个向量相乘为0)
现在要找到线性变换矩阵P,使得Y=PX的协方差矩阵可以成为单位阵E,
即:
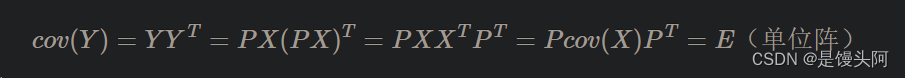
现在令:

有:
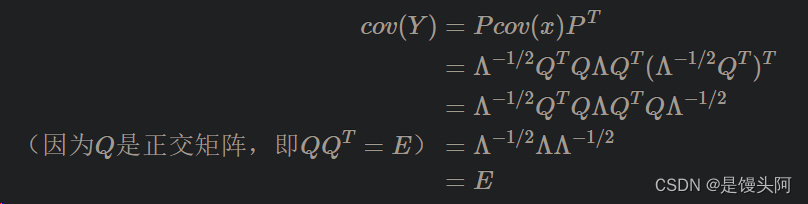
所以,当

可以使得Y=PX的协方差矩阵为单位阵E
因此 ,通过矩阵白化后,矩阵Y的各个向量(列向量还是行向量根据上文确定)之间就不相关了。
对于CSP,得出矩阵P之后,就可以用了构建空间滤波器了:
对于类别1:E1,有滤波器S1:

对于类别2:E2,有滤波器S2:

文章来源:https://blog.csdn.net/mantoudamahou/article/details/135333011
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!