何为算法之空间复杂度
前言
不知前面所讲的算法的十大特征你是否记住了呢?其实除了这十大特征之外,算法还有两个衡量标准。
不同的问题需要使用不同的算法作为策略,不同的算法也可能占用不同的时间和空间来完成相同的任务,这时候,对算法的选择显得至关重要。一个算法的质量优劣将直接影响整个程序的运行效率。
算法分析的目的是选择合适的算法,并对算法进行改进。如何衡量一个算法的优劣呢?其标准是空间复杂度(Space Complexity)与时间复杂度(Time Complexity)。
什么是空间复杂度
一个算法所占用的存储空间包括三个方面:算法本身所占用的空间、输入/输出数据所占用的空间,以及算法运行所占用的空间。
1.算法本身所占用的空间
算法本身所占用的空间即程序代码区,用于存放算法程序的二进制代码,与程序的代码行数和各行长度相关。例如以下两段代码,它们实现的功能是一样的,但代码1所占用的空间明显比代码2要多一些。
代码1
#输出1~10中3的倍数
#定义test函数:输入任何列表,返回列表中3的所有倍数
def test(x):
list1 = []
for i in x:
if i % 3 == 0: # %是取余运算
list1.append(i)
return list1
#调用test函数计算1~10中3的倍数
print(test(list(range(1,10))))

输出结果

代码2
#使用lambda函数
print(list(filter(lambda x: x % 3 == 0 ,range(1,10))))
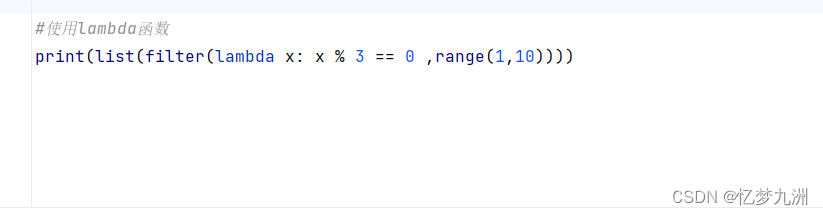
输出结果

注意
由于算法本身所占用的空间很小,所以我们一般不做深究。
2. 输入/输出数据所占用的空间
输入/输出数据所占用的空间主要是指问题所调用的数据所占用的空间,跟算法没有关系。
3. 算法运行所占用的空间
算法运行所占用的空间就反映算法的空间复杂度,它是算法运行时所消耗的内存空间的量度,记作:
S
(
n
)
=
O
(
f
(
n
)
)
S(n)=O(f (n))
S(n)=O(f(n))
常见的空间复杂度有 O(1)、0(n)和
O
(
n
2
)
O(n^2)
O(n2)等。
它们分别代表什么意思呢?很简单,当算法运行时占用的临时空间不随某一变量n的改变而改变时,即空间复杂度为常量,表示为 O(1)。同理,当算法运行时占用的临时空间随n的改变而改变时,空间复杂度即O(n);当算法运行时占用的临时空间随n^2的改变而改变时,空间复杂度则为
O
(
n
2
)
O(n^2)
O(n2)以此类推。
用代码来表示空间复杂度,这对于 Python 来说简直太容易了。

注意
空间复杂度是算法运行时所占用空间的一个量度,而不是计算具体的占用空间。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- IDEA版SSM入门到实战(Maven+MyBatis+Spring+SpringMVC) -Spring中自动装配和中注解
- C语言初学函数(练习)
- 【通知】我的教学文章《Rust跟我学》已全部上线
- 建议收藏!上位机编程学习经验分享
- 这个AI模型能识别出这个橘子吗?
- Java8新特性总结
- 基于微信小程序的音乐平台 JAVA简易版
- 雍禾医疗完善毛发医疗产业链 雍禾植发引领行业创新
- Leetcode 63 不同路径 II
- 前端实现搜索功能