python数字图像处理基础（八）——harris角点检测、图像尺度空间、SIFT算法

harris角点检测

原理

Harris 角点检测是一种用于在图像中检测角点的算法。角点是图像中局部区域的交叉点或者突出的特征点。Harris 角点检测算法旨在寻找图像中对于平移、旋转和尺度变化具有不变性的角点。

该算法通过计算图像中每个像素点的灰度值的变化，来识别角点。具体来说，Harris 角点检测通过以下步骤实现：

1. 计算图像的梯度： 对图像进行空间梯度的计算，通常使用 Sobel 等滤波器。

2. 计算结构矩阵： 对每个像素点，根据其周围像素的梯度计算一个结构矩阵。结构矩阵是一个2x2的矩阵，其中包含了该像素点附近局部梯度的信息。

3. 计算角点响应函数： 利用结构矩阵的信息，计算每个像素点的角点响应函数。Harris 角点检测使用如下的角点响应函数：

$$R=\det (M)?k?{\text{trace}}^2(M)$$

其中，M是结构矩阵，$\det$表示矩阵的行列式，$\text{trace}$ 表示矩阵的迹，k是一个常数（通常取较小的值）。

4. 选取角点： 通过对角点响应函数进行阈值处理，选择角点。通常，角点响应函数大于某个阈值的像素点被认为是角点。

Harris 角点检测的优势在于它对图像的平移、旋转和尺度变化有较好的不变性，因此在计算机视觉领域中被广泛应用。检测到的角点通常用于图像匹配、物体识别、图像配准等应用。

对于角点的检测，harris依据一下直观判断：角点应该在窗口的各个方向都有变化，边界会在某个方向基本不变，而平坦区域在各个方向变化都小。

函数

cv2.cornerHarris(src, blockSize, ksize, k, dst, borderType)

• src：数据类型为float32的输入图像
• blockSize：角点检测中要考虑的领域大小
• ksize：Sobel求导中使用的窗口大小
• k：Harris 角点检测方程中的自由参数，取值参数为 [0,04，0.06].
• dst：目标图像
• borderType：边界类型

import cv2
import numpy as np
from matplotlib import pyplot as plt
 
 
def plot(img, n):
    filename = img
    #读入图像并转化为float类型，用于传递给harris函数
    img = cv2.imread(filename)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    gray = np.float32(gray)
    # 输入图像必须是 float32 
    
    #对图像执行harris,最后一个参数在 0.04 到 0.05 之间
    dst = cv2.cornerHarris(gray, 2, 3, 0.04)
    
    # result is dilated for marking the corners, not important(腐蚀harris结果)
    dst = cv2.dilate(dst, None)
    
    # Threshold for an optimal value, it may vary depending on the image.(设置阈值)
    Threshold = 0.005*dst.max()
    img[dst > Threshold] = [255, 0, 0] # RGB，[0,0,255]表示该点为红色
    
    # 打印图像
    plt.subplot(1, 3, n), plt.imshow(img, cmap='gray'),
    plt.title('dst'), plt.axis('off')
 
 
plot('test30.jpg', 1)
plot('test30_1.jpg', 2)
plot('test30_2.jpg', 3)
 
plt.show()

# 一般方法
import cv2
import numpy as np


img = cv2.imread('./image/img2.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
dst = cv2.cornerHarris(gray, 2, 3, 0.04)

img[dst > 0.1 * dst.max()] = [0, 0, 255]
cv2.imshow('dst', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

---

图像尺度空间

概念

尺度空间就是试图在图像领域中模拟人眼观察物体的概念与方法。

这是由于通过计算机视觉系统，我们无法直接获取所关注物体、对象的大小，这时候就需要一个尺度空间来描述。

在一定的范围内，无论物体是大还是小，人眼都可以分辨出来。然而计算机要有相同的能力却不是那么的容易，在未知的场景中，计算机视觉并不能提供物体的尺度大小，其中的一种方法是把物体不同尺度下的图像都提供给机器，让机器能够对物体在不同的尺度下有一个统一的认知。在建立统一认知的过程中，要考虑的就是在图像在不同的尺度下都存在的特征点。

使之能在图像模糊的时候能识别出来是什么东西（教室里看到的清晰的班主任和球场上可以认出走过来的模糊人脸是班主任）

二维图像的尺度空间定义

局部不变性

对于目标物体，我们希望通过一些特征来描述它。比如车，可以选取车牌、轮廓等特征，对于人脸，则有五官、面型等特征。

分析图像物体时，我们关注的是目标与背景的差异性，局部不变性就是特征分析的重要性质。其包括：

• 尺度不变性

  摄像头相对于物体远近呈现出来的物体尺寸不受其大小影响。 貌似说：就是不管你的物体大小如何，摄像头都可以改变目标物体的图像大小，只不过是摄像头放的远近问题。比如说：两个除了尺寸之外都一样的球，摄像头离大的球远一些，离小的球近一些，在某个点上，就会出现图像上两个球一样大小的情况。

• 旋转不变性

  即若图像按下式进行变换（相当于所有坐标在极坐标下旋转θ角度）：

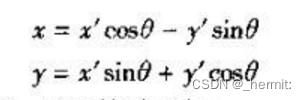
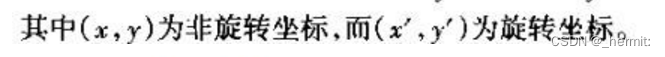
图像的某些特征值不变，（某些函数值不变，如hu矩）

当这个物体发生旋转时，我们照样可以正确地辨认它，这就是所谓的旋转不变性(另外一个熟悉的具有旋转不变形的是拉普拉斯算子)

局部不变特征

全局特征：从整个图像中抽取的特征。较多的运用在图像检索领域，如图像颜色直方图。

局部特征：从图像的局部区域中抽取的特征（这个局部区域往往是图像中的一个像素及它周围的邻域）。

一种好的局部特征应该具有下面的特性：

• 可重复性：同一个物体在不同时间，不同角度拍到图像中，检测到的特征对应的越多越好。
• 独特性：特征在该物体上表现为独特性，能与场景下其他物体区分。
• 局部性：特征往往是物体某个局部的特点，这样才可以避免遮挡时不能匹配的问题。
• 数量性：检测到的特征数目一定要多，密集度最好能在一定程度上反映图像的内容。
• 准确性：得到的特征应该能被精确定位，能够精确到像素。
• 高效性：特征检测算法运算要快。

为了研究图像的尺度不变特征，我们需要先从图像的尺度空间理论开始。

当用一个机器视觉系统分析未知场景时，计算机没有办法预先知识图像中物体尺度，因此，我们需要同时考虑图像在多尺度下的描述，获知感兴趣物体的最佳尺度。

所以在很多时候，我们会在将图像构建为一系列不同尺度的图像集，在不同的尺度中去检测我们感兴趣的特征。比如：在Harr特征检测人脸的时候，因为我们并不知道图像中人脸的尺寸，所以需要生成一个不同大小的图像组成的金字塔，扫描其中每一幅图像来寻找可能的人脸

SIFT算法

SIFT（Scale-Invariant Feature Transform）是一种用于图像处理和计算机视觉中的特征提取算法，它具有尺度不变性和旋转不变性，因此在图像匹配、目标识别和图像配准等领域得到广泛应用。

SIFT 算法的主要步骤包括：

1. 尺度空间极值检测： 在不同的尺度下，通过高斯滤波器构建图像的尺度空间金字塔，然后在每个尺度下检测局部极值点（关键点）。这些关键点代表图像中的显著特征。

2. 关键点定位： 在检测到的极值点中，通过比较其尺度空间的局部邻域，选择稳定的关键点。这些关键点具有在尺度、位置和方向上的不变性。

3. 方向分配： 为每个关键点分配主方向，使得该关键点对于旋转具有不变性。SIFT 使用梯度方向直方图来确定关键点的主方向。

4. 关键点描述： 使用关键点周围的图像信息来创建描述符。描述符是一个向量，包含关键点周围区域的梯度信息。这些描述符是用于匹配关键点的特征。

SIFT 算法的优点包括对于尺度、旋转、光照变化等的不变性，以及对于局部图像区域的高判别性。然而，由于 SIFT 的计算量较大，因此在实时性要求较高的应用中可能会受到一些限制。

要点：

检测到关键点 —(种子、直方图统计)—> 生成特征向量

让选择的特征点更加准确：把图像首先做一个金字塔，金字塔中每一层做不同的高斯滤波，让每一层图像进行不同程度的模糊，通过差分的方法选出最有价值的点，点的选择方法：DoG空间极值检测——在3X3的三维像素区域内(类似魔方)将中心点与周围26个像素点进行比较，得到候选关键点；但这些点是DOG空间的局部极值点，而且均为离散的点。故需要对这些点做曲线拟合操作，计算其极值点，从而实现关键点(特征点)的精确定位。补充完善：消除边界响应（Hessian矩阵）

得到特征点坐标后，接着要获取特征点的主方向，要先算出每个点坐标Location(x,y)的梯度的模m(x,y)以及方向θ(x,y),完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向，生成特征描述；为保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标旋转θ角度，即将坐标轴旋转为特征点的主方向；旋转之后以主方向为中心取8X8的窗口，求每个像素的梯度幅值和方向，找到一些种子点，基于这些种子，算出每一小块的直方图(8维向量)，最终得到16X8=128维的向量。这样一个关键点就会产生128维的SIFT特征向量。

import cv2


img = cv2.imread('./image/img1.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
sift = cv2.xfeatures2d.SIFT_create()
# 注：新版本(对应py3.9)为sift = cv2. SIFT_create()


kp = sift.detect(gray, None)
# 找到关键点

img = cv2.drawKeypoints(gray, kp, img)
# 绘制关键点

cv2.imshow('sp',img)
cv2.waitKey(0)

---