图论算法（数学建模）算法以后更新

无权值，无向，当成1就行

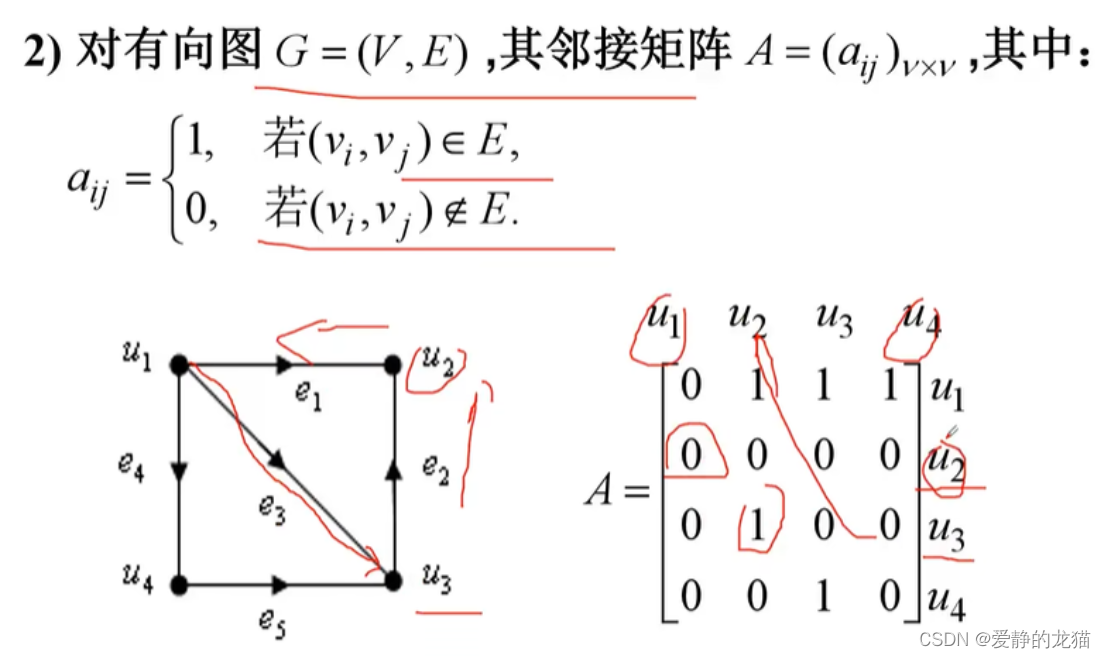
有向

有向赋权

顶点度的概念

Dijkstra算法

?Dijkstra算法能求-一个顶点到另一-顶点最短路径。它是由Di jkstra于1959年提出的。实际它能出始点到其它所有顶点的最短路径Dijkstra算法是一种标号法:给赋权图的每一一个顶点记一个数，称为顶点的标号(临时标号，称T标号，或者固定标号，称为P标号)。T标号表示从始顶点到该标点的最短路长的上界; P标号则是从始顶点到该顶点的最短路长。

迪杰斯特拉算法采用贪心算法的策略，将所有顶点分为已标记点和未标记点两个集合，从起始点开始，不断在未标记点中寻找距离起始点路径最短的顶点，并将其标记，直到所有顶点都被标记为止。?需要注意的一点是该方法不能处理带有负权边的图，下面我们举出一个实例并通过迪杰斯特拉方法对其进行求解。

• 可以求解图的最短路径问题，单源最短路径问题求解
• 例如：

1. 从A地到B地的最短路径

function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
   if i~=start
       label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
   for i=1:n
      ins=0;
      for j=1:length(s)
         if i==s(j)
            ins=1;
         end,  
      end
      if ins==0
         v=i;
         if label(v)>(label(u)+w(u,v))
            label(v)=(label(u)+w(u,v)); 
         f(v)=u;
         end, 
      end, 
   end   
v1=0;
   k=inf;
   for i=1:n
         ins=0;
         for j=1:length(s)
            if i==s(j)
               ins=1;
            end, 
         end
         if ins==0
            v=i;
            if k>label(v)
               k=label(v);  v1=v;
            end,  
         end,  
   end
   s(length(s)+1)=v1;  
   u=v1;
end
min=label(terminal); path(1)=terminal;
i=1; 
while path(i)~=start
      path(i+1)=f(path(i));
      i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

还有弗洛伊德算法

采用动态规划的方法编写