现代雷达车载应用——第3章 MIMO雷达技术 3.3节 汽车MIMO雷达测角

????????经典著作，值得一读，英文原版下载链接【免费】ModernRadarforAutomotiveApplications资源-CSDN文库。???

3.3 汽车MIMO雷达测角

?????? 在发射天线和接收天线分别为Mt和Mr的汽车MIMO雷达中，可以合成一个由Mt*Mr个阵元组成的虚拟ULA，单元间距为d。阵列响应可以写作：

??????????(3.5)

????????这里时虚拟阵列导向矩阵，且

??????????(3.6)????????????????????

????????这里，n是噪声项，，βk为第k个目标的目标反射系数。阵列在特定时间实例的响应由所有虚拟接收机获得的数据组成，对应于相同的距离-多普勒单元，定义为阵列快照。在高动态的汽车场景中，通常只有少量的阵列快照，在最坏的情况下甚至只有单个快照可用[22]。

????????在具有虚拟ULA的汽车MIMO雷达中，可以通过数字波束形成(DBF)[23-25]对在阵列单元上拍摄的快照做FFT，即(3.16)中的y(见图3.6)。DBF可以在嵌入式DSP中通过单个快照有效地实现。然而，DBF并不是一种高分辨率的测角方法。基于子空间的方法，如MUSIC[26]和ESPRIT[27-30]，基于稀疏感知的方法[31-39]，或[40]和[41]的迭代自适应方法(IAA)，可以实现更高分辨率的测角。基于子空间的测角方法的性能依赖于多快照阵列协方差矩阵的准确估计，这在高度非平稳的汽车雷达场景中是一项具有挑战性的任务。在这种情况下，应用空间平滑[42]引入虚拟快照进行阵列协方差矩阵估计。虽然基于稀疏感知的方法和IAA具有较高的计算成本，但它们产生基于单个快照的角度估计，这对于快照限制的汽车雷达非常重要。

????????使用d=λ/2的ULA实现L4和L5级自动驾驶要求的高角度分辨率是非常昂贵的。根据文献[43]，孔径尺寸为D的天线阵3dB波束宽度为，要达到1度的3dB波束宽度，天线阵孔径应为D=51λ左右。如果天线阵列为单元间距为半波长的ULA，则应由大约100个阵列单元组成。即使借助MIMO雷达技术，合成这种半波长单元间距的大型虚拟ULA的成本也非常高。在不牺牲高角分辨率的情况下进一步降低成本的一种方法是使用MIMO雷达技术合成的非均匀或稀疏线性阵列(SLAs)[44-49]。在这种情况下，选择阵列元素的位置和利用虚拟稀疏阵列进行测角是关键问题。

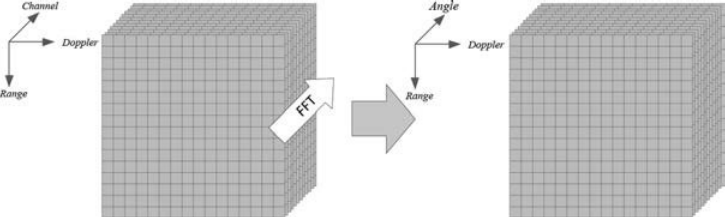
图3.6 数字波束形成(DBF)[6]

3.3.1 用ULA高分辨测角

3.3.1.1 具有空间平滑的子空间方法

?????? 基于子空间的寻角方法需要对阵列协方差矩阵进行估计。这样的估计通常是基于多个快照获得的。然而，在高度动态的汽车环境中，不可能在(3.16)模型变化之前获得足够的快照。在这种情况下，空间平滑[42]可以引入虚拟快照用于阵列协方差矩阵估计。在空间平滑中，阵列快照y被分成长度为L的重叠子阵列，以及一个新的采样阵列协方差矩阵是根据子阵列快照获取的。

????????R的特征值分解与Akaike信息标准度量[50]或最小描述长度度量[51]可以用来识别目标的数量。然而，应该指出的是，在这些标准的推导中，许多理想的假设，包括与源信号不相关的加性高斯白噪声，以及用于准确协方差矩阵估计的足够快照的可用性，在实践中可能无法得到满足。为此，在基于子空间方法的角度估计中，前向向后空间平滑技术[52]被广泛应用于估计子阵列协方差矩阵。子阵长度越短，可用于协方差矩阵计算的子阵越多，子空间估计越准确。然而，当子阵列长度较短时，DOA估计分辨率降低，因此需要在获取子阵列数量和子阵列长度之间进行权衡[53]。

通过识别MUSIC伪谱[26] 的峰的位置可以找到目标角度，在所有可能的θi处计算，即

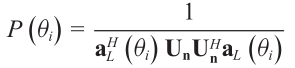??(3.7)

????????其中，Un是R的噪声子空间，是对应于搜索方向θi长度为L的阵列导向矢量。MUSIC算法由于存在角度搜索过程，计算量较大。也可以使用ESPRIT算法进行角度估计[27]。ESPRIT也是一种利用阵列位移不变性的子空间方法，在实践中得到了广泛的应用。它的复杂性比MUSIC低，但这是以降低角度分辨率为代价的。ESPRIT需要2L传感器。为了达到与MUSIC相同的角度分辨率，ESPRIT需要的传感器数量是MUSIC的两倍。由于汽车雷达需要二维阵列来估计方位角和仰角，如果阵列元素间距为均匀矩形，则可以采用二维ESPRIT算法[30]。

3.3.1.2 压缩感知

????????MIMO雷达配备了毫米波技术，提供宽带宽，从而实现高距离分辨率。因此，在同一距离-多普勒频域内的目标数量很少，目标在DOA空间上是稀疏的。基于稀疏感知的高分辨率目标角估计方法可以利用这一特性。将压缩感知(CS)应用于DOA估计，将整个DOA视场离散成一个精细网格。假设DOA空间离散在一个有N个点的网格上，网格上有K个目标。(3.16)中的数组响应可以重写为

????????y = Ax + n? (3.8)

????????其中A = [a (θ1),…,a (θN)]为基矩阵，其中a(θi)表示第i个网格点对应的阵列导向矢量，是一个有K个非零元素的稀疏向量。如果在第i个网格点上有目标，则βi的值为非零。基矩阵的相干性，定义为

??????????(3.9)

????????为获得统一的恢复保证，（相干性）需要小[54]。当满足所需的相干条件时，可以通过求解一个L1范数优化问题来求DOA，如定义如下的Dantzig选择器[55]:

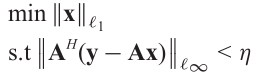??????????(3.10)

????????或贪心方法，如正交匹配追踪(OMP)[56]。

????????在上述公式中，假设目标在网格上，这在实践中并不总是可行的。虽然可以使网格更精细以捕获目标，但矩阵A的相干性会增加，这将使L1范数解无效[57]。因此，基于CS的方法的性能对网格中出现的目标很敏感[58]。稀疏感知和基于矩阵补全的方法[38,39]可以在不牺牲高分辨率性能的情况下避免网格问题。

3.3.1.3 迭代自适应方法

????????M元阵列快照yl，l=1,…,M的协方差矩阵可写为，其中P为K*K的对角矩阵，其对角元素包含目标反射的幂。(IAA)算法中的测角[40,41]是通过迭代估计反射系数βk来实现的，该估计是通过最小化加权最小二乘代价函数来找到的

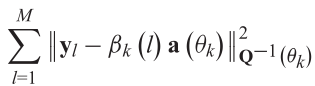??????????(3.11)

????????其中，干扰和噪声协方差矩阵。解由[40]给出

??????????(3.12)

????????矩阵P更新为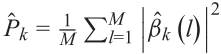。在IAA算法实现中，将DOA空间离散为N个点的精细网格，并以与CS相同的方式构造导向矩阵A。此外，使用标准延迟和波束形成器初始化P，

??????????(3.13)

3.3.2 稀疏线性阵列高分辨测角

????????如前所述，合成具有半波长单元间距的D元的大型虚拟ULA的成本非常高。在不牺牲高角分辨率的情况下进一步降低成本的一种方法是使用非均匀或SLA[44,45,59]。利用MIMO雷达技术，可以合成MtMr < D个虚拟阵元。为了使SLA孔径与ULA相同，需要在ULA边缘位置部署两个虚拟阵列阵元。对于剩余的虚拟数组元素，有多种部署的可能性。SLA的主要问题是栅瓣可能在测角中引入模糊。

????????在具有虚拟SLA的汽车MIMO雷达中，如果可以通过插值或外推技术填充虚拟SLA中的开口以减轻栅瓣，则仍然可以使用传统的FFT或ESPRIT方法进行角度查找[60,61]。

????????为了缓解稀疏阵列带来的高副瓣，我们利用矩阵补全技术对稀疏阵列中的开口进行内插/外推。此外，由于完全恢复的阵列中没有损耗/开口，因此矩阵补全提高了阵列响应的信噪比。

????????在典型汽车雷达场景的一次CPI中，可以在距离-多普勒频谱中检测到具有大量目标的密集点云[62]。在不规则的一维或二维稀疏数组中成功应用矩阵补全依赖于以下两个事实:

????????1.由于目标首先在距离多普勒域中分离，因此在同一距离多普勒域中需要进行角度估计的目标数量很少。换句话说，目标稀疏地存在于角度域中，因此，使用阵列响应构造的Hankel矩阵是低秩的。

????????2. 阵列快照中的信噪比远高于回波信号中的信噪比，因为能量已经通过IDFT和DFT操作在距离域和多普勒域积累。阵列快照的高信噪比有助于减小矩阵补全误差，提高角度估计的精度。

????????我们将通过一维稀疏阵列中的矩阵补全来说明阵列插值的概念，然后将其扩展到二维稀疏数组中。

3.3.2.1 通过矩阵补全的一维稀疏阵列插值

????????图3.7显示了一个汽车雷达的物理阵列配置示例，该雷达由两个MIMO收发器级联，其中所有发射和接收天线都是时钟同步的。设λ表示载波频率的波长。在本例中，Mt = 6个发射天线和Mr = 8个接收天线沿方位角方向在离散网格点上部署，间隔长度为50λ。间隔以半波长间隔均匀离散。来自每个发射天线的波形以一种方式发射，在每个接收天线，每个发射天线的贡献可以通过DDM分离。因此，利用MIMO雷达技术，合成了一个48个阵元、孔径75λ的虚拟SLA，如图3.7所示。与具有半波长元间距和相同孔径的ULA相比，在渲染的虚拟SLA中，某些位置的大量阵元“缺失”(图3.7虚拟阵列中以零表示)。然而，SLA方法仅使用Mt + Mr = 14个物理天线，显著降低了相互耦合效应[6]。

????????假设一个阵列快照包含K个DOAs为θk的目标，k= 1,…,K。在不加噪声的情况下，SLA响应可以表示为

??????????(3.14)

图3.7 级联两个收发器的汽车雷达示例。虚拟阵列有48个阵元。[5]

????????其中是集合矩阵，且

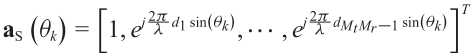??????????(3.15)

????????di是SLA的第i个阵元和参考阵元之间的距离。另外，，其中βk表示和第k个目标关联的幅度。

????????考虑一个虚拟的ULA，它跨越整个阵列孔径，并且充满了间隔为阵元间距d = λ/2的天线。该虚拟ULA中的天线总数为Mo，无噪声阵列响应表示为

??????????(3.16)

????????其中，是集合矩阵，且

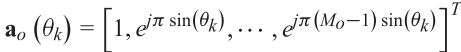??????????(3.17)

????????令N2=M0/2，且N1=M0-N2≥N2。我们可以把表示成N2个长度为N1的重叠子阵。基于这些子阵，我们用它的第(i,j)个阵元给定的表示Hankel矩阵，i=1,…,N1、j=1,…,N2。Hankel矩阵Y具有范德蒙德分解[63]，表示为

??????????（3.18）

????????其中是子阵集合矩阵，且

??????????(3.19)

????????是一个对角矩阵。因此，如果N2≥K，Hankel矩阵Y的秩是K。

????????我们可以类似地从SLA配置构造一个Hankel矩阵X。然而，与由完整ULA构造的矩阵Y不同，矩阵X有许多缺失条目，因此可以将其视为Y的次采样版本。在一定条件下，通过求解以观测项为条件的松弛核范数优化问题，可以完全恢复缺失的元素[64]

??????????(3.20)

????????式中||.||*为矩阵的核范数，为采样算子，Ω为由SLA确定的观测项的指标集合。实际上，样本被噪声破坏，即[X]ij=[Y]ij+[E]ij，(i,j)∈Ω，其中[E]ij表示噪声。在这种情况下，矩阵补全问题表示为

??????????(3.21)

????????其中||.||F表示矩阵的Frobenius范数，而δ是由噪声功率决定的常数。

????????一旦矩阵Y恢复，则通过平均其反对角项来获得整个阵列响应。DoA可以根据完成矩阵Y对应的阵列响应，通过标准的阵列处理方法来估计。

????????为了获得高方位角分辨率，将多个车载雷达收发器级联在一起，在方位角上合成一个大的稀疏阵列。这里，我们考虑图3.7所示的相同物理阵列，其中Mt=6个发射天线和Mr=8个接收天线沿水平方向交错放置在

????????

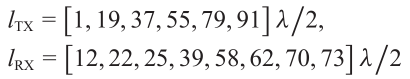
????????合成了一个共有48个元素的虚拟阵列。发射天线和接收天线以及虚拟阵列如图3.7所示。

????????两个目标在同一距离R = 100 m，速度v = 10 m/s。它们各自的方位角是θ1=0°和θ2=20°。两个目标首先在距离上被多普勒分离。每个虚拟稀疏阵列对应的距离多普勒频谱中的复峰值由阵列快照组成，用于方位角查找。

????????图3.7所示的虚拟SLA作为2级汉克尔矩阵( N=76)的确定性采样器，它是基于包含152个阵元的ULA的阵列响应构建的。

????????SLA的阵列响应由其第一个阵元归一化。基于观察到的SLA响应，通过奇异值阈值(SVT)算法完成Hankel矩阵Y[65]。设表示完成的Hankel矩阵。通过对矩阵的反对角线阵元取平均值，可以重构出全ULA响应，完成的全阵列孔径为76λ。直观地说，在这个仿真设置中，矩阵补全对阵列处理的信噪比提高了约10 log10(152/48)≈5dB。

????????在图3.8中，我们绘制了两个目标的角度谱。分别用FFT对原SLA进行填零开口处理和对全阵列进行矩阵补全处理得到两个方位角谱。研究发现，该算法的FFT以高副瓣为代价产生了两个对应于正确方位角方向的峰值，因此在原算法下很难检测到方位角方向上的两个目标。相反，完整的全阵在角谱中呈现出两个清晰的峰，对应于正确的方位角位置，并且副瓣在完整的全阵中得到了很大的抑制。

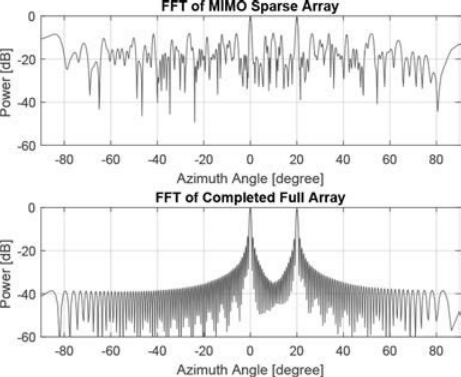
图3.8 方位角θ1=0°和θ2=20°的两个目标在MIMO稀疏阵列和完全补全阵列的频谱。[5]

3.3.2.2 通过矩阵补全的二维稀疏阵列插值

????????为了实现驾驶上穿和驾驶下穿功能，汽车雷达必须准确测量目标仰角。因此，汽车雷达需要在方位角和仰角方向上提供高角度分辨率的点云。图3.9显示了一个MIMO雷达，其中有12个发射天线和16个接收天线，由4个车载雷达收发器级联得到，发射天线和接收天线随机部署在[0,100] (λ/2)*[0,120] (λ/2)区域内，合成一个196个阵元的MIMO二维虚拟稀疏阵列。当载波频率为fc = 77GHz时，二维物理阵列对应的外形尺寸约为20*24 cm2。应该指出的是，在实践中应该考虑角分辨率和雷达外形尺寸之间的权衡，以便雷达可以并入汽车保险杠后面。渲染的二维虚拟稀疏阵列维数为D y * D x = 183(λ/2)*194(λ/2)，可以看作是在水平方向和垂直方向上具有半波长间隔的相同维数的均匀矩形阵列(URA)的空间亚奈奎斯特采样。方位角分辨率和仰角分辨率分别表示为[43]

??????????（3.22）

??????????? （3.23）

????????本例中成像雷达的角度分辨率与Velodyne LiDAR HDL- 32E相当，其水平分辨率根据旋转速率在0.1°到0.4°之间，垂直分辨率为1.33°[66]。

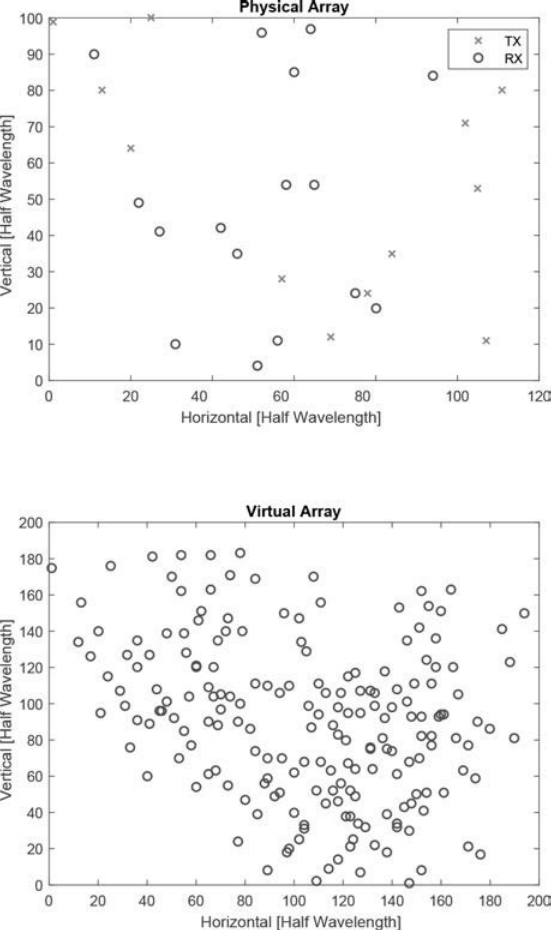
????????图3.9 级联4个汽车雷达收发器有12个发射天线和16个接收天线的MIMO雷达。发射天线和接收天线随机部署在[0,100] (λ/2)*[0,120] (λ/2)区域内，合成一个196个阵元的MIMO二维虚拟稀疏阵列。

????????考虑一个常规案例，M1*M2的URA间距半波长，如图10所示，这里URA在x-y平面。假设第k个点目标方位角θk，俯仰角φk。让χk表示第k个目标和x轴的夹角，?k表示第k个目标和y轴的夹角。因此，会有cos(χk)=sin(φk)cos(θk)，cos(?k)=sin(φk)sin(θk)。所以，

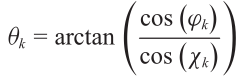??????????(3.24)

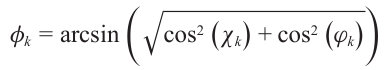??????????（3.25）

????????一旦χk和?k已知，方位角θk和俯仰角φk能被唯一确定。为了简化信号模型，在URA中使用χk和?k做信号建模。

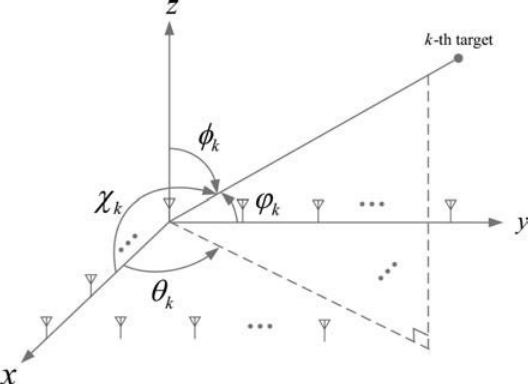
图3.10 常规URA的阵列示意图[5]

????????URA阵列在x-y平面上的第(m1,m2)个阵元对应于和x轴夹角为χk、y轴夹角为?k的K个目标的响应，k=1,…,K,可以写为

??????????（3.26）

????????其中1≤m1≤M1，1≤m2≤M2。设M=[xm1,m2] 0≤m1≤M1，0≤m2≤M2为数据矩阵，其条目为(3.26)中定义的URA阵列响应。我们可以构造一个N1*(M1-N1+1)块Hankel矩阵为

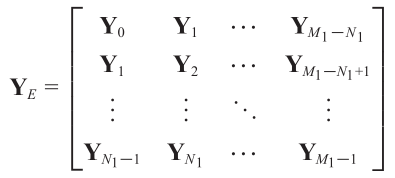??????????（3.27）

????????其中

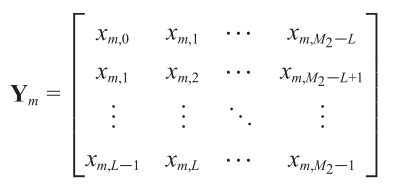??????????(3.28)

????????是一个L*(M2-L+1) Hankel矩阵。可以验证矩阵YE的秩为K，当N1≥K, L≥K[67]。

????????通过选择发射和接收天线的位置，我们的目标是合成一个稀疏的二维阵列，这可以看作是市建局的空间子采样。URA的阵列响应可以根据稀疏阵列的阵列响应完成块Hankel矩阵YE得到。块Hankel矩阵补全问题表示为

??????????(3.29)

????????式中，Ω为由二维稀疏虚拟阵列阵元位置组成的观测集，XE为由矩阵X根据式(3.27)和式(3.28)构造的块Hankel矩阵。在嘈杂的观测场景中，M由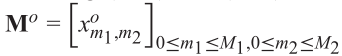代替，并且，这里表示观测信号，是噪声项。我们假设噪声是有界的，即。噪声块Hankel矩阵补全问题表示为

????????? (3.30)

????????以上优化问题可以在CVX工具箱中解决[68]。在仿真中，我们采用SVT算法[65]来解决矩阵补全问题，该算法每次迭代更新低秩矩阵的计算代价为m阶，m为观测集Ω的基数，即m =|Ω|。

????????通过级联汽车雷达收发器，我们考虑了图3.9所示的相同的二维物理阵列，用于联合高分辨率方位角和仰角估计。这12个发射天线和16个接收天线随机部署在一个[0,100] (λ/2)*[0,120] (λ/2)区域，合成一个196个单元的二维MIMO虚拟阵列。级联式汽车雷达外形尺寸约为20*24厘米。在图3.9中，二维稀疏阵列的维数为Dy* Dx = 183(λ /2) * 194(λ /2)。构建具有半波长间隔的相同维数的URA总共需要35,502个阵元。也就是说，虚拟稀疏阵列只占URA总阵元的0.54%。

????????考虑具有相同距离和多普勒bin的两个目标。它们与x和y方向的夹角分别是(χ1,?1)=(-20°,5°)，(χ2,?2)=(20°,10°)。稀疏阵列快照由每个稀疏阵列元素对应的距离-多普勒频谱中的复峰值组成。阵列响应的输入信噪比设置为20 dB，这在汽车雷达中是合理的，因为快时间和慢时间相干处理提供了较高的处理增益。然后，我们使用这个包含196个元素的二维稀疏阵列的一个阵列快照来构造一个维数为9,009 *8,928的块Hankel矩阵YE。只有0.78%的Hankel矩阵条目是非零的。基于二维稀疏阵列的一个快照，通过SVT算法完成块Hankel矩阵，得到完整的URA。在这个仿真设置中，矩阵补全为阵列处理贡献了大约10 log10(35502/196)≈ 22.5 dB信噪比增益。

????????图3.11和图3.12分别绘制了两个目标在二维稀疏阵列和完成的全URA下的方位角-仰角频谱。研究发现，稀疏阵列和URA都会产生两个峰值，对应目标的正确方位角和仰角。然而，在二维稀疏阵列的方位角-俯仰角谱中，整个方位角和仰角视场都存在高副瓣。相反，在已建成的URA内，高旁瓣会得到缓解。

?????? 图3.11 目标方位角和俯仰角为(χ1,?1)=(-20°,5°)，(χ2,?2)=(20°,10°)的两个目标在稀疏阵列下的频谱。目标的角度用十字标记。由于稀疏阵列中存在大量的缺口，频谱中存在较高的副瓣。[5]

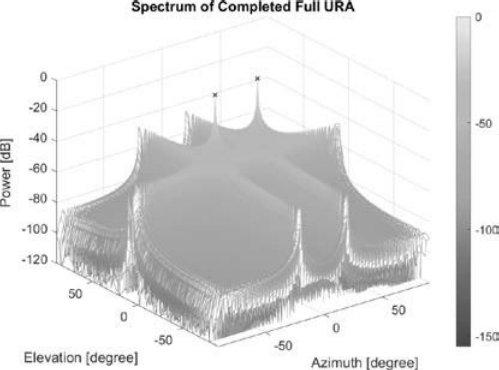
?????? 图3.12 目标方位角和俯仰角为(χ1,?1)=(-20°,5°)，(χ2,?2)=(20°,10°)的两个目标在补全的URA下的频谱。目标的角度用十字标记。[5]

3.3.2.3 SLA优化

????????或者，可以使用空间压缩感知(CS)思想对稀疏阵列进行测角，而不是填充缺口[69]。在这种情况下，关键问题是如何选择阵列元素的位置，使虚拟SLA波束方向图的峰值旁瓣电平(PSL)较低，以及如何进行测角。对于给定数量的天线，没有解析解来确定达到最小PSL的天线位置[70]。最优稀疏阵列设计需要全局优化技术，如粒子群优化[45,71,72]。

????????在SLA场景中，可以很容易地验证基矩阵的相干性(见3.9)是SLA阵列波束方向图的PSL[44]。因此，稀疏阵列的相干性或等效的PSL对于CS的均匀恢复保证起着关键作用[54]。如果SLA的PSL较低，则可以通过CS或IAA使用SLA进行角度查找。

????????在图3.13中，我们给出了一个孔径为19λ的虚拟SLA示例，该示例采用MIMO雷达技术合成，使用四个发射四个接收天线。第一和第四个发射/接收天线部署在物理孔径的边缘，而其余天线的选择使得PSL为-9.1dB。使用图3.13的SLA时通过IAA进行的角度估计如图3.14所示。地面真值涉及两个方位角为5°和10°的目标。接收波束矢量的信噪比设为30dB。为了比较，还绘制了FFT谱。与FFT频谱相比，可以在IAA频谱中观察到目标方位角周围更尖锐的峰值和更衰减的副瓣。

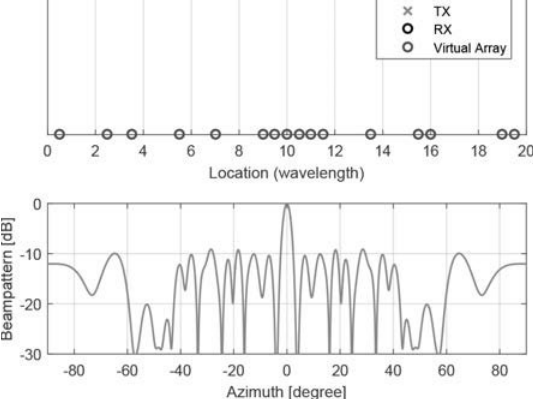
????????图3.13 采用MIMO雷达技术合成的SLA仿真示例，采用四个发射和四个接收天线。阵列孔径的物理极限为10λ。我们将第一和第四发射/接收天线的位置分别设置为0λ, 0.5λ和10λ, 9.5λ，这样可以实现最大虚拟阵列孔径为19λ。选择剩余的发射/接收天线，使合成虚拟阵列波束方向图的PSL为?9.1 dB。[6]

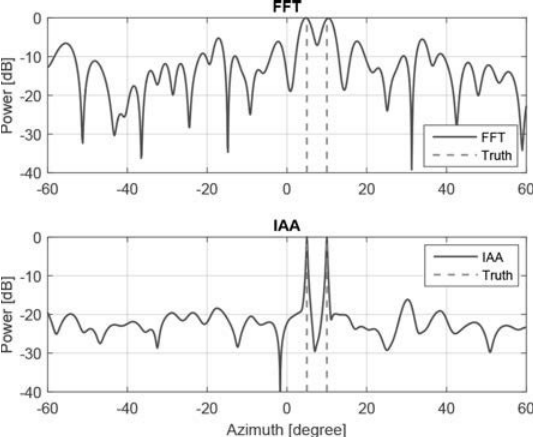
????????图3.14 通过IAA方法测角和使用图3.13所示SLA的FFT频谱，由MIMO雷达技术合成。有两个目标，方位角分别为5°和10°。信噪比设置为30dB。[6]