北京交通大学高性能作业——CPU SIMD + GPU SIMD

1. CPU SIMD

Intel SIMD

运行代码和截图

#include <stdio.h>
#include <xmmintrin.h> // Need this for SSE compiler intrinsics
#include <math.h> // Needed for sqrt in CPU-only version
#include <time.h>

int main(int argc, char* argv[])
{
    printf("Starting calculation...\n");
    const int length = 64000;

    // We will be calculating Y = SQRT(x) / x, for x = 1->64000
    // If you do not properly align your data for SSE instructions, you may take a huge performance hit.
    float *pResult = (float*) _aligned_malloc(length * sizeof(float), 16); // align to 16-byte for SSE
    __m128 x;
    __m128 xDelta = _mm_set1_ps(4.0f); // Set the xDelta to (4,4,4,4)
    __m128 *pResultSSE = (__m128*) pResult;

    const int SSELength = length / 4;
    clock_t clock1=clock();
    #define TIME_SSE // Define this if you want to run with SSE
    #ifdef TIME_SSE
    // lots of stress loops so we can easily use a stopwatch
    for (int stress = 0; stress < 1000; stress++)
    {
        // Set the initial values of x to (4,3,2,1)
        x = _mm_set_ps(4.0f, 3.0f, 2.0f, 1.0f);
        for (int i=0; i < SSELength; i++)
        {
            __m128 xSqrt = _mm_sqrt_ps(x);
            // Note! Division is slow. It's actually faster to take the reciprocal of a number and multiply
            // Also note that Division is more accurate than taking the reciprocal and multiplying

            #define USE_DIVISION_METHOD
            #ifdef USE_FAST_METHOD
            __m128 xRecip = _mm_rcp_ps(x);
            pResultSSE[i] = _mm_mul_ps(xRecip, xSqrt);
            #endif //USE_FAST_METHOD
            #ifdef USE_DIVISION_METHOD
            pResultSSE[i] = _mm_div_ps(xSqrt, x);
            #endif // USE_DIVISION_METHOD
            // Advance x to the next set of numbers
            x = _mm_add_ps(x, xDelta);
        }
    }
    clock_t clock2=clock();
    printf("SIMDtime:%d ms\n",1000*(clock2-clock1)/CLOCKS_PER_SEC);
    #endif // TIME_SSE

    #define TIME_NoSSE
    #ifdef TIME_NoSSE
    clock_t clock3=clock();
    // lots of stress loops so we can easily use a stopwatch
    for (int stress = 0; stress < 1000; stress++)
    {
        clock_t clock3=clock();
        float xFloat = 1.0f;
        for (int i=0 ; i < length; i++)
        {
            // Even though division is slow, there are no intrinsic functions like there are in SSE
            pResult[i] = sqrt(xFloat) / xFloat;
            xFloat += 1.0f;
        }
    }
    clock_t clock4=clock();
    printf("noSIMDtime:%d ms\n",1000*(clock4-clock3)/CLOCKS_PER_SEC);
    #endif // TIME_noSSE
    return 0;
}

图1-1 PC上的CPU SIMD性能比较

结果分析

这段程序比较了SIMD使用SSE指令集和不使用SIMD两种方式的计算速度差距，程序计算的是√x/x，发现SIMD使用SSE指令集可以并行四个浮点数进行计算，结果确实会比不使用SIMD更快。

---

Kunpeng SIMD (ARM NENO)

运行代码与截图

#include <stdio.h>
#include "arm_neon.h"

void add3 (uint8x16_t *data){
    uint8x16_t three = vmovq_n_u8(3.0);
    *data = vaddq_u8(*data, three);
}

void print_uint8(uint8x16_t data, char* name){
    int i;
    static uint8_t p[16];
    vst1q_u8(p,data);
    printf("%s = ",name);
    for (i =0 ; i<16; i++){
        printf("%02d",p[i]);
    }
    printf("\n");
}

int main(){
const uint8_t uint8_data[] ={1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0,11.0,12.0,13.0,14.0,15.0,16.0};
    uint8x16_t data;
    data = vld1q_u8(uint8_data);
    print_uint8(data, "data");
    add3(&data);
    print_uint8(data,"data (new)");
    return 0;
}

图1-2 TaiShan服务器运行ARM NENO文件

结果分析

程序使用了ARM NEON指令集提供的函数实现了对16个uint8_t类型的数据进行并行计算。add3函数是使16个unit8_t元素的向量每个元素加3。其中vmovq_n_u8函数创建了一个有16个uint8_t 类型元素的向量three，每个元素值都是3。vaddq_u8函数将three和data中每个对应元素相加，将结果写回data。print_uint8函数，用于打印uint8x16_t类型的向量，方法是先把向量元素的值存储到数组再打印。主函数中定义了一个uint8_data数组，包含了16个 uint8_t类型的数据再转化为16个元素的向量data。print_uint8函数打印出data最初的值，再调用add3函数操作data，最后调用print_uint8函数打印出计算后的值。

---

2.GPU SIMD

CUDA installation information

通过win + r输入cmd打开命令行，用nvcc -V查看cuda的安装信息，我安装的版本是11.6

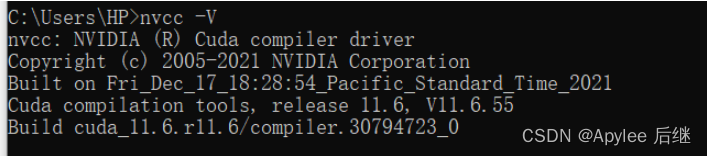
图2-1-1 CUDA installation information

---

deviceQuery in CUDA

进入我安装CUDA的位置，并运行deviceQuery，可以看到给出了详细的设备信息，里面有我的显卡型号和最大的计算能力，以及运行内存和主频等。

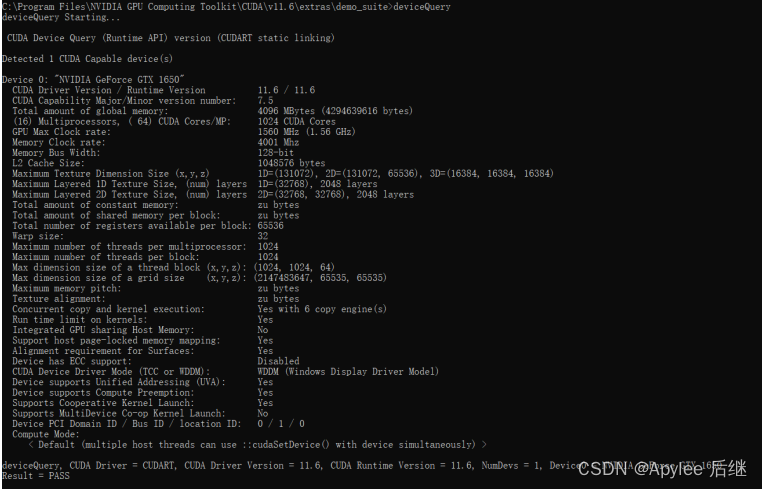
图2-2-1deviceQuery in CUDA

---

Vector calculation in CUDA

运行代码及截图

#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <cuda.h>

// Kernel that executes on the CUDA device
__global__ void square_array(float* a, int N)
{
	int idx = blockIdx.x * blockDim.x + threadIdx.x;
	if (idx < N) a[idx] = a[idx] * a[idx];
}

int main()
{
	float* a_h, * a_d;  // Pointer to host & device arrays
	const int N = 10;  // Number of elements in arrays
	size_t size = N * sizeof(float);
	a_h = (float*)malloc(size);        // Allocate array on host
	cudaMalloc((void**)&a_d, size);   // Allocate array on device
	// Initialize host array and copy it to CUDA device
	for (int i = 0; i < N; i++) a_h[i] = (float)i;
	cudaMemcpy(a_d, a_h, size, cudaMemcpyHostToDevice);
	// Do calculation on device:
	int block_size = 32;
	int n_blocks = N / block_size + (N % block_size == 0 ? 0 : 1);
	square_array << < n_blocks, block_size >> > (a_d, N);
	// Retrieve result from device and store it in host array
	cudaMemcpy(a_h, a_d, sizeof(float) * N, cudaMemcpyDeviceToHost);
	// Print results
	for (int i = 0; i < N; i++) printf("%d %f\n", i, a_h[i]);
	// Cleanup
	free(a_h); cudaFree(a_d);
	return 0;
}

图2-3-1 Vector calculation in CUDA

结果分析

程序创建了一个包含10个元素的浮点数数组。把数组从主机内存复制到显卡的内存中。计算了该数组每个元素的平方，并将结果存到显卡的内存中。最后，它从显卡内存中将计算结果复制回主机内存，打印出内阁元素的索引以及对应的平方值。计算过程采用了并行计算，这里设置了每个线程块包含32个线程，每个线程计算一个数组元素的平方。由于数组大小为10，因此只需要启动1个线程块

---

PI calculation in CUDA

运行代码及截图

#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <cuda.h>
#include <math.h>
#include <tchar.h>
#include <time.h>
#define NUM_THREAD 1024
#define NUM_BLOCK 1

__global__ void cal_pi(double* sum, long long nbin, float step, long long nthreads, long long nblocks) {

	long long i;
	float x;
	long long idx = blockIdx.x * blockDim.x + threadIdx.x;

	for (i = idx; i < nbin; i += nthreads * nblocks) {
		x = (i + 0.5) * step;
		sum[idx] = sum[idx] + 4.0 / (1. + x * x);
	}

}

int _tmain(int argc, _TCHAR* argv[])
{
	long long tid;
	double pi = 0;
	long long num_steps = 100000000;

	float step = 1. / (float)num_steps;
	long long size = NUM_THREAD * NUM_BLOCK * sizeof(double);
	clock_t before, after;
	double* sumHost, * sumDev;
	sumHost = (double*)malloc(size);
	cudaMalloc((void**)&sumDev, size);
	// Initialize array in device to 0
	cudaMemset(sumDev, 0, size);
	before = clock();
	// Do calculation on device
	printf("Before Compute \n\n");
	dim3 numBlocks(NUM_BLOCK, 1, 1);
	dim3 threadsPerBlock(NUM_THREAD, 1, 1);
	cal_pi << <numBlocks, threadsPerBlock >> > (sumDev, (int)num_steps, step, NUM_THREAD, NUM_BLOCK); // call CUDA kernel

	printf("After Compute \n\n");
	// Retrieve result from device and store it in host array
	cudaMemcpy(sumHost, sumDev, size, cudaMemcpyDeviceToHost);
	printf("After Copy \n\n");
	for (tid = 0; tid < NUM_THREAD * NUM_BLOCK; tid++) {
		pi = pi + sumHost[tid];
	}
	pi = pi * step;
	after = clock();
	printf("The value of PI is %15.12f\n", pi);
	printf("The time to calculate PI was %f seconds\n", ((float)(after - before) / 1000.0));
	free(sumHost);
	cudaFree(sumDev);
	return 0;
}

图2-4-1 只调用1个线程块算出pi所花费的时间

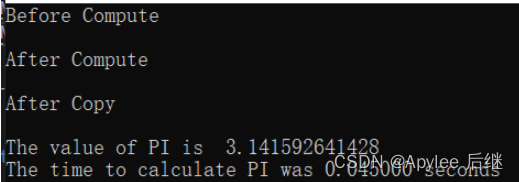
图2-4-2 根据显卡的线程块上限调整代码后，速度快了十倍之多

结果分析

使用CUDA计算圆周率的程序。程序中sumHost和sumDev两个数组分别在主机和显卡内存中存储计算结果，cudaMalloc函数和cudaMemset函数在显卡开辟空间以及清零，然后执行cal_pi函数对圆周率进行计算。计算是在显卡上并行地运行的，它会根据输入的参数计算圆周率，并将结果存储在传入的sum数组中。每个线程计算一部分区域的和，即计算左端点为 (i+0.5)*step，右端点为 (i+1.5)*step 的小矩形面积，并加到sum[idx]中，最后程序输出圆周率的值以及所花费的时间。计算前用numBlocks和threadPerBlock来分别指定线程块数量和线程数。用<<<numBlocks,threadsPerBlock>>>来指定使用多少个线程块和每个线程块中包含多少个线程。