实时渲染 -- 着色（Shading)

着色是一个很重要的环节，它负责计算出颜色（光栅化只是填充像素格，换句话说是负责转移颜色到屏幕），着色计算要考虑的因素通常有：光照、纹理、着色频率（着色单位）等。

当然，现在着色的概念已经扩张到不是单纯的输出颜色，有时还可能需要输出别的属性（例如顶点着色器vertex shader可以输出修改后的顶点属性）。

Blinn-Phong 光照模型

光的能量基本规律

朗伯余弦定律认为，当光源照射方向与表面法线夹角越小，物体表面接受的光的能量就会越多：

?其次，能量也存在衰减现象，其能量和与光源距离的平方成反比：

能量时刻向外扩散，因此随着距离的平方越大，球表面面积也越大，每单位面积能量强度便越小

?

现实世界的光是非常复杂，这些基本规律其实还远远不够，而前人基于这些简单原理，就提出了Blinn-Phong 光照模型。

Blinn-Phong 是一个经典的经验光照模型（非现实物理）,它使用三种类型的光叠加而成得到光照结果。

?环境光（Ambient)

现实世界存在大量间接光照（即多次反射后最终经过目标物体并最终反射到眼睛的光），但是计算这些间接光照过于复杂，Blinn-Phong模型直接将这类间接光的总和表示为环境光??，并且每个着色材质以一个系数?来控制其接受环境光的程度。

漫反射光（Diffuse）

漫反射光则是常见的一种物理现象（粗糙的表面会将入射光均匀反射），因此漫反射光只通过计算入射光线与着色表面法线的点乘（朗伯余弦定律），并用max函数避免夹角为负数（0意味着摄像机看不到着色点），然后乘上光的能量（能量衰减后的），最后同理每个着色材质以一个系数 ?来控制其接受漫反射光的程度。

高光（Specular）

高光则基于镜面反射现象（当眼睛观测方向与光反射方向相向时会看到最亮的颜色），也就是说眼睛观测方向?v?与反射方向?R?夹角越接近，则接受的光能量也越多：

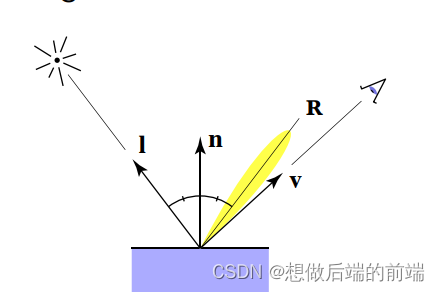
而Blinn-Phong假设，一个半程向量（观测方向v和入射方向l的中间方向）与表面法线的角度α，近似等于观测方向v?与反射方向?R?的夹角（因为V接近R等价于h接近n，而且偏差也可以通过系数调整）。使用半程向量计算夹角的好处是相比后者计算量大大减少。使用p次方是为了体现高光特性（亮者更亮，暗者更暗，从而突出亮光），最后同理每个着色材质以一个系数??来控制其接受高光的程度。

半程向量：?

Blinn-Phong 光照总结

BlinnPhong（光照结果） =?Ambien（环境光）+?Diffuse（漫反射光） +?Specular（高光）

这样我们可以通过以下三个参数来表示一个着色物体的材质:

• ?调整一个着色材质的基础光照影响程度
• 调整一个着色材质的漫反射接受程度
• ?调整一个着色材质的高光接受程度

光源模型?

除了光照模型，我们还应该提供光源模型以供模拟完整的光照场景；假设我们当前有1个物体，n?个光源，在对该物体每个像素点着色（主要指前向渲染）的时候，我们需要进行?O(n)?次光照计算（根据每个光源模型特性计算一次）。

环境光（Ambient Light）

影响因素：强度、颜色

这种类型的光源来自空间中的任何地方，并以相同的方式照亮所有物体，可以理解成所有物体的基础光照颜色。

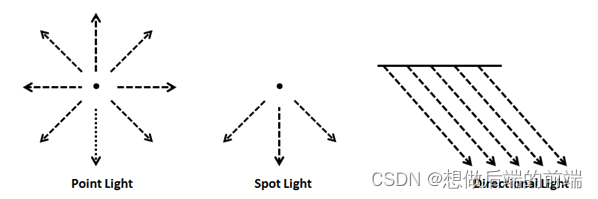
点光源（Point Light）

影响因素：强度、颜色、位置、衰减系数

点光源是从一个具体的点位置向外散发光线。

聚光灯（Spot Light）

影响因素：强度、颜色、位置、衰减系数、方向、夹角

聚光灯就是在点光源的基础之上加上了方向和夹角的概念，使其只在某些方向向外散发光线

方向光（Directional Light）

影响因素：颜色、方向、强度

可以理解成无数个平行光照射过来（类似太阳照射地面上的物体），无论在哪个地方收到的入射光方向都是一样的。

着色频率（着色单位）

给物体着色的一个问题是：我们该给物体每个面进行一次着色还是每个点进行一次着色。容易知道，着色频率越高，其效果更真实，但是代价也就越高。

基于面的着色（Flat shading）

对每个三角面进行一次着色计算，因此根据光照模型的着色得到的结果将会是同个三角面都是同一颜色：

计算三角形法线：简单地将两条边叉乘得出三角形的法线，并且还需要进行标准化

基于顶点的着色（Gouraud shading）

对每个顶点进行一次着色计算，然后三角形内部像素点则通过在三角形的重心坐标插值（Barycentric Interpolation）得到颜色：

计算顶点近似法线：简单地将与顶点衔接的面法线平均起来。

基于像素的着色（Phong shading）

基于像素的着色是实际上最常用的着色频率，它对每个像素点进行一次着色计算，得到更加真实的效果：

计算像素近似法线：三角形内部像素点通过在三角形的重心坐标插值得到向量，最后这个插值出来的向量还需要标准化：

在现在的渲染管线中，往往提供了可编程的vertex shader和pixel/fragment shader来让开发者决定顶点着色器和像素着色器分别进行什么着色计算。由于现代GPU性能的强大，我们都习惯在pixel/fragment shader进行光照计算以获得更好的视觉效果。