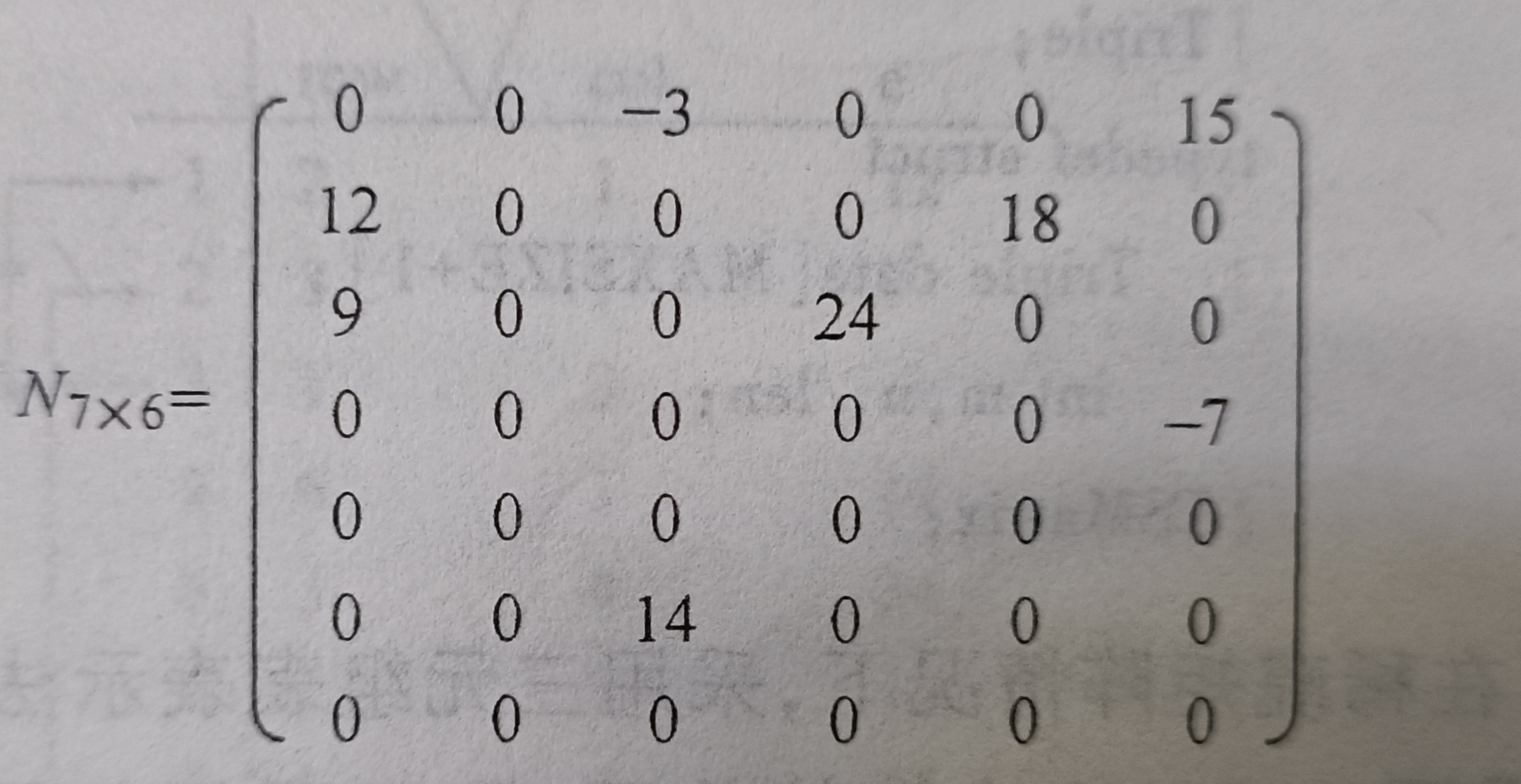【数据结构】特殊矩阵的压缩存储|保姆级详解+图解

• 作者：努力学习的大一在校计算机专业学生，热爱学习和创作。目前在学习和分享：算法、数据结构、Java等相关知识。
• 博主主页： @是瑶瑶子啦
• 所属专栏: 【数据结构】：该专栏专注于数据结构知识，持续更新，每一篇内容优质，浅显易懂，不失深度！
• 近期目标：写好专栏的每一篇文章

📌一、特殊矩阵的压缩存储

📍1.1：前言

在线性代数这门学科中已经学习了矩阵。在高级计算机语言中，矩阵常用二维数组表示。
所谓**“压缩存储”**，目的在于节省空间！体现在，为多个值相同的元素只分配一个存储空间，多元素值为0的元素不分配空间

• 二维数组A[n][n]和A[0...n-1][0...n-1]的写法是等价的。如果数组写法为A[1..n]A[1..n],则说明指定了下标是从1开始存储元素。二维数组元素写为a[i][j],注意数组元素下标i和j通常是从0开始的。矩阵元素通常写为a i,j或者a(i),(j)，注意这时的i和j代表的行号和列号，都是从1开始的！

这里我们讨论两种特殊矩阵

1. 元素分布有特殊规律的矩阵，寻找规律对应的公式实现压缩存储
   • 三角矩阵（上三角、下三角、对称矩阵）
   • 带状矩阵
2. 稀疏矩阵
   • 三元组表示法
   • 十字链表

📍1.2：规律矩阵

💥这里给出实现压缩（矩阵元素A(i)(j)在压缩后一维数组B[]中的下标对应关系）的核心公式：

• 矩阵非零元素A(i)(j)在一维数组B中求对应下标

$$Loc[i,j]=Loc[1,1]+(a(i)(j)前面的非零元素个数））$$

• 矩阵非零元素a(i)(j)在一维数组B中地址(size是单个元素的字节大小）

$$Loc[A(i)(j)]=Loc[A(1,1)]+(a(i)(j)前面的非零元素个数))?size$$

由于通常Loc[1,1]即A(1)(1)在一维数组B中下标是0（下面给的公式也是按照B数组下标从0开始），所以0就被省略，没有写出来

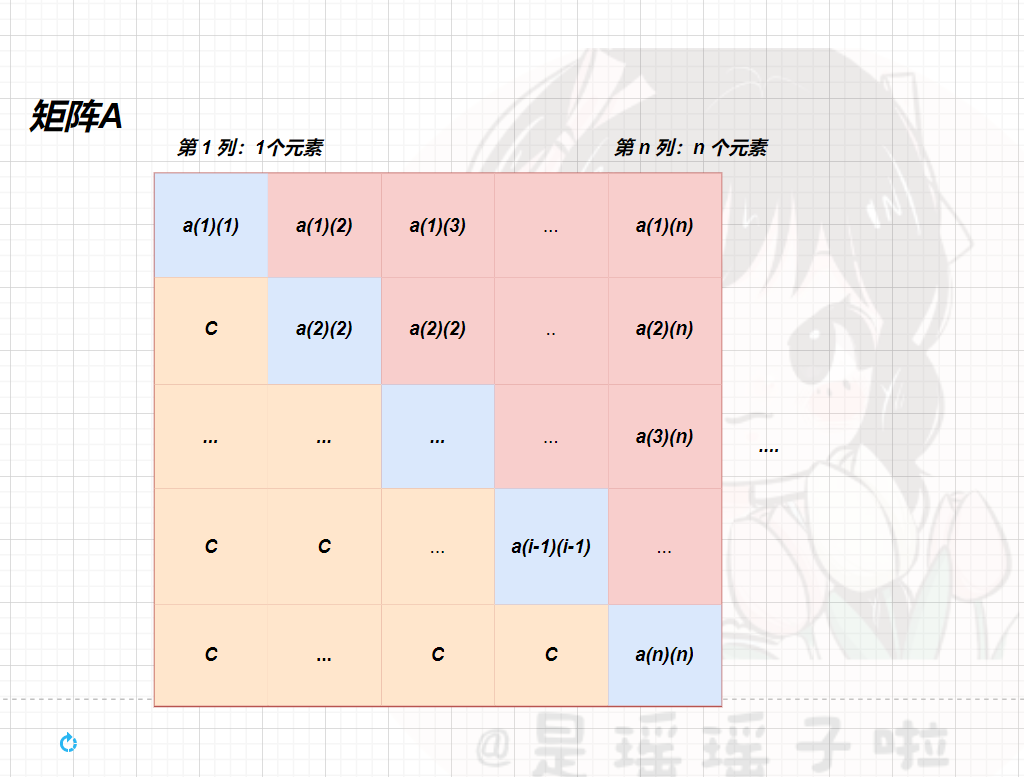
1.2.1：三角矩阵

🍊对于一个n阶矩阵A来说：

• 对称矩阵

  • 矩阵中所有元素都满足a(i)(j) = a(j)(i)

• 下三角矩阵

  • i < j时（在对角线之上），有a(i)(j) = c (当 c = 0，时，上三角区域元素均为0）

• 上三角矩阵

  • i > j时（在对角线之下），有a(i)(j) = c (当 c = 0，时，下三角区域元素均为0）

📪1.2.1.1：对称矩阵

对于对称矩阵，我们知道在下三角区域和上三角区域存在a(i)(j) = a(j)(i)，我们其实只用存储下三角（或者上三角）+ 对角线这部分区域的元素即可，节省了上三角区域元素所占用空间。

所以，我们可以将一个n阶的对称矩阵A，存储在一个一维数组B[(n + 1)*n /2]中（下面以下三角矩阵存储为例，注意，一维数组B的下标设为从0开始！）

那么我们只用知道元素a(i)(j)元素在B数组中的下标，即可实现压缩！而a(i)(j)在B数组中的下标和其i和j有关（类似于把二维数组中元素按行优先或者按列优先，转存到一维数组中！）

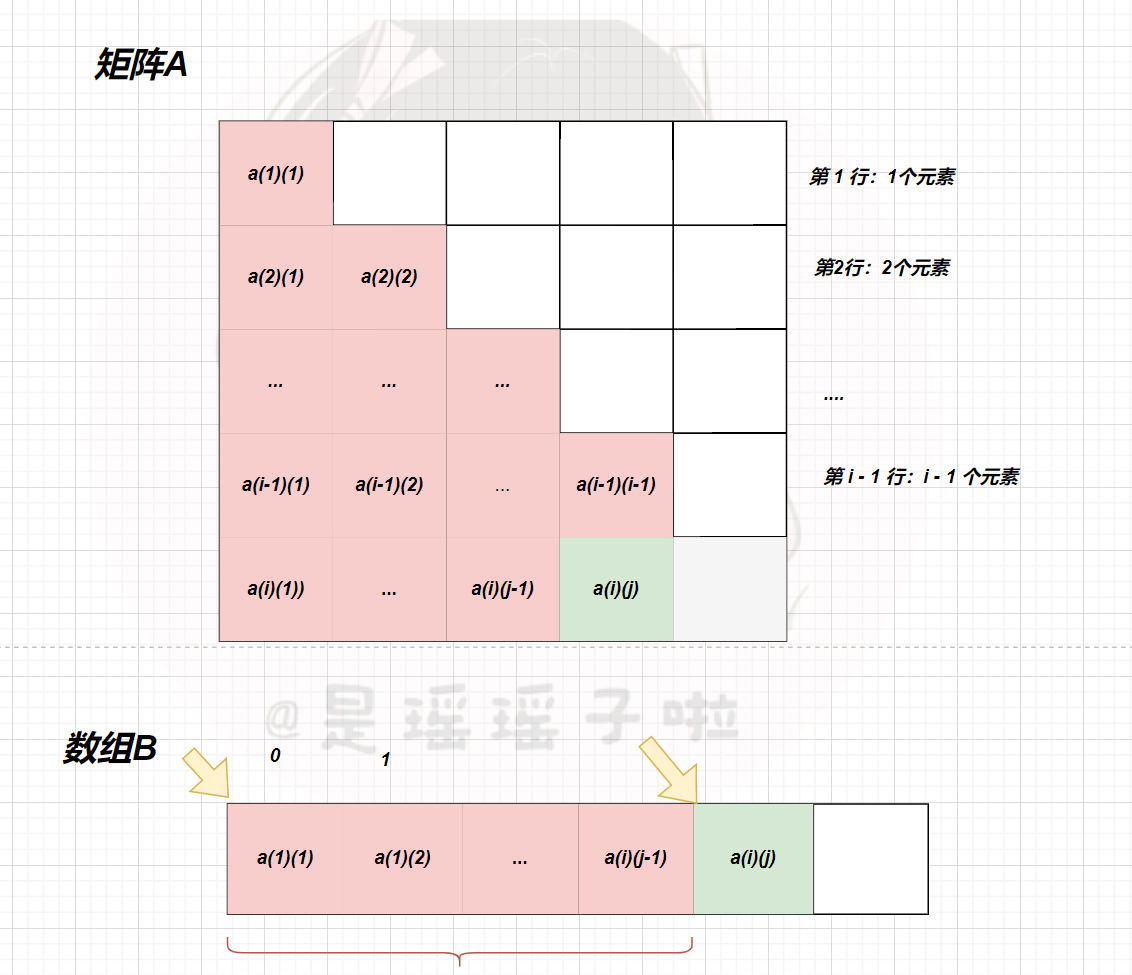
🌳压缩核心：求出a(i)(j)前面有多少个元素，0 + 相差元素个数（指针跳过中间相差元素个数），得到的就是a(i)(j)在B数组中的下标（其实也是地址的映射）
🥕公式 |a(i)(j)在B数组中的下标K：

• i >= j,下三角区域和主对角线元素

$$k=\frac{i(i?1)}{2}+j?1$$

• 对于上三角区域，由于a(i)(j) == a(j)(i),所以直接把上面公式中的i和j互换即可
  $$k=\frac{j(j?1)}{2}+i?1$$

🦋扩充：

• 当B数组下标从0开始，求出的a(i)(j)的下标，是和首元素相隔元素个数
• 数组下标其实是地址（指针）的映射，知道相差元素个数，再 * 单个元素字节大小，再加上起始地址（这里就是B[0]的地址），即可求得a(i)(j)在内存中的地址

📪1.2.1.2：下三角矩阵

下三角矩阵和对称矩阵存储思路大致相同，不同的在于：对上三角区域元素的存储上。因为上三角区域元素值均为相同的常值C，所以只用开一个存储空间来存储即可。所以相应的，三角矩阵的对应的B数组会多一个空间，来存储。也就是B数组的容量为：n(n+1)/2 + 1

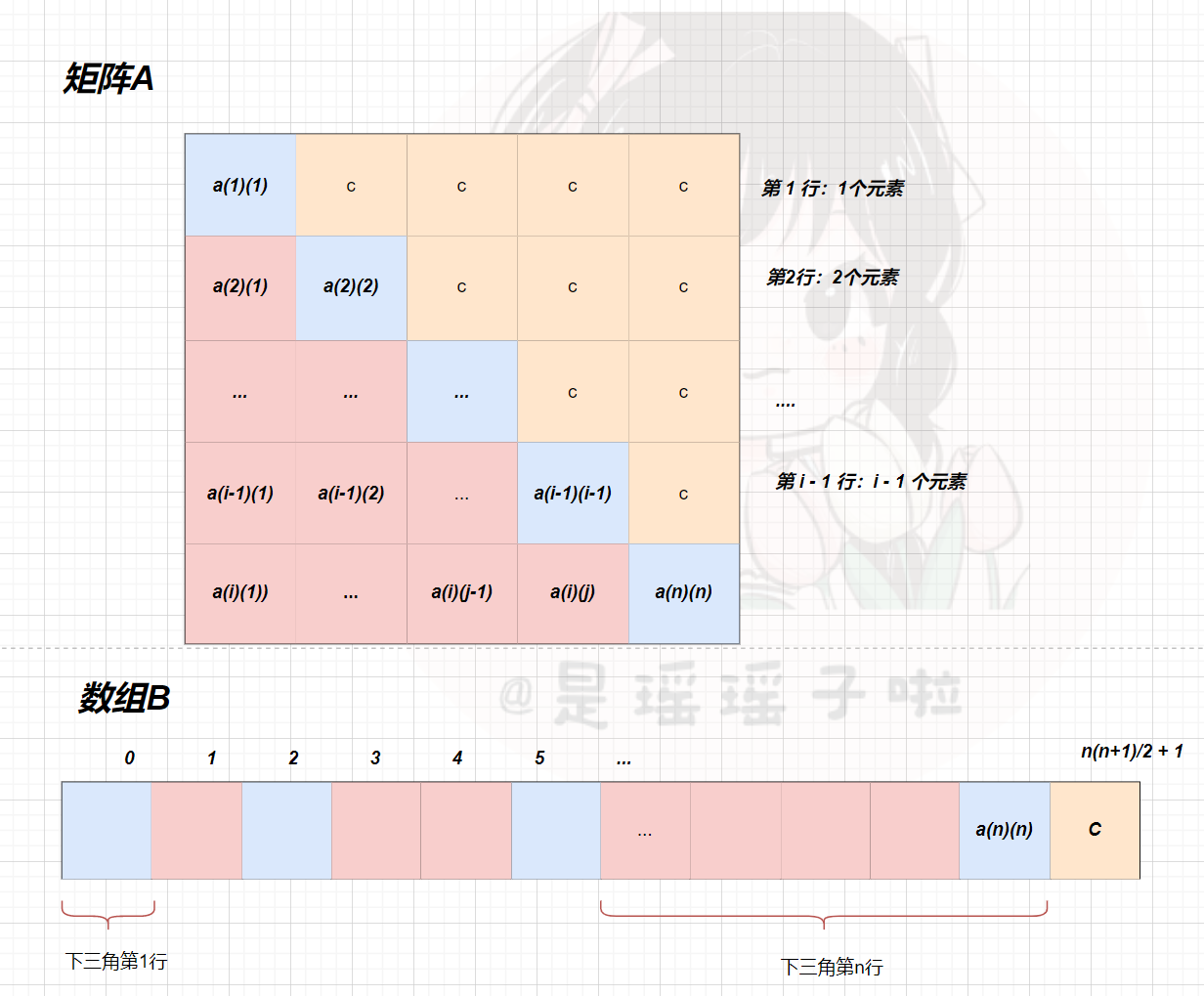
🌳压缩核心：求出a(i)(j)前面有多少个元素，0 + 相差元素个数（指针跳过中间相差元素个数），得到的就是a(i)(j)在B数组中的下标（其实也是地址的映射）;对于上三角区域的常值元素在B数组中都公用一个坐标
🥕公式 |a(i)(j)在B数组中的下标K：

• i >= j,下三角区域和主对角线元素

$$k=\frac{i(i?1)}{2}+j?1$$

• 对于上三角区域（j > i),a(i)(j) = c,这些元素全部在B数组的尾部的一个空间存储;前面有n(n+1)/2个元素，相应的坐标也是这么多
  $$k=\frac{n(n+1)}{2}$$

📪1.2.1.3：上三角矩阵

对于上三角矩阵，求解元素在B数组中的坐标的核心思路不变；上面求解比如a(i)(j)前面有多少个元素，都是按照***行优先***的规则（第一行填满，再接着下一行）；而对于上三角，我们采用***列优先***的方法

🥕公式 |a(i)(j)在B数组中的下标K：

• i <= j,上三角区域和主对角线元素

$$k=\frac{j(j?1)}{2}+i?1$$

• 对于上三角区域（j > i),a(i)(j) = c,这些元素全部在B数组的尾部的一个空间存储;前面有n(n+1)/2个元素，相应的坐标也是这么多
  $$k=\frac{n(n+1)}{2}$$

📍：三角矩阵——题目01

某n*n的矩阵A中，对角线以上的元素全为0。因此我们将对角线以下的元素 按行
存储在一个一维数组B中（下标均从1开始）。那么A[i][j]在一维数组B中的下标为（ ）。

A、 i*(i+1)/2 + j
B、i*(i-1)/2 + j - 1
C、i*(i+1)/2 + j - 1
D、i*(i-1)/2 + j?

🌳思路
因为B数组下标也是从1开始（我个人是这样理解的，如果一维数组的下标是从1开始，那么下标同时具有的含义是：这个元素为第几个元素）；所以，我们只用知道A[i][j]在下三角排列时，它是按行排列的第几个元素即可。那么就是先把行排满：(1 + i - 1) * (i - 1) / 2,再加上列的：j;所以i*(i-1)/2 + j即表示A[i][j]是第几个元素，同样表示它在B数组中的下标和第几个元素。

🙇?♀?注意

• 一定要注意，不管是矩阵A还是数组B，下标都是从1开始的！这点确实有点坑。如果A矩阵（看作二维数组）的第一个元素是从a[1][1]开始的话，且B数组下标从0开始，那么这题答案就是i*(i-1)/2 + j - 1！
• 这里因为是下三角，我们采用行优先的方式存储矩阵中的元素（从上到下，存完一行再存下一行）
• 如果是上三角（存储的元素位于矩阵的对角线以上包括对角线），采用列优先的方式存储（从右向左，存满一列再存下一列）
• 二维数组A[n][n]和A[0...n-1][0...n-1]的写法是等价的。如果数组写法为A[1..n]A[1..n],则说明指定了下标是从1开始存储元素。二维数组元素写为a[i][j],注意数组元素下标i和j通常是从0开始的。矩阵元素通常写为a i,j或者a(i),(j)，注意这时的i和j代表的行号和列号，都是从1开始的！
  

1.2.2：带状矩阵（三对角矩阵）

📪1)：描述

在矩阵中，所有非零元素都集中在以主对角线为中心的带状区域中。其中，最常见的是***三对角带状矩阵***

📪2)：非零a(i)(j)特点；

• i = 1(第一行，只有两个元素）：j = 1, 2
• 1 < i < n（中间行，每行有三个元素，j有三个取值）：j = i - 1, i , i +1
• i = n (最后一行，只有两个元素）： j = n-1, n

📪3)：压缩方法；
🕵??♀?①：确定存储该矩阵所需的一维存储空间（即一维数组B）的空间大小
每一行假设都有3个元素，但是由于第一行和最后一行只有两个，所以一维数组的容量为：3n - 2
🕵??♀?②：确定非零元素a(i)(j)在一维空间的下标（地址)
这里假设一维数组B的下标是从0开始，即首元素A[1][1]在B数组的下标是0，由此得出A[i][j]在B数组的下标为它前面的元素个数（A[i][j]和A[1][1]间隔的元素个数）

• 第i行中a(i)(j)前非0元素个数为：前 i - 1 行非零元素个数 + 第i行中非零元素个数 = 3（i-1）-1 + 第i行中非零元素个数
• 第i行中非零元素个数: j - i + 1
  • j - i = - 1 (j < i)
  • j - i = 0 (j = i)
  • j - i = 1 (j > i)

由此得到：A(i)(j)在B数组中的下标为（其中Loc(1)(1) = 0
$$Loc[i,j]=Loc[1,1]+(2(i?1)+j?1）$$

📍1.2：稀疏矩阵

稀疏矩阵是指矩阵中大多数元素为0的矩阵。从直观上来讲，当非零元素低于总元素的30%时，这样的矩阵称为稀疏矩阵

🤷?♀?稀疏矩阵有两种压缩存储方式：

• 三元组法
• 十字链表法

接下来我们分别来详细介绍这2种方法

1.2.1：三元组法存储稀疏矩阵

📪1)：三元组法的存储表示

🤔我们知道，稀疏矩阵中有许多0元素，存储这些非零元素大大浪费了空间。所以我们只用把非零元素存储下来，即可大大节省空间。那么如何存储呢？

三元组法，再通俗来说，就是给每个非零元素在存储自身的值的基础上再加两个域

• 行域：存储这个非零元素在原来的的矩阵中所占的行号
• 列域：存储这个非零元素在原来的矩阵中所占的列号

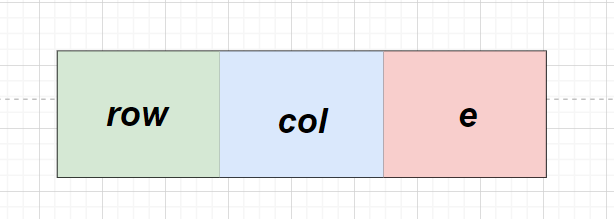
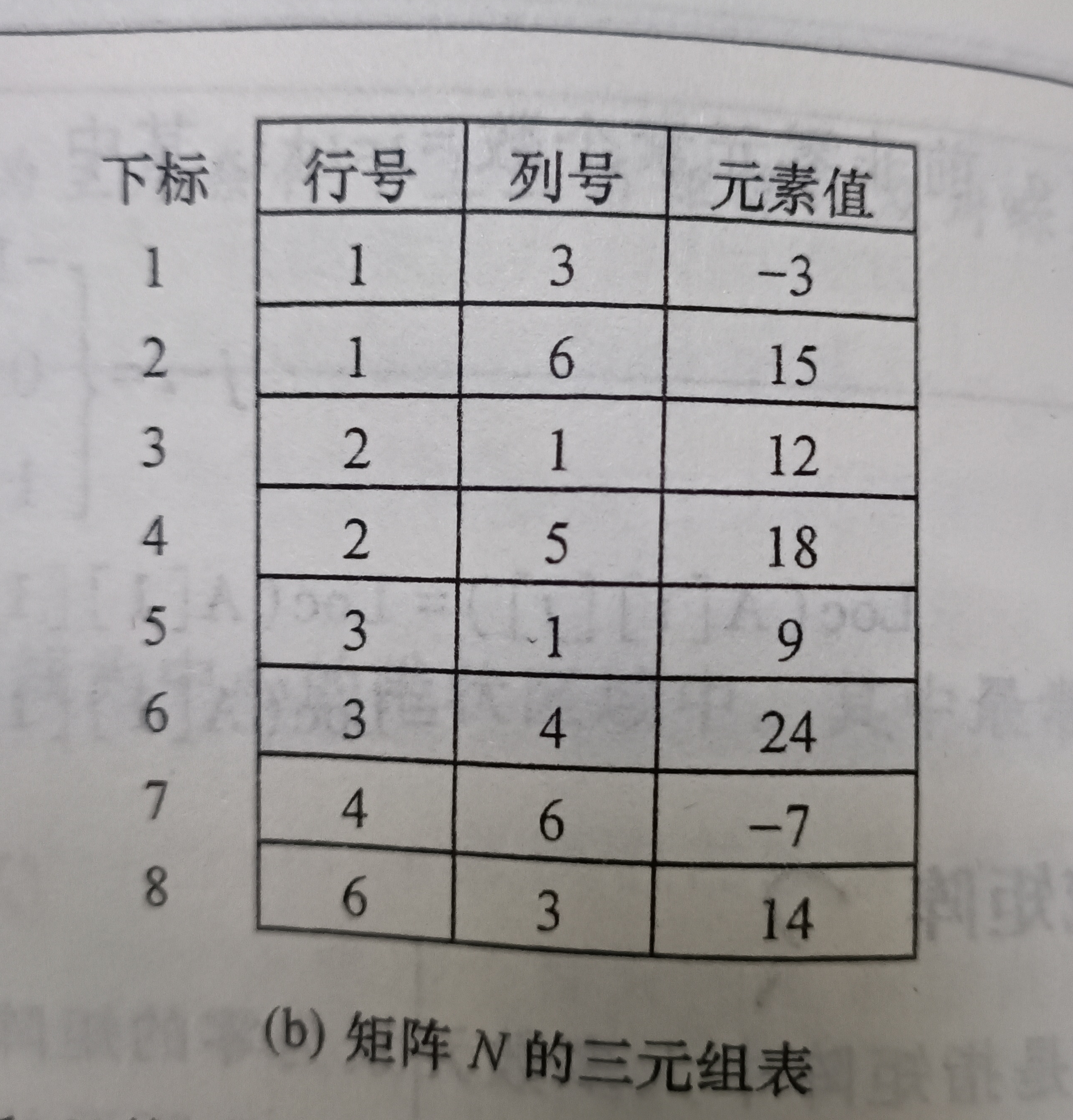
说明：为了处理方便，将稀疏矩阵中非零元素的三元组，按照行序为主序（行号为排序的第一关键字）、列号为第二关键字，进行排序。得到相应矩阵的三元组表

📪2)：三元组表类型定义

#define MAXSIZE 1000	//非零元素个数最多为1000

//三元组的定义，用于存储一个非零元素
typedef struct{
	int row,col;	//存储该非零元素的行和列
	ElementType e;	//存储该非零元素的值
} Triple;

//三元组表的定义
typedef struct{
	Triple data[MAXSIZE + 1];	//非零元素的三元组表。data[0]未用
	int m, n, len;	//原来矩阵的行数、列数、非零元素的个数
}TSMatrix;

1.2.1：十字链表法存储稀疏矩阵

🥕和用二维数组来存储稀疏矩阵相比，三元组表来存储稀疏矩阵大大节约了空间，且使得矩阵的某些运算（比如：矩阵的转置）的算法效率也提高。
🤔但是，当需要进行矩阵的加减乘除运算时，矩阵中非零元素的个数和位置可能会发变化甚至极大，那么三元组表为了保持：存储非零元素且以行序为第一关键字、列序为第二关键字，势必要移动、增加大量元素，这样是十分麻烦的。

🙋?♀?为了避免大量移动、增加元素，采用一种新的，压缩存储稀疏链表的方法：十字链表法。

📪1)：十字链表的存储表示

和三元组法存储矩阵相比，你可以把十字链表法叫作“五元组法”。为何这么说呢？
因为每一个非零元素节点，不仅有这3个域：（row , col , value).还增加了两个链域：

• right:链接同一行中的下一个非零元素
• down:链接同一列中的下一个非零元素

在十字链表中，同一行的的非零元素由于right指针，链接称为一个单链表。同一列的非零元素通过down指针链接成一个单链表。
所以某一个非零元素，既会属于某一行，也会属于某一列，行和列在这一点相交，像一个十字路口，所以这种方法根据这种形象的感觉，命名为：十字链表法。
同时，还需要设两个一维数组：

• 一个负责存储行的单链表的头指针
• 一个负责存储列的单链表的头指针
  
  🦋十字链表简单来说是通过链表来存储元素的。我们知道，和数组相比，链表在删除、移动、插入元素方面可是杠杠的，效率要比数组的效率高很多。正是这一点，解决了这一part开始所说的，由于非零元素的插入，需要大规模移动元素的问题。
  综上，十字链表能够灵活的插入由于矩阵的运算而产生的非零元素，删除因为矩阵运算而产生的新的零元素，实现矩阵的各种运算！

📪2)：十字链表类型定义

typedef struct OLNode{
	int row, col;	//非零元素的行号和列号
	ElementType value;
	struct OLNode *right, *down;	//非零元素所在行链、列链的后继指针域
}OLNode; * OLink;

typedef struct{
	OLink * row_head, *col_head;	//两个辅助一维数组，存储行链表、列链表的头节点
	//CrossList.row_head = (OLink *)malloc ( (m+1) ,sizeof (OLink));
	int m, n, len;	//存储原矩阵的行数、列数、非零元素个数
}CrossList;

---

• Java岛冒险记【从小白到大佬之路】
  
• LeetCode每日一题–进击大厂
• 算法