15.辐射度量学

1.为什么要学辐射度量学？

前面讲到的Blinn-Phong着色，Whitted-Style光线追踪都有一定问题，那就是它们并没有严格的按照物理规则定义各个变量。比如，Blinn-Phong中的光的强度，并没有一个确切的单位。同时Whitted-Style光线追踪我们也做了很多简化处理，例如能量的吸收衰减，我们只是凭借感觉直接的给了一个百分比，并没有严格按照物理规则计算和定义。而辐射度量学(radiometry)的方法能能更精确的给出我们这些信息(包括光线的定义以及表面材质与光线的作用)，从而达到更为真实的效果。

2.什么是辐射度量学？

辐射度量学描述了如何去描述光照，定义了一系列的方法和单位，可以给我们一些有关光照的各种属性（空间上的)，并且是基于几何光学来做的，认为光线是直线传播，不考虑光线的波动性

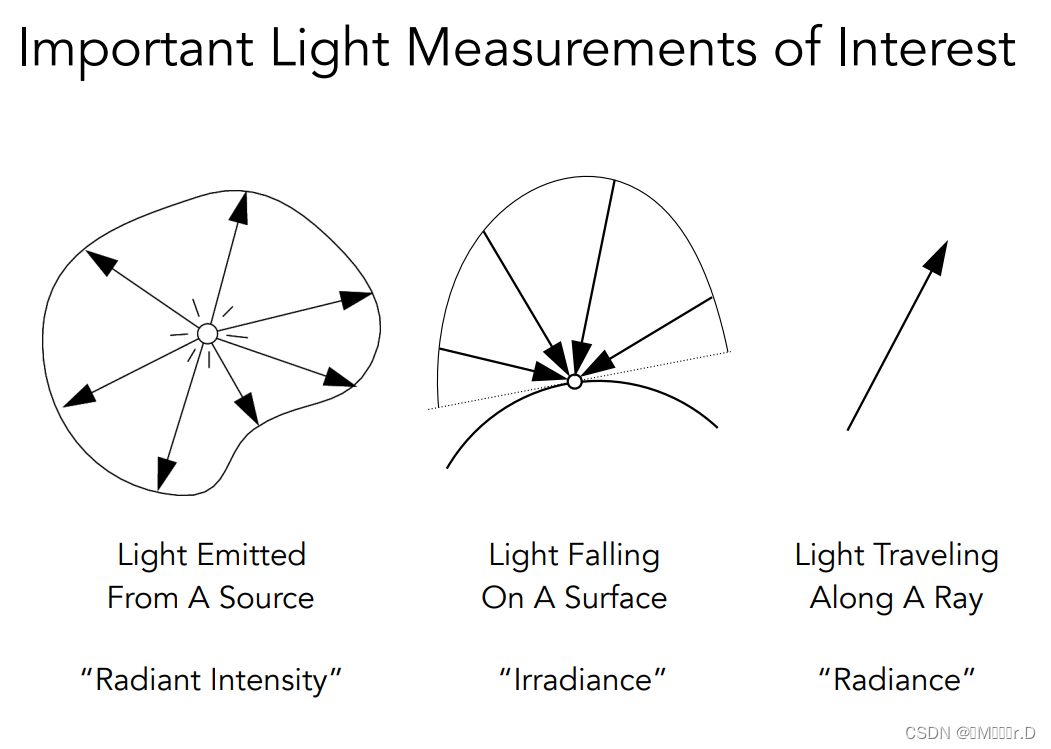
定义了光照的一些属性 ：Radiant flux（辐射通量）, intensity（辐射强度）, irradiance（辐照度）, radiance（辐亮度）

相当于在物理上准确定义光照的一个方法?

老师的个人学习路径：why → what →how（基本上是我们最容易忘得部分），how是最不重要的一部分

3.Radiant Energy and?Flux?(Power)—辐射能量和通量(功率)

Radiant Energy，辐射能，也就是能量，记作Q，单位J，焦耳，

Radiant Flux是什么呢，它表示辐射通量，用Φ表示，计算公式Φ=dQ/dt，单位W，瓦特，但这里表示的不是光的功率，虽然计算上面来讲是一样的，在光学中功率的单位用lm来表示，也就是lumen(流明)。而辐射通量我们可以简单的把它理解为光的“亮度”。辐射通量也可以理解成单位时间穿过某个平面的光子数量
?

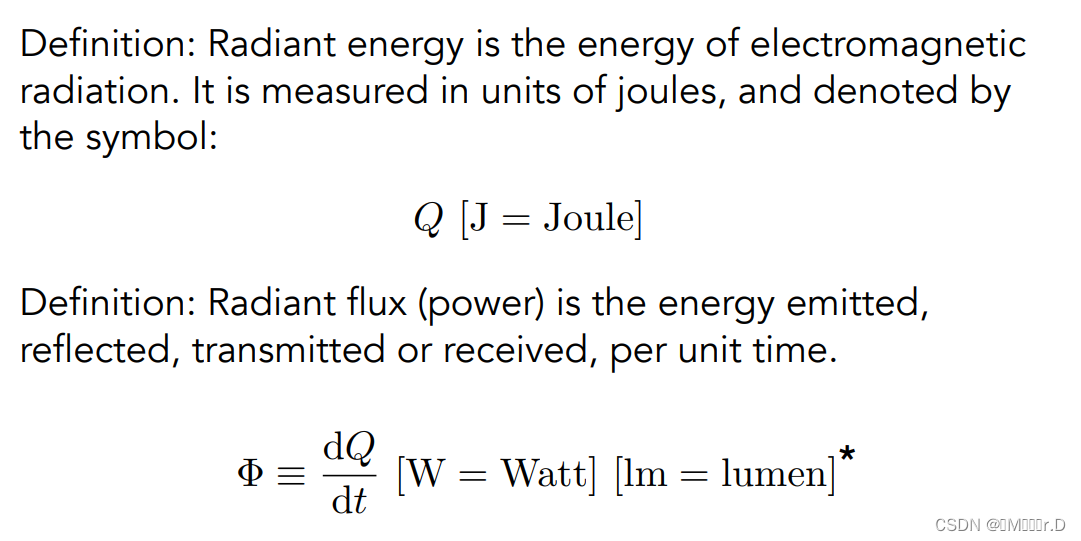
一些重要的物理量

4.Radiant Intensity—辐射强度

1.定义

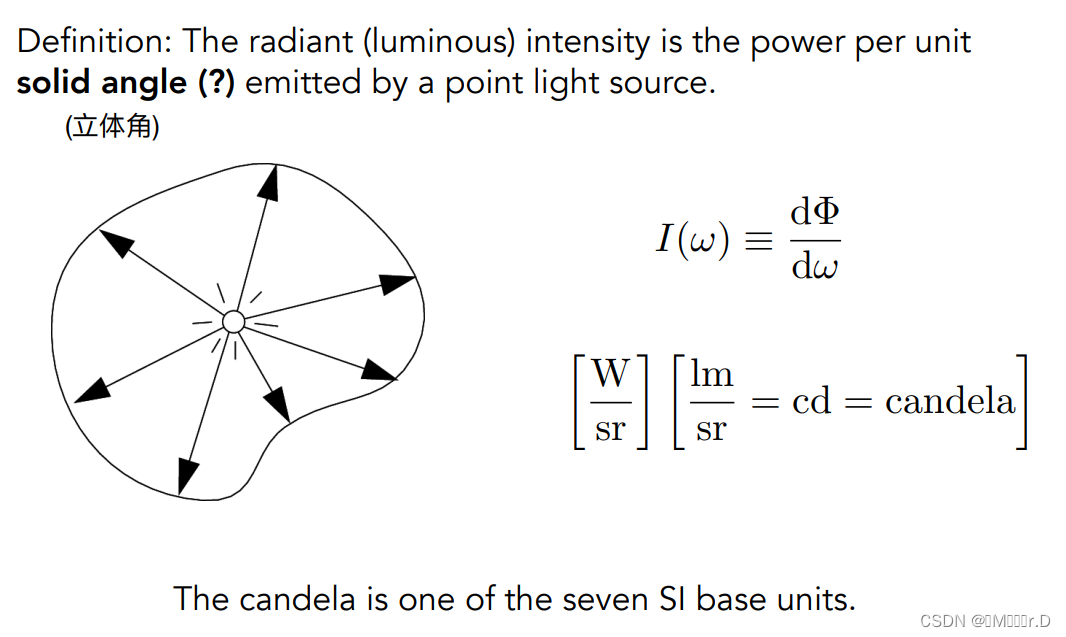
Radiant Intensity(辐射强度)：点辐射源在某方向上单位立体角内传送的辐射通量，记作I，即I(ω)=dΦ/dΩ，也就是说用单位辐射通量/单位立体角就是辐射强度。当然如果不是辐射通量是功率，也就是说单位是lm的情况下，那么它得到的单位叫candela简称cd。

2.立体角

平面几何中角的定义是用弧长l除以半径r，也就是弧度制，它很科学，因为如果圆等比例放大，那么弧长和半径也会等比例放大，那么l/r也就不变，角也就不变，这很准确。

立体角是在二维上进行了推广，也就是球表面上的一块小面积除以r的平方得到的就是立体角。显然整个球的立体角是4π。

单位立体角

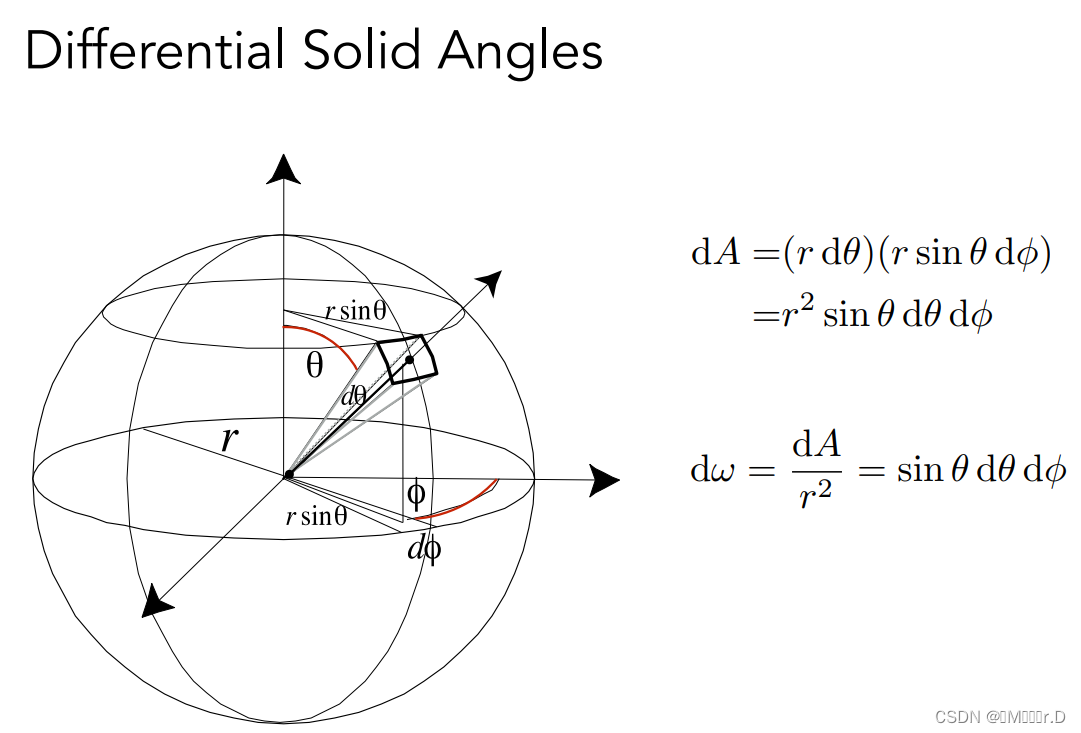
在一个球坐标中去定义，θ是距离z轴的角度，Φ是绕着z轴旋转形成的角度，根据这两个参数就可以表示球面上任何一个点。再想想立体角的定义，面积除以半径的平方，那么我们首先要把单位面积求出来(这里做了近似)，我们假定球面上的面积就是一个矩形的面积。那么就很容易得到单位面积dA=(r·dθ)(r·sinθ·dΦ)。求出之后再除以r的平方就得到单位立体角dω=sinθ·dθ·dΦ。这里理解不了可以直接记住结论也行。

如果我们对整个球的各个方向单位立体角做一个积分，得到的就是整个球的立体角也就是4π。

在整个辐射度量里面，可以用w来表示一个三维空间的方向。可以通过θ，Φ确定它的位置，进而可以求出单位立体角

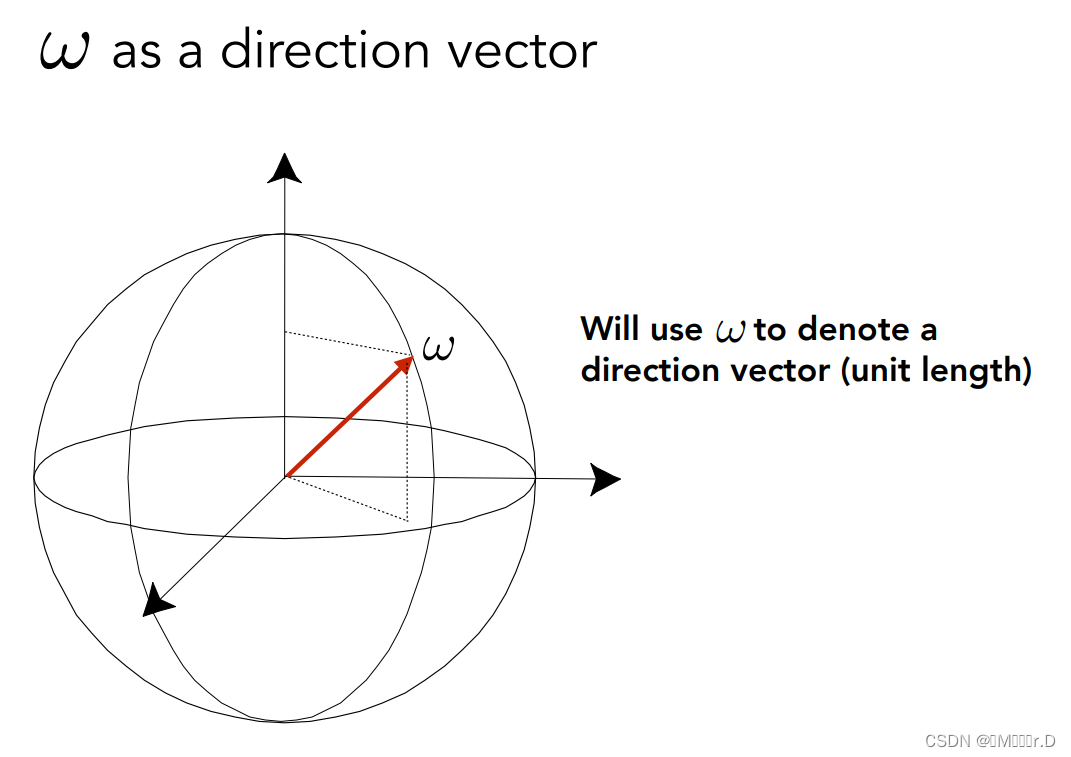
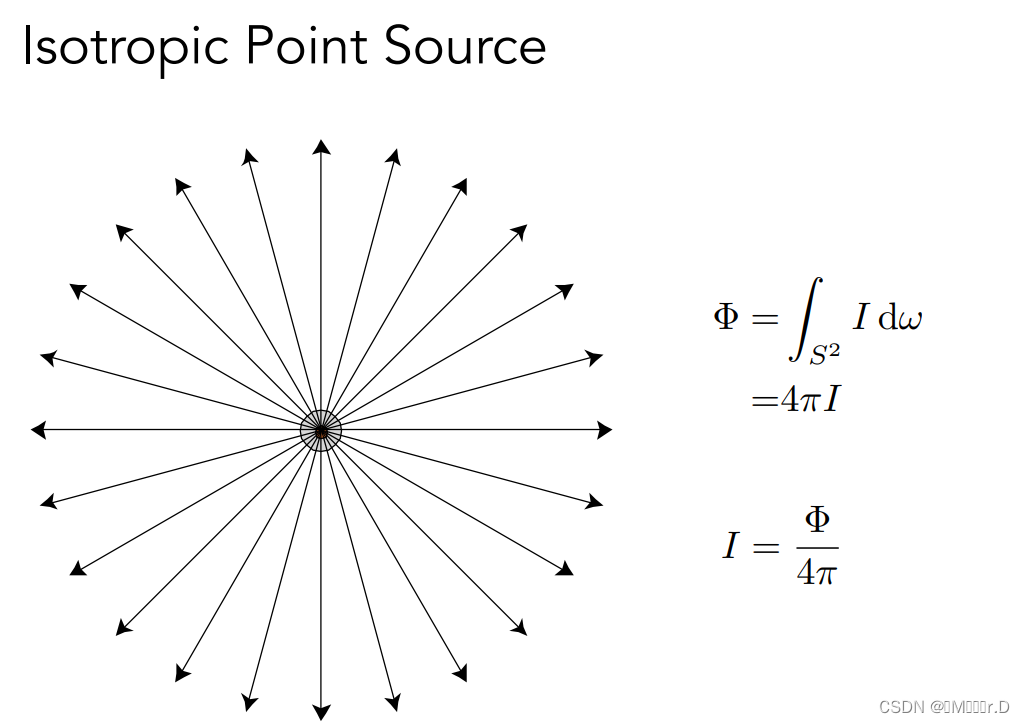
对于一个点光源，我们定义了它的辐射通量之后就可以利用我们之前说到的公式求出这个光源的Radiant Intensity(辐射强度)，这也表示，辐射强度实际上就是在任何一个方向上的辐射通量，也就是一个方向的亮度。

也就是说，当我们有一个均匀向四周发射光线的光源，我们完全可以用它的辐射通量Φ除以它的整个立体角4π，进而得到它任何一个方向上的Intensity，也就是辐射强度。

5.Irradiance—辐照度

1.定义

Irradiance，辐照度又称辐射照度，是受照面单位面积上的辐射通量，单位：瓦每平方米(W/㎡)。当然和Radiant Intensity相同，Irradiance也有流明与之对应的单位，是lux。

它和Intensity不同，Intensity是单位立体角内发射出的辐射通量，而Irradiance是单位面积内接收到的辐射通量。

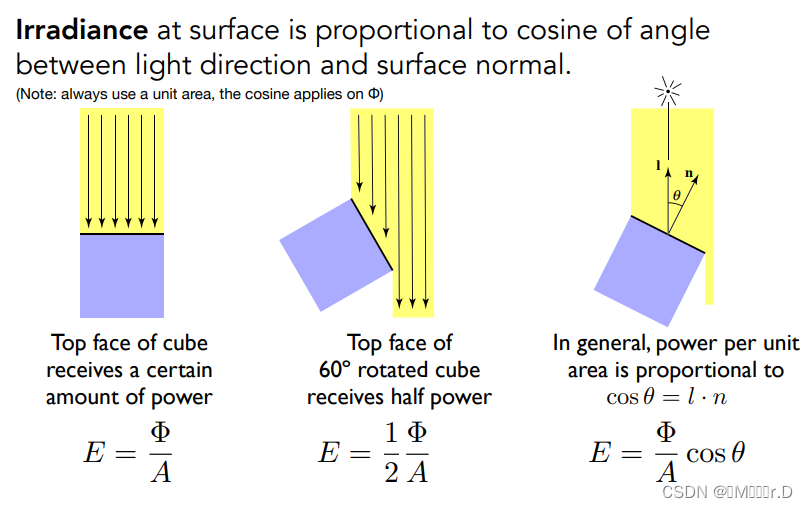
单位受照面的单位面积和我们之前提到的Lambert的规定类似，我们在这里规定的面积也要垂直于光线的方向，才能直接除以它的受照单位面积，否则要乘以cosθ。

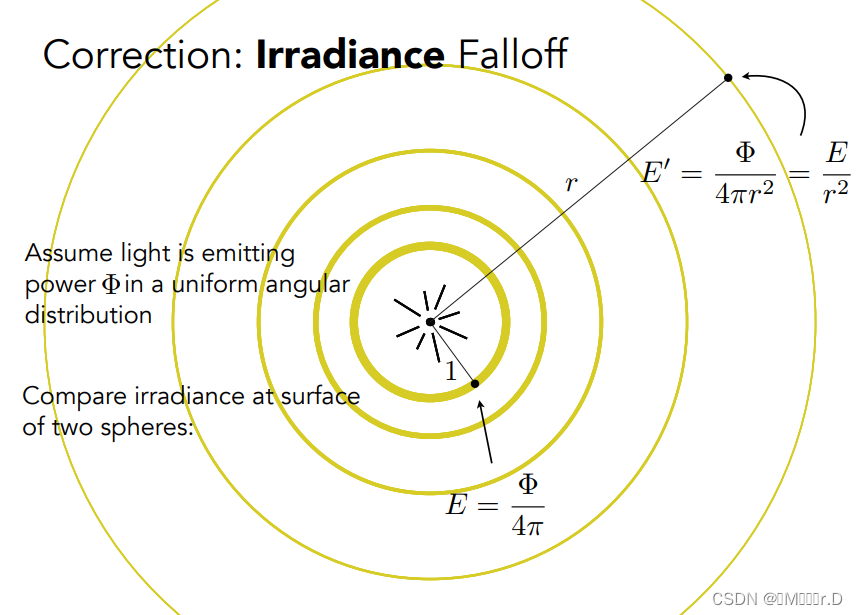
光线向四周发散均匀的分布在各个球壳上，而随着光传播距离越来越远，球壳面积越来越大，单位面积上分布的能量也就和r的平方成反比。这里的“能量”也就是Irradiance。而每个球壳上单位面积吸收的Irradiance也正是由辐射通量Φ除以球的表面积得到的，这也正是和r的平方成反比。

6.Radiance——辐亮度

1.定义

Radiance，辐射亮度简称辐亮度。是为了描述光线的各种属性。

单位立体角，单位面积上的辐射通量

简单的说，我们考虑dA(单位面积)接收的辐射通量，当以某一个单位立体角方向ω辐射出去，这个方向的能量是多少，就是Radiance。

可以把Radiance理解为单位立体角下的Irradiance，或者理解成单位面积下的Intensity。

2.入射辐亮度和出射辐亮度

单位立体角下的Irradiance可以有一个更形象的描述：Incident Radiance，入射辐亮度。如果Irradiance是指dA接收到某个方向的能量，而把它再除以单位立体角，也就是只考虑从某一个方向进到dA的能量被dA吸收了多少，也就是Incident Radiance。
出射辐亮度，也就是Exiting Radiance，我们定义的Intensity是单位立体角内的所有Radiance，而想要得到它的其中之一，则需要除以它所对应的面积也就是dA。

3.Irradiance和Radiance

我们常用的通常是Irradiance和Radiance的互相转化， 我们前面讲到了，两者相差的仅仅是方向性，对于任意一点p，它的Irradiance其中的一部分就是从某个立体角方向进入的Radiance，也就是dE，而如果把dE做一个积分就会得到它从单位半球接受的所有的立体角方向的Radiance，也就是最终的Irradiance。

7.Bidirectional Reflectance Distribution Function(BRDF)—双向反射分布函数

反射的理解：

理解1：光打到物体上，被弹走，改变方向

理解2：光打到物体表面，被吸收，再被发出

用Irradiance和Radiance解释理解反射

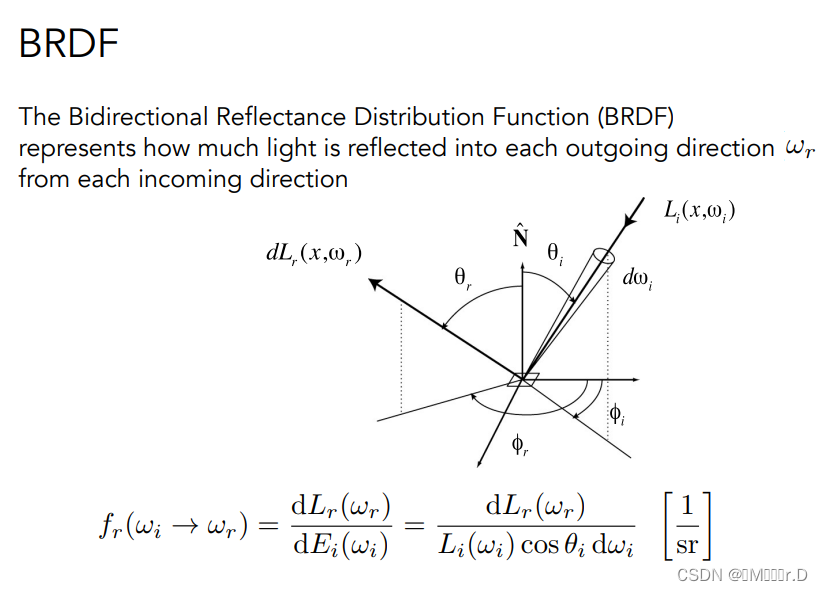
在一块单位面积从某一个立体角方向上接收的所有Radiance，也就是Irradiance，接着Irradiance又会朝各种方向辐射Radiance，对于任意一个出射方向，计算出它的Radiance，用它除以dA的Irradiance，这就是它反射出去的比例，简单地说就是用发射出去的Radiance去除以接收的Irradiance得到的一个比值。这也就是BRDF的定义。

BRDF的定义：对于任何一个出射方向，算出来他的Radiance，除以dA接受到的Irradiance，就是BRDF。

公式就如下图所写的，后面的sr是单位

实际上BRDF定义了不同的材质，也就是说不同的材质的BRDF中的所谓“比例”是不同的，也就导致了不同的材质与光线作用的不同。

8.反射方程

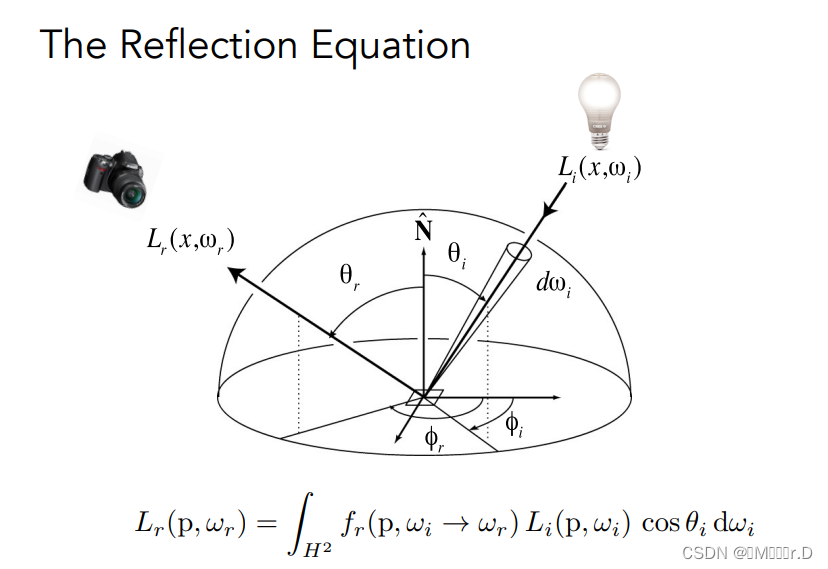
前面说的Radiance是某一个立体角方向发射而来并被接收的，那么我们对它做一个积分，就可以得到所有立体角方向射过来并被接收到的Radiance，也就是Irradiance再乘以我们的BRDF，我们就可以得到最终吸收了每一个立体角方向光线的能量然后从某一个方向反射出来的这个Radiance是多少。

简单地说，反射方程定义了一个着色点接受了环境中的能量后，从反射方向看去，它反射出的样子，也就是我们所说的Radiance(辐亮度)。

9.渲染方程

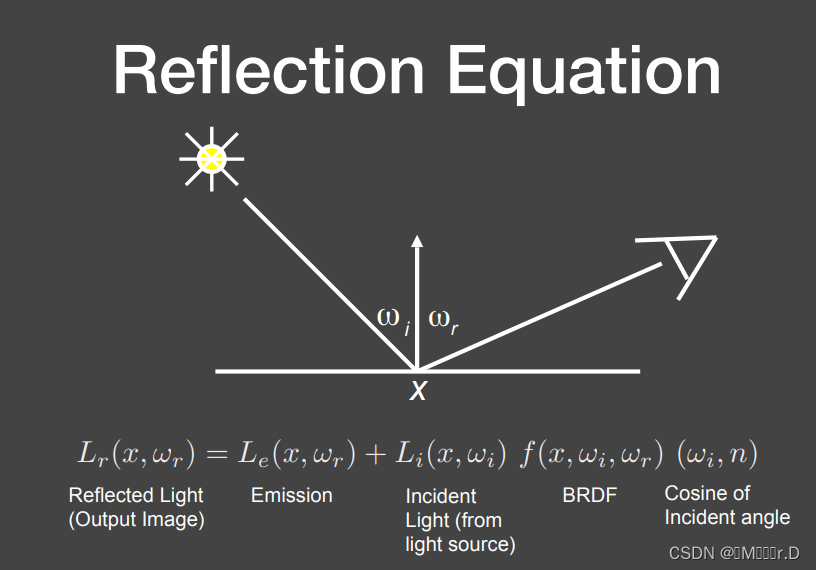
实际情况中物体还有自发光，需要在方程中加上这一部分。这就是渲染方程。已经可以解决限制在物体表面的光线传播问题了。

注意：

1.所有方向认为朝外（尽管我们认为wi是朝里的）

2.认为下半球贡献为0（定义积分忽略下半球）

3.n·ωi=cosθi

对渲染方程的理解

一个光和多个光的情况

多个光的话就把每个光的结果加起来

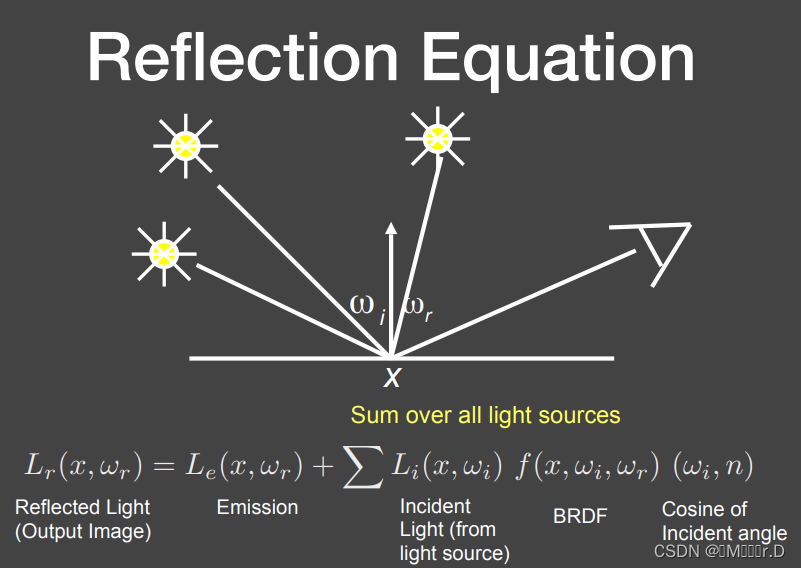
面光源的情况：面光源我们可以把它想象为一堆点光源的集合，然后我们同样计算它们从反射方向发出的Radiance。这样，BRDF项的求和就变成了积分。

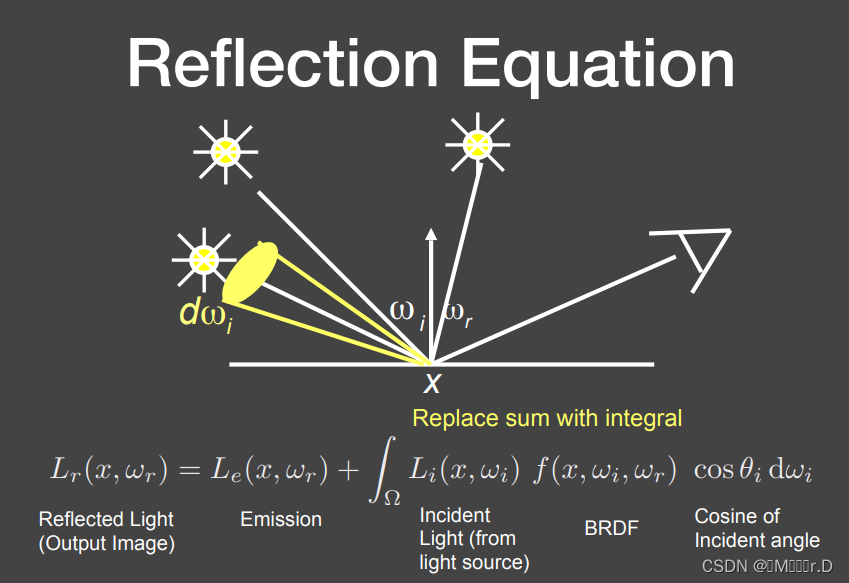
环境中还有一些其它的物体，它们会反射光源的光，然后同样影响我们看到的点。而实际上，无论是间接光源还是直接光源，我们都可以把它当成环境中影响x点的众多Radiance中的其中一个，也就是本质上来说，它们并没有区别。

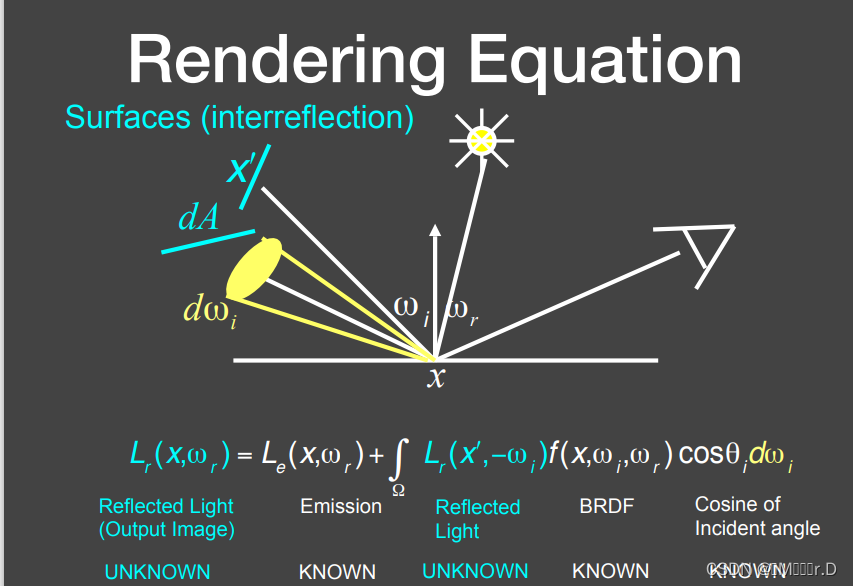
在整个渲染方程中，只有两个量我们不知道，一个是最终的结果，另一个则是各个反射出的Radiance。而其它的，如自发光，BRDF，夹角，在场景中我们都可以得到或定义好。那么我们就可以简化一步，得到简化后的渲染方程，u代表我们看到的方向，也就是反射方向，v代表入射方向，e代表自发光，l则代表Radiance，K则是反射操作符。

最后可以简化成一个极简的形式：L=E+KL(这里面涉及到线性代数的知识)，这也就代表着，我们看一个点发出的能量等于它自己发出的能量和经过该点反射出来的能量。在L=E+KL的表达式中，左边的L表示表面点x处的Radiance，右边的L表示从其他表面点处发射的光线打到x处的Radiance，并不是同一个物理量。

而写成L=E+KL的形式之后 ，移项，虽然(I-K)的逆是一个矩阵，但我们也可以进一步变换变成级数展开的一种形式。(实际上，将渲染方程中的L = E + KL转换成(I - K)L = E的过程中，我们并没有将两个不同的物理量合并成一个。相反，我们是将表面点x处的RadianceL(x,ωo)拆分成了两个部分：一部分是从表面点x处沿着方向ωo发射的光线的Radiance，另一部分则是从其他表面点处发射的光线到达表面点x处的Radiance。

级数展开公式

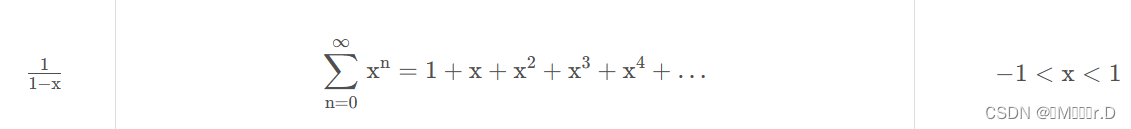
E：直接看到的光源（直接光照）

kE：辐射出的能量经过1次反射，会看到（间接光照）

kE2：经过2次反射

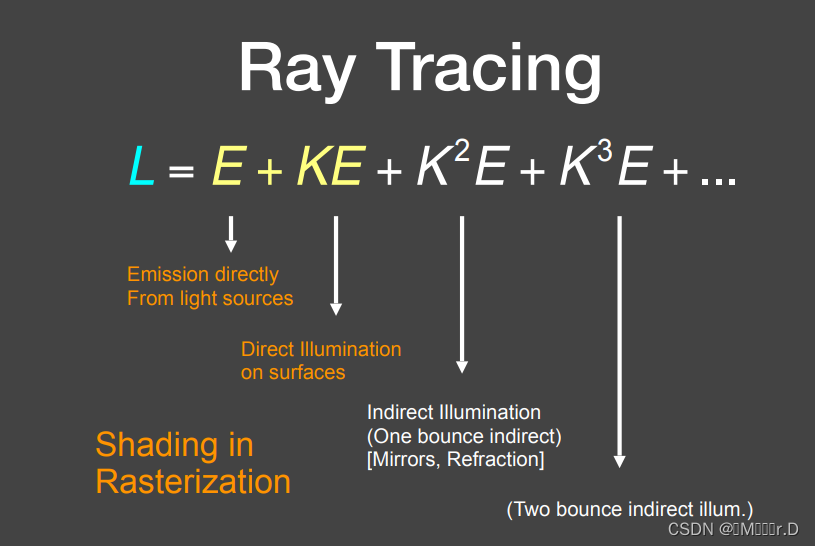
这个级数表示了所有可能的光线路径对辐射强度的贡献，包括直接光照和自发光、一次反射、两次反射、三次反射等等。这个级数中的每一项都可以使用类似于KL的积分形式来计算。而在实际应用中，我们通常只考虑级数中的前几项，因为随着反射和折射次数的增加，光线路径的数量呈指数级增长，计算量会变得非常大。因此，我们需要根据场景的复杂程度和渲染质量的要求来选择级数的截断点。

这样我们就可以理解全局光照了，全局光照，那也就是直接光照和间接光照的集合。

回顾光栅化，它只做了自发光E，和光线弹射一次KE的部分。当然现在光栅化也可以计算间接光照，只是要很麻烦

不同反射次数的对比

直接光照

直接光照+间接光照（额外弹射一次）

额外弹射4次

额外弹射16次

实际上到后面弹射次数对图像的影响已经不是很大了