北京交通大学高性能作业——多类积分函数华为鲲鹏 CPU 与 CPU + GPU 对比

1.description of the problem you have chosen

该课设主题是多类积分函数华为鲲鹏CPU 与 CPU + GPU 对比。
多类积分函数指的是在数学中，涉及到多重积分、固定常数、复杂的函数表达式等特点的一类积分函数。它们通常需要进行大量的数值计算和积分求解，以得出精确的结果。这些函数通常用于计算、模拟和数据分析等领域，并具有广泛的应用。在工程中，多类积分函数常用于电子设备设计、信号处理、通信系统优化、图像识别等方面，其中涉及到众多的复杂计算过程。
对于华为鲲鹏 CPU，它拥有强大的计算能力和超强的多线程性能，可以处理大量的计算任务。同时，鲲鹏 CPU 还具有高速的内存访问能力和大容量的内存，可以存储大量的数据。在处理多类积分函数时，鲲鹏 CPU 可以提供高效的计算能力，可以满足高性能计算的需求。
与此同时，华为鲲鹏 CPU 还可以与 GPU 联合使用，以进一步提高计算效率。GPU 具有高度并行的计算能力，可以同时处理多个任务，加速计算速度。在使用 GPU 计算时，可以采用并行化算法，充分发挥 GPU 的计算能力。此外，GPU 还可用于加速数据传输和存储，提高算法的整体效率。
因此，在处理多类积分函数时，华为鲲鹏 CPU与 CPU + GPU 的对比，取决于具体的算法和实现方式。对于一些计算密集型的算法，通过华为鲲鹏 CPU 的多线程计算加速可能会比 CPU + GPU 效果更好；但对于一些具有高并行性质的算法，CPU + GPU 的联合计算会提供更高的计算效率。另外，也需要考虑到算法的需求和计算平台的成本等因素。
在我的课设中，我选取了计算这个多类积分函数中的二重积分。在鲲鹏服务器上用直接计算和OMP技术来并行计算；在PC机上用CUDA（CPU + GPU）来计算，并比较了这些方法的性能，得出一系列结论。

2.description of the HUAWEI platform you use (including both software and hardware)

华为鲲鹏（Kunpeng）服务器是华为基于 ARM 架构体系设计的服务器，旨在为云计算、大数据、虚拟化等业务提供高性能、高可靠性的硬件平台。它采用了充分优化的 CPU 和操作系统软件，提供超强的性能和可扩展性，同时还支持多种高速网络接口和存储设备，可以满足各种企业和机构的计算需求。
鲲鹏服务器的硬件部分主要具有以下特点：
·可扩展、高密度的服务器架构
鲲鹏服务器支持双路主板设计，可扩展高达 64 个处理器核心。它还具有高密度的服务器设计，可在标准机架尺寸下实现高达 128 个核心和 2TB 内存。
·领先的处理器性能
鲲鹏服务器采用最新一代 ARMv8-A 架构中的 APM 扩展，可实现每核心 2.6GHz 的峰值处理器性能。此外，其加速器支持 SIMD 指令集，提供更高效的向量运算支持。
·多种高速接口
鲲鹏服务器支持多种高速网络接口，包括 40G/100G 以太网、InfiniBand 和 RoCE 等。它还支持多种存储设备，包括高速硬盘、SSD 和 NVMe 设备等。
·高可靠性设计
鲲鹏服务器采用了多种高可靠性设计，包括 ECC 内存、RAID 存储、双路热备份等。此外，它还支持预测性故障诊断和动态电源管理等功能，提供更高的可靠性和稳定性。

鲲鹏服务器的软件部分也是其优势之一，其操作系统基于 ARM 架构，并专为企业级应用定制。这个操作系统称为 EulerOS，其特点如下：
·自适应架构
EulerOS 具有自适应架构，可以运行于 ARM 和 x86 架构的服务器上，为用户提供无缝的跨平台支持。
·安全性和可靠性
EulerOS 支持基于 TPM、SELinux、AppArmor 等多种安全技术，并经过了多层认证和安全审计，可以确保每个用户和每台服务器的安全和可靠性。
·模块化设计
EulerOS 采用模块化设计，可以根据用户需求进行轻松部署和管理，提高了用户的效率。
总体来说，华为鲲鹏服务器提供了高性能、高可靠性、高扩展性和高安全性的硬件和软件平台，可以为用户提供更高效、更可靠的计算服务。

3.your algorithm flow chart

直接计算流程图

图3-1

OpenMP计算流程图

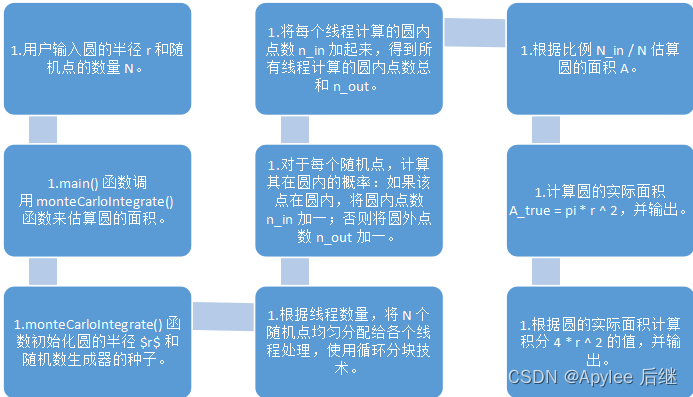
图3-2

CUDA计算流程图

图3-3

4.analysis of the key parallelism in your code (source code in attachment )

omp实现的并行性分析

• 线程并行性
  在主函数调用的 monteCarloIntegrate 函数中，通过使用 #pragma omp parallel 告诉编译器该区域需要进行并行化处理。这样编译器会自动根据环境中的核心数生成对应的线程，在多线程环境下同时执行对应的代码块。这种线程并行方式具有一定的并发度，可以利用多核 CPU 提高程序计算效率。
• 循环并行性
  程序中的循环部分使用了 #pragma omp for 实现循环并行化，OpenMP 根据循环次数自动将其划分成若干个任务块，并将其分配到不同的线程中进行运算，每个线程运算完自己的任务块后，将结果累加到主计算线程的结果中，最后得到完整的蒙特卡罗积分结果。使用循环并行化技术时，需要注意数据依赖关系是否正确，避免线程之间出现数据争用等问题。
• 动态调度策略
  程序采用了动态调度策略实现块划分的并行，即 schedule(dynamic)，这种策略可以在运行时实时根据程序的负载情况对任务进行动态分配，而不是一开始就静态地将任务均分给执行线程，从而更加有效地平衡各个线程的负载，避免出现空闲现象，提高计算效率。
• 临界区并行性
  程序使用了 #pragma omp critical 指令实现了临界区并行化，即在多个线程同时访问同一个临界区时，需要保证同一时刻只有一个线程进入临界区处理。该指令防止了不同线程之间的数据竞争和并发错误。
• 硬件特性的并行性
  程序中没有明显地应用硬件特性对程序进行优化，例如采用SIMD指令集或者使用多线程访问磁盘。如果需要优化程序，可以使用硬件特性进行任务加速和优化，从而更加高效地完成蒙特卡罗积分计算。

CUDA实现的并行性分析

• CUDA 架构的并行性
  这些代码利用了 NVIDIA CUDA 架构提供的并行处理能力。CUDA 可以利用大量的可编程 GPU 计算核心并行执行操作，加速运算速度。在以上代码中，程序使用了多个 CUDA 线程来并行计算蒙特卡罗积分，其中每个线程都独立执行随机采样，并将圆内的点数累加到计数器中。这种方式可以有效提高计算速度和准确度。
• 数据并行性
  以上代码通过数据并行性来提高计算速度。CUDA 开发中，数据并行性是常见的并行计算方式之一。具体而言，数据并行性利用多个 CUDA 线程同时计算大规模数据集，通常分解为一系列的小任务，每个线程计算其中的一部分。在本题中，程序使用多个 CUDA 线程同时计算蒙特卡罗积分，每个线程独立采样和累加圆内点数，最终将结果通过巧妙的算法计算出最后的积分结果。这种计算方式类似于分布式计算，能够大大提高可编程GPU 的计算性能。
• 并发初始化
  这段代码还利用了 CUDA 并发初始化的功能，从而实现了高效的数据初始化。在蒙特卡罗积分运算中，需要为每个 CUDA 线程初始化 curand 的状态，以产生随机样本，从而计算区域面积。通过 CUDA 的并发初始化，程序可以实现高效的数据初始化，从而加速整体计算速度。
• 内存读写并行性
  此外，以上代码还利用了内存读写的并行性来提高系统性能。使用 CUDA 进行计算时，通常需要通过主机代码调用 API 操作来完成内存的读写操作。通过多个 CUDA 线程并发执行这些操作，程序可以利用更多的硬件资源和宽带而大大提高内存读写效率。完整的程序按照一种良好的并发性模式，从而实现高效的蒙特卡洛积分计算。

5.your test scheme

方案1：直接计算

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <random>
#include <chrono>
#include <omp.h>
#define ull unsigned long long 

double monteCarloIntegrate(double r, ull N) {
	double _sum = 0.0;
	//修改随机数生成器
	unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
	std::mt19937 gen(seed);
	std::uniform_real_distribution<> dis(0, r);
	double x, y;
	for (ull i = 0; i < N; ++i) {
		x = dis(gen);   // 随机生成 x
		y = dis(gen);
		if (x * x + y * y <= r) {
			_sum += 1.0f;
		}
	}
	return _sum;
}

int main() {
	double r;
	printf("请输入积分上下限！\n");
	scanf("%lf", &r);

	const ull n = 1e8;  // 投点个数
	clock_t before, after;
	before = clock();
	double res = monteCarloIntegrate(r, n);
	double realres = (res / n) * 4 * r * r;
	after = clock();
	printf("The value of integration is %20.18f\n", realres);
	printf("The time to calculate integration was %f seconds\n", ((double)(after - before) / CLOCKS_PER_SEC));

	return 0;
}

方案2：OMP并行计算

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <random>
#include <chrono>
#include <omp.h>
#define ull unsigned long long 

double monteCarloIntegrate(double r, const ull N) {
	double _sum = 0.0;

	//修改随机数生成器
	unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
	std::mt19937 gen(seed);
	std::uniform_real_distribution<> dis(0, r);

	//使用循环分块技术
#pragma omp parallel
	{
		double sum = 0.0;	//在每个线程内部定义一个sum用来累计该线程计算的击中的次数
#pragma omp for schedule(dynamic) nowait
		for (ull i = 0; i < N; ++i) {
			double x = dis(gen);
			double y = dis(gen);
			if (x * x + y * y <= r * r) {
				sum += 1.0;
			}
		}
#pragma omp critical
		//将每个线程的结果累加给_sum
		_sum += sum;
	}

	return _sum;
}

int main() {
	double r;
	printf("请输入积分上下限：\n");
	scanf("%lf", &r);
	const ull n = 1e8;
	clock_t before, after;

	before = clock();
	double res = monteCarloIntegrate(r, n);
	double realres = (res / n) * 4 * r * r;
	after = clock();
	printf("Integration value is %20.18lf\n", realres);
	printf("Running time was %lf seconds\n", ((double)(after - before) / CLOCKS_PER_SEC));
	return 0;
}

方案3：CUDA（CPU + GPU）并行计算

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <random>
#include <cuda.h>
#include <curand_kernel.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#define NUM_THREAD 1024
#define NUM_BLOCK 32 // 修改块数以适应更大的计算量
#define ull unsigned long long 

using namespace std;


// CUDA 核函数，计算蒙特卡洛积分
__global__ void monteCarlo(curandState* state, double* _sum, ull n, float r, ull nthreads, ull nblocks) {
    ull tid = threadIdx.x + blockDim.x * blockIdx.x;    //线程唯一的标识符
    curandState localState = state[tid];    //每个线程都有一个随机数状态号
    float x, y;

    for (ull i = tid; i < n; i += nthreads * nblocks) {
        x = curand_uniform(&localState) * r;    //给x分配一个从0-1的随机数
        y = curand_uniform(&localState) * r;    //给y分配一个从0-1的随机数
        if (x * x + y * y <= r * r) {
            _sum[tid] += 1.0f;  //如果在圆内，就+1
        }
    }

    state[tid] = localState;    //线程结束的时候需要收回这个状态号，方便下一个线程分配随机数
    //最终_sum累积的是，是在四分之一圆的次数
}

__global__ void init_states(unsigned int seed, curandState* states) {
    int tid = threadIdx.x + blockIdx.x * blockDim.x;
    curand_init(seed + tid, tid, 0, &states[tid]);
}

int main() {
    // 设置CUDA相关变量
    float r, res = 0, realres = 0;
    printf("请输入积分上限！\n");
    scanf("%f", &r);
    const ull n = 1e11; // 增加采样点数量，提高计算精度

    // 为每个线程初始化 curand 状态
    curandState* devStates;
    cudaMalloc((void**)&devStates, NUM_THREAD * NUM_BLOCK * sizeof(curandState));

    //线程总数
    ull size = NUM_THREAD * NUM_BLOCK * sizeof(double);
    //sumHost是host端的总和，sumDev是device端的总和
    double* sumHost, * sumDev;
    sumHost = (double*)malloc(size);
    memset(sumHost, 0, size);

    cudaMalloc((void**)&sumDev, size);

    // 不需要再次将 sumDev 初始化为 0，因为 CUDA 分配出来的内存本身已经被初始化为 0。

    clock_t before, after;
    before = clock();

    dim3 numBlocks(NUM_BLOCK, 1, 1);
    dim3 threadsPerBlock(NUM_THREAD, 1, 1);

    //初始化device端状态号
    init_states << <numBlocks, threadsPerBlock >> > (time(nullptr), devStates);

    monteCarlo << <numBlocks, threadsPerBlock >> > (devStates, sumDev, n, r, NUM_THREAD, NUM_BLOCK);

    cudaMemcpy(sumHost, sumDev, size, cudaMemcpyDeviceToHost);

    for (ull tid = 0; tid < NUM_THREAD * NUM_BLOCK; tid++) {
        res += sumHost[tid];
    }

    //次数除以总数 * 4，得到二重积分值
    realres = (res / n) * 4 * r * r;
    after = clock();

    printf("The value of integration is %20.18lf\n", realres);
    printf("The time to calculate integration was %lf seconds\n", ((double)(after - before) / CLOCKS_PER_SEC));

    free(sumHost);
    cudaFree(sumDev);
    cudaFree(devStates);

    return 0;
}

6.screenshots of your experiment results and analysis of the experiment results

直接计算

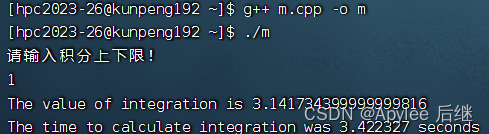
图6-1 取样1e7，上限1


图6-2 取样1e8，上限1


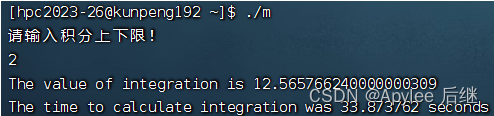
图6-3 取样1e8，上限2

OpenMP计算

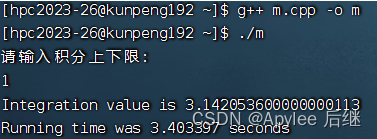
图6-4 取样1e7，上限1

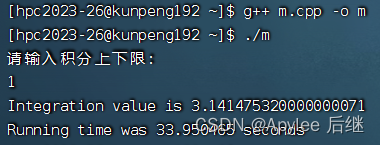
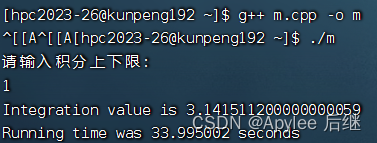
图6-5 取样1e8，上限1

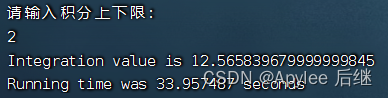
图6-6 取样1e8，上限2

CUDA并行计算

图6-7 取样1e10，上限1



图6-8 取样1e11，上限1


图6-9 取样1e11，上限2

结果分析

首先，上限为1时，结果为pi，值为3.1415926……；上限为2时，结果为4*pi，值为12.5663704……。不论是直接计算，OpenMP计算还是CUDA计算，误差都在正常范围内，正确性满足。
直接计算和OpenMP计算准确率比较。两者在准确率方面都差不多，基本上精确到第三位小数。这也因为使用了1e8的取样量，对于1e7的取样量，肯定会导致只精确到第二位小数。
两者在性能上来讲，在OpenMP作为支持并行计算的库，并没有比直接计算快。一方面因为华为鲲鹏虽然在计算上是非常快，性能极高的。但是它终究还是CPU，发挥不出很多OpenMP的实力。另一方面，可能在线程建立与销毁上面也会花费一定时间。OpenMP计算内容只有一个加法，不是很复杂，所以也导致了时间上差不多。
CPU+GPU与CPU准确率比较。因为CUDA选取的是1e10，1e11取样，这让CUDA计算能够精确到小数点后四位。
性能上因为CUDA本身使用的GPU+CPU，充分利用的大批线程并行计算的优势，将单线程计算的复杂度降低了很多，所以在速度上，即使CPU样本量1e7,CUDA样本量1e11，也丝毫不逊色于CPU。性能上远超CPU。

7.your project summary

在这个项目中，我使用了蒙特卡罗积分算法来计算二重积分，并通过并行化技术来提高程序的计算效率。我分别使用了 OpenMP 和 CUDA 工具库来并行化代码，并对两种并行化技术进行了比较。
在实现中，我遇到了一些报错的问题，这让我感到非常沮丧和困惑。我花费了很长时间仔细检查代码，包括变量名、数据类型和代码结构等，最终找到了一些不当之处，并成功解决了错误。最令我头疼的是下面这段代码：

void GenRandomX(float* X, float a, float b, int N) {
    for (int i = 0; i < N; i++) {
        std::random_device rd;
        std::mt19937 gen(rd());
        std::uniform_real_distribution<> distrib(a, b);
        //其中，rd() 创建一个 random_device 对象，gen(rd()) 创建一个名为 gen 的随机数引擎，并以 rd() 为构造函数的参数初始化。distrib(a, b) 创建一个在 a 至 b 之间均匀分布的随机数分布器。distrib(gen) 调用生成器 gen，返回一个随机数，该随机数在 distrib 指定的范围内。
        X[i] = distrib(gen);
    }
}

这段代码我其实是想做一个随机化的计算，这刚好满足蒙特卡罗的方式，但是在CUDA下，这个X随机数数组导入到核函数计算之后，不论怎么样，计算结果都是0；经过两天的调查，我才发现，原来要用到CUDA中自带的随机生成器！！！真的又兴奋又难过的感觉。
通过本项目，我学到了很多关于并行化和优化算法的知识。蒙特卡罗积分算法本身是一种简单而有效的积分算法，它可以用于计算各种类型的积分。将其与并行化技术相结合，可以更有效地加速程序，并提高准确性。使用 OpenMP 和 CUDA 实现代码的并行化可以极大地加快程序的运行速度，但是需要注意算法并行化的正确性和数据竞争的问题。不过因为CUDA是基于我PC机上的GPU，通过分配线程块来并行计算，极大地提高的性能。OpenMP 可能因为我的理解不够深刻，它的性能没有想象中的那么理想。也证明了CUDA的强大之处。
总的来说，这个项目让我更深入地了解了并行编程、数值方法和优化算法等方面的知识，也提升了我的代码调试能力。虽然我遇到了一些困难，但是通过不断的尝试和调整，最终还是得以成功实现了代码的修改和优化。在今后的学习和工作中，我将继续努力深入理解并行计算的相关知识，以便更好地实现高效的算法。