【优选算法】专题四:前缀和(一)

DP34 【模板】前缀和

DP34 【模板】前缀和

此方法的时间复杂度是O(Q)+O(N);

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 1. 读入数据
        int n=in.nextInt(),q=in.nextInt();
        int[] arr = new int[n+1];
        for(int i =1;i<=n;i++)arr[i] = in.nextInt();

        // 2. 预处理一个前缀和数组
        // 此处避免数字加和太大,我们使用long类型
        long dp[] = new long[n+1];
        for(int i=1;i<=n;i++)dp[i] = dp[i-1]+arr[i];

        // 3. 使用前缀数组
        while(q>0){
            int l=in.nextInt();
            int r=in.nextInt();
            System.out.println(dp[r]-dp[l-1]);
            q--;
        }
    }
}

DP35 【模板】二维前缀和

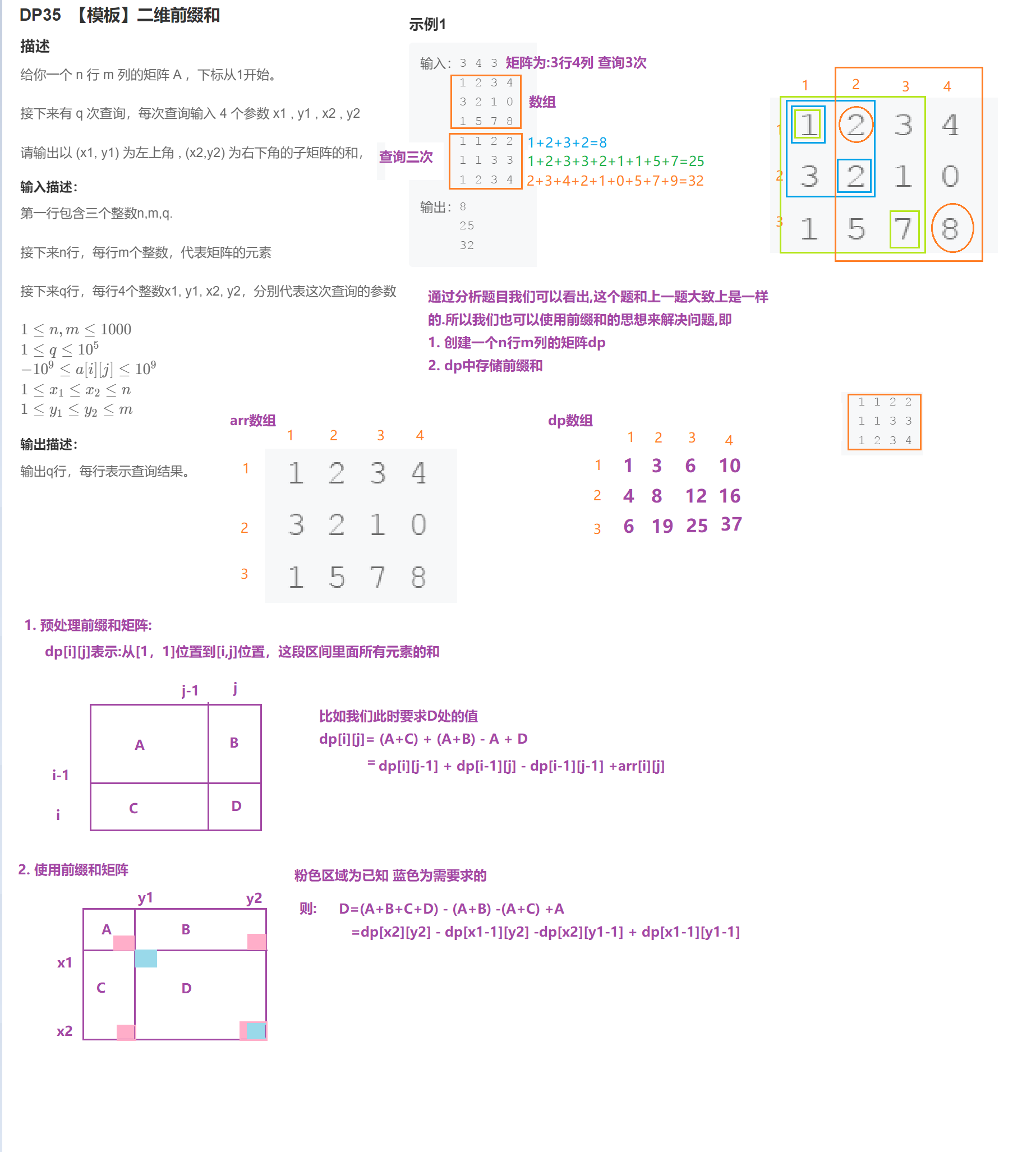
DP35 【模板】二维前缀和

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 1. 读入数据
        int n=in.nextInt(),m=in.nextInt(),q=in.nextInt();
        int[][] arr = new int[n+1][m+1];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                arr[i][j]=in.nextInt();
            }
        }

        // 2. 预处理一个前缀和矩阵
        long[][] dp=new long[n+1][m+1];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+arr[i][j];
            }
        }

        // 3. 使用前缀和矩阵
        while(q>0){
            int x1=in.nextInt(),y1=in.nextInt(),x2=in.nextInt(),y2=in.nextInt();
            System.out.println(dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]);
            q--;
        }
    }
}

724.寻找数组的中心下标

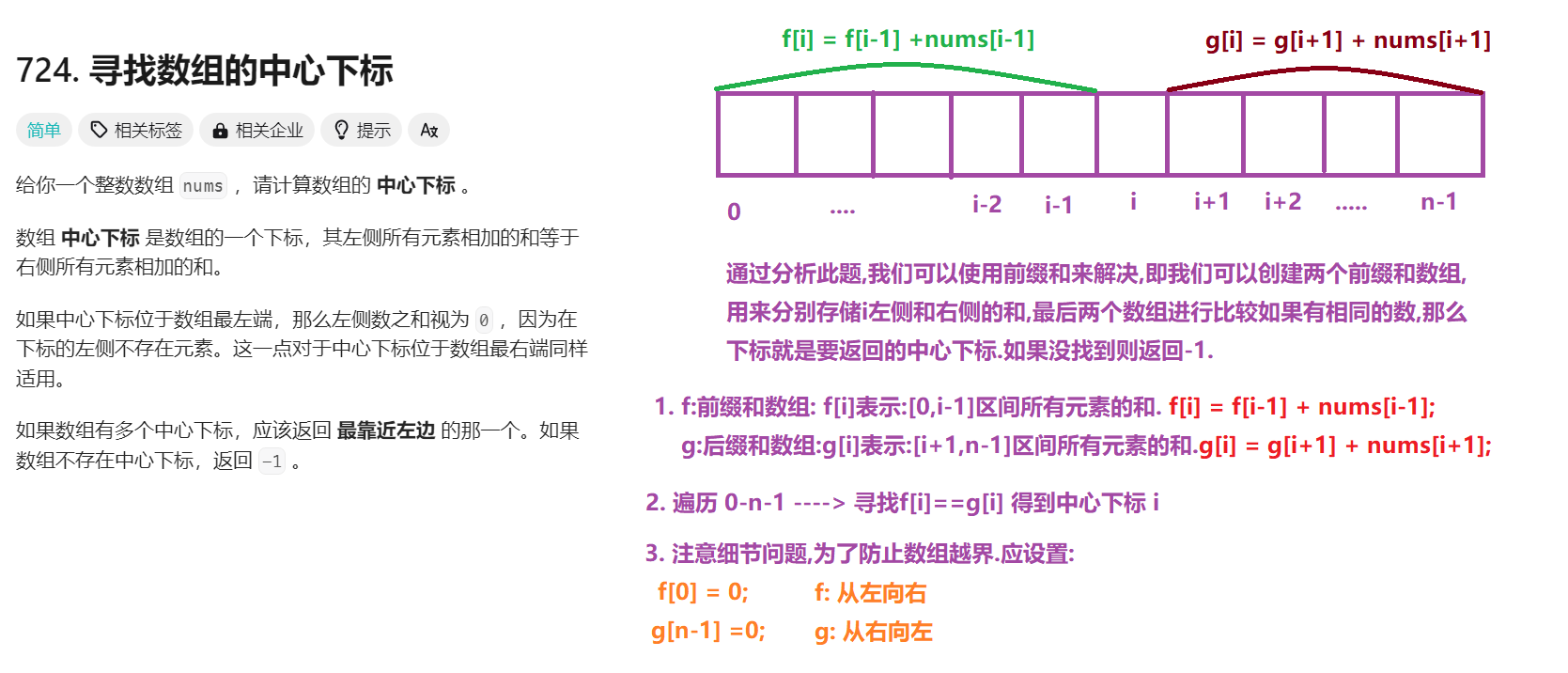
724.寻找数组的中心下标

class Solution {
    public int pivotIndex(int[] nums) {
        int n=nums.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0]=0;
        g[n-1]=0;
        for(int i=1;i<n;i++){
            f[i]=f[i-1]+nums[i-1];
        }
        for(int i=n-2;i>=0;i--){
            g[i]=g[i+1]+nums[i+1];
        }
        for(int i=0;i<n;i++){
            if(f[i]==g[i]){
                return i;
            }
        }
        return -1;
    }
}

238.除自身以外数组的乘积

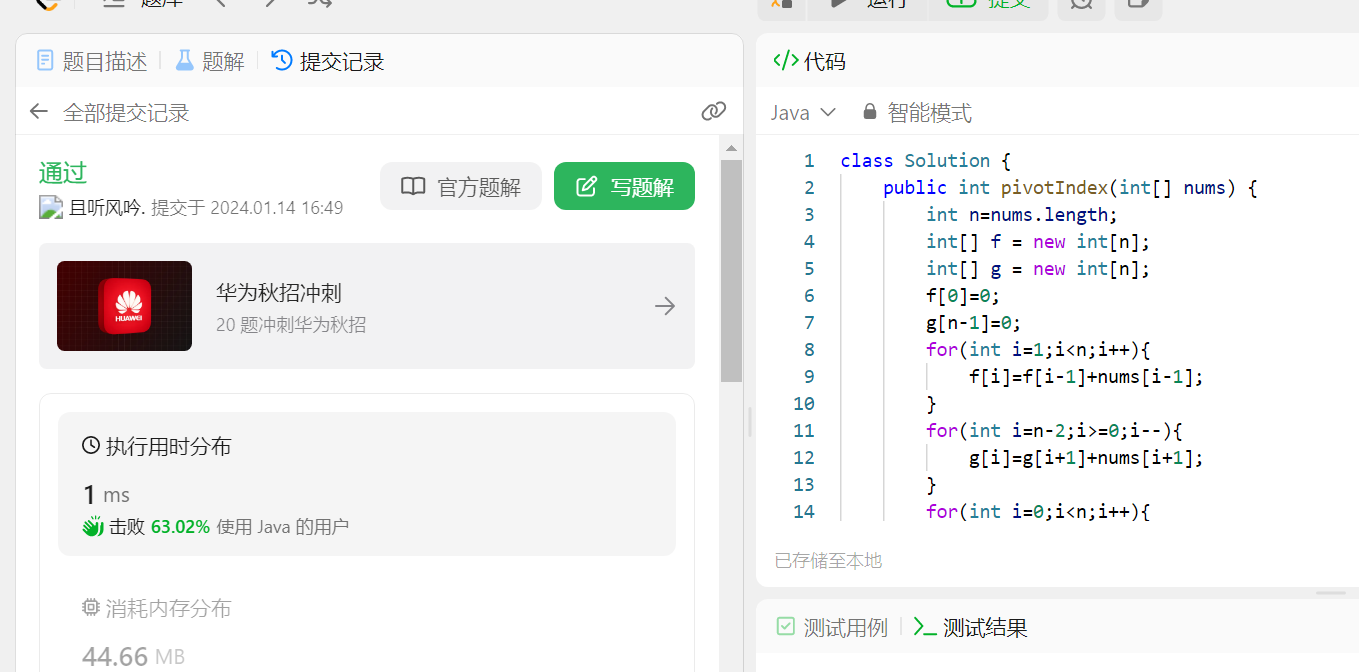
238.除自身以外数组的乘积

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = 1;
        g[n-1] = 1;
        for(int i=1;i<n;i++){
            f[i] = f[i-1] * nums[i-1];
        } 
        for(int i=n-2;i>=0;i--){
            g[i] = g[i+1] * nums[i+1];
        }
        int[] ret = new int[n];
        for(int i=0;i<n;i++){
            ret[i] = f[i] * g[i];
        }
        return ret;
    }
}