最优化总结

引入问题

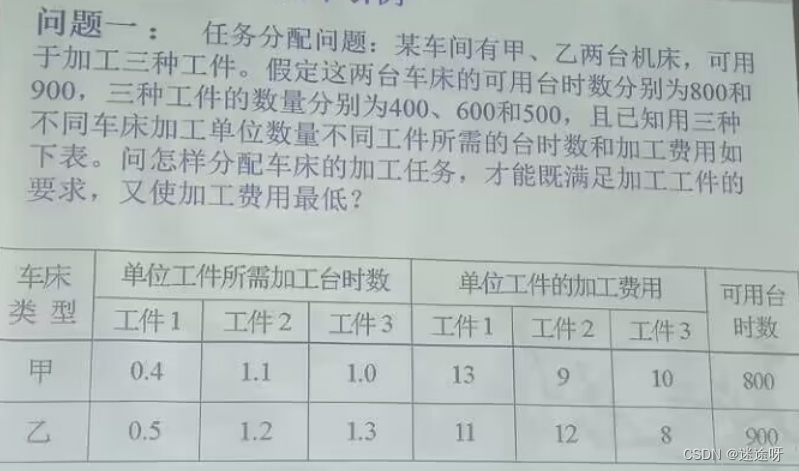
例1 运输问题

例2 生产计划问题

例3 指派问题

例4 数据拟合问题

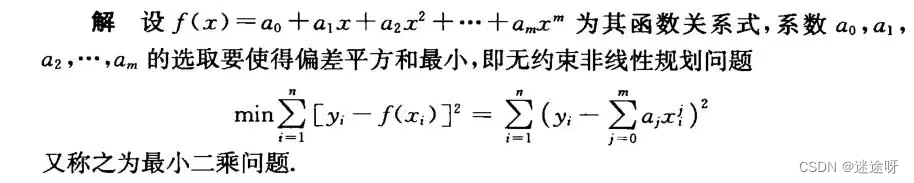
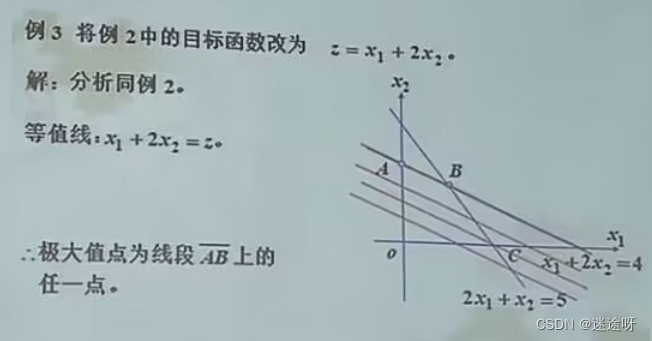
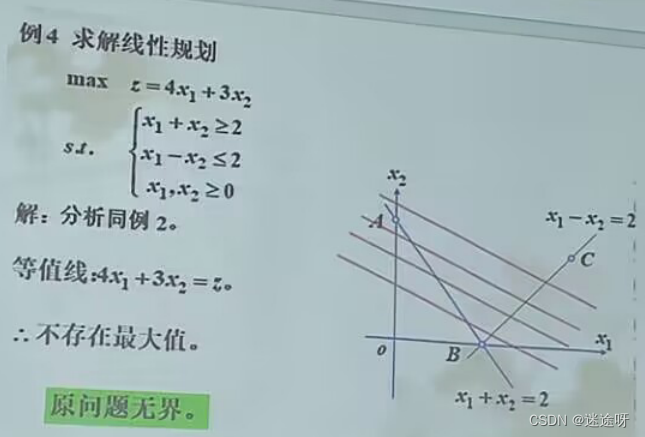
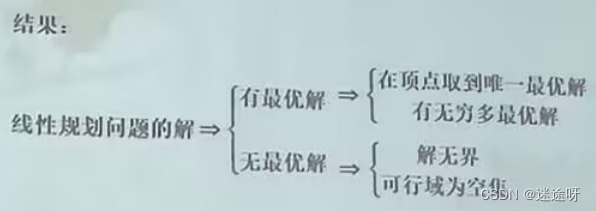
线性规划

向量和矩阵范数

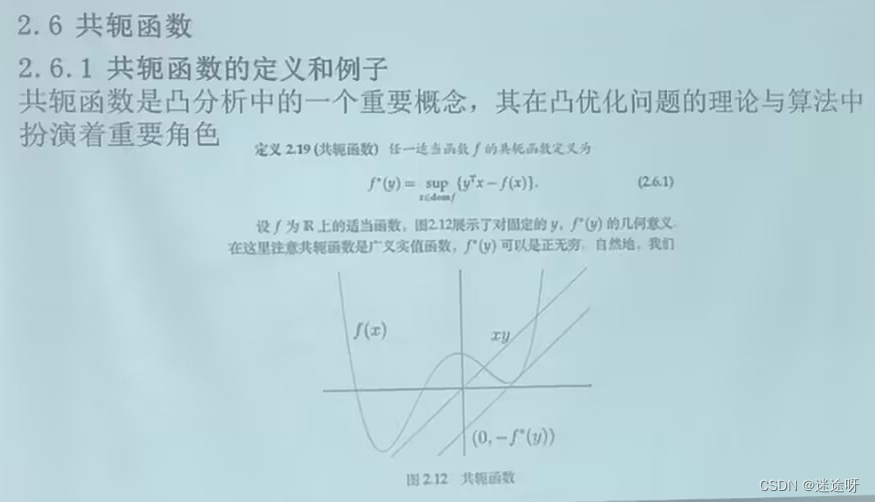
拟合

线性拟合

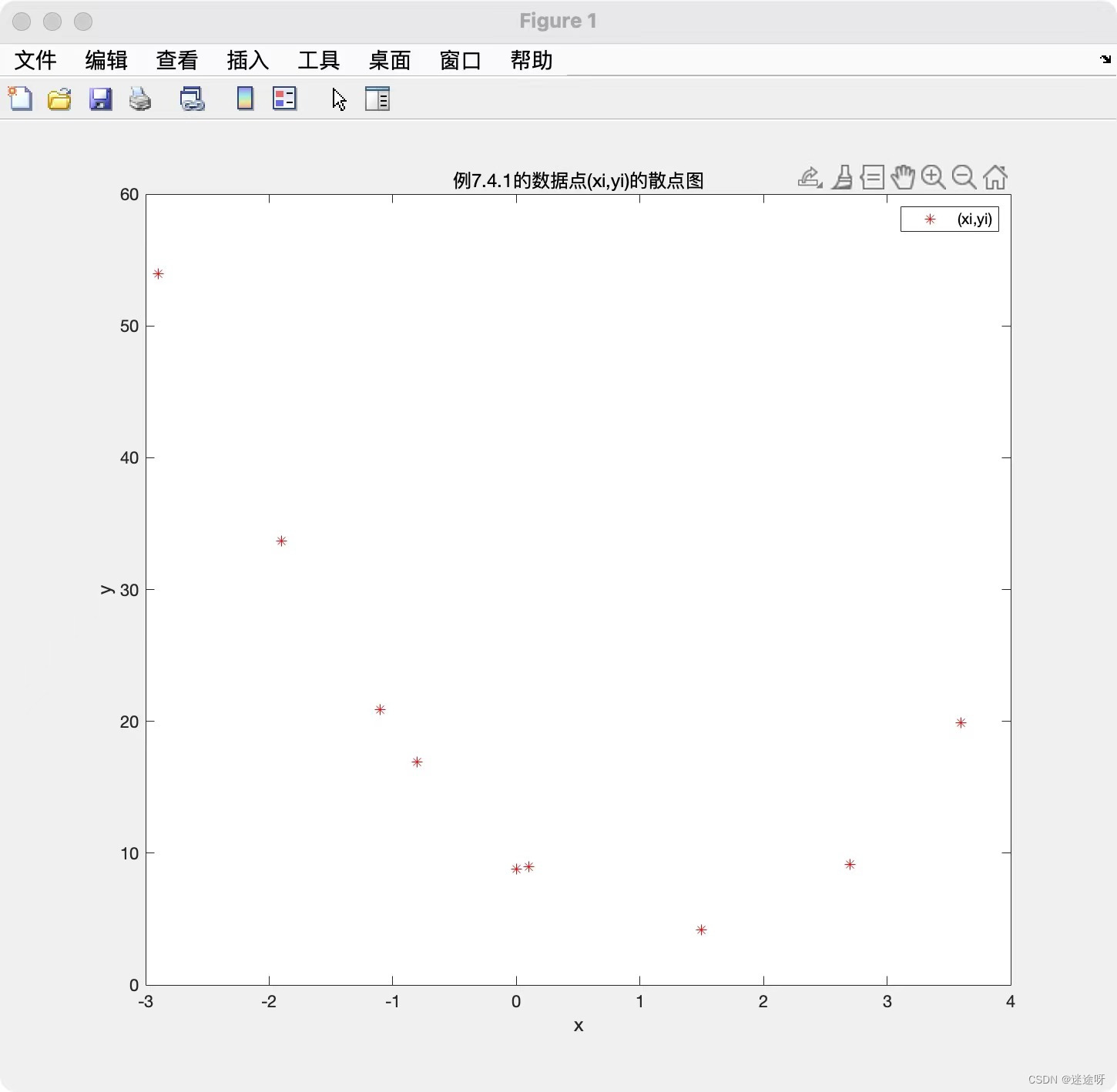
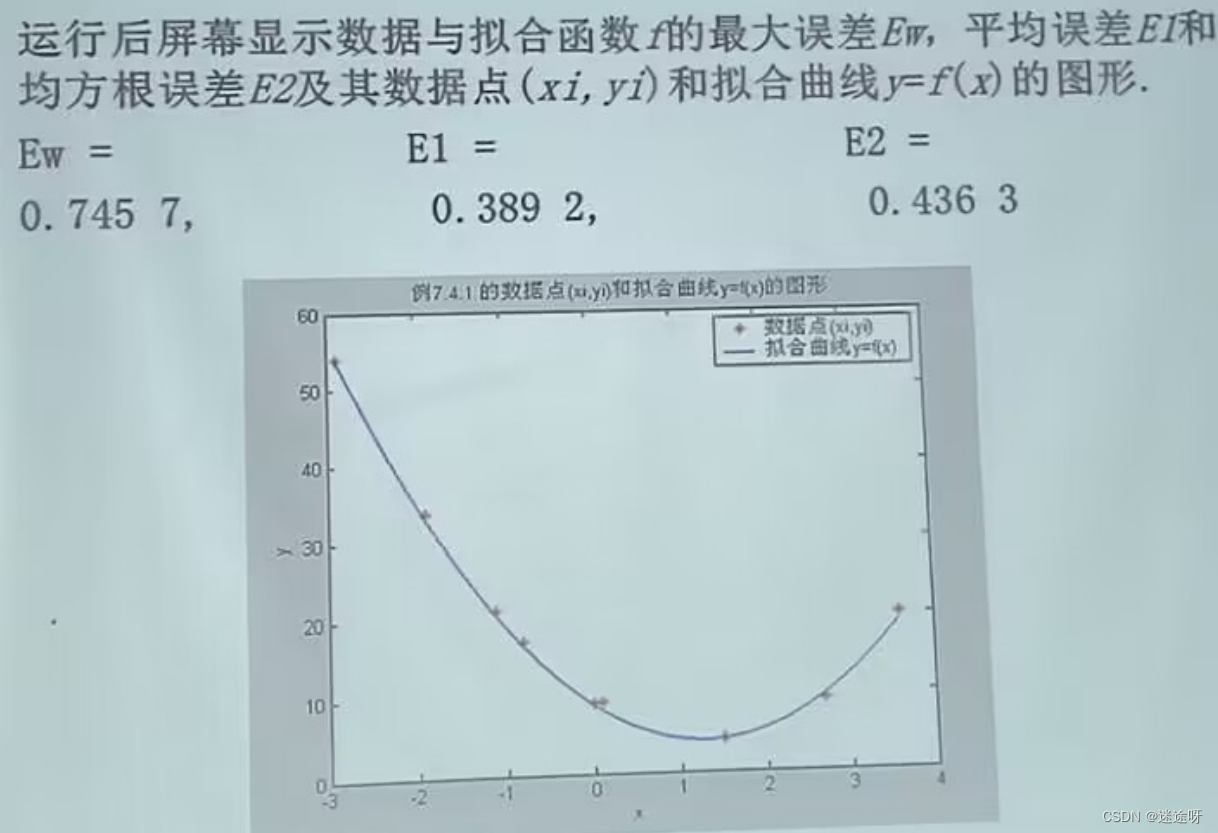
非线性拟合

无约束最优化问题的基本思想

实验

plot函数

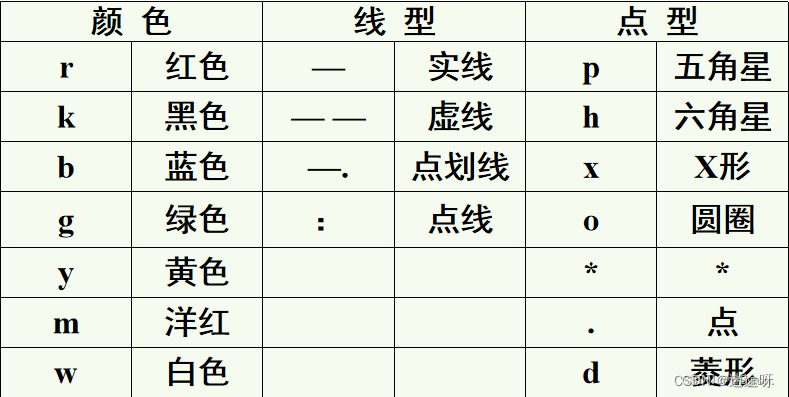
meshgrid函数

1. 用两个坐标轴上的点在平面上画格。
   用法：
   　　[X,Y]=meshgrid(x,y)
   　　[X,Y]=meshgrid(x)与[X,Y]=meshgrid(x,x)是等同的
   　　[X,Y,Z]=meshgrid(x,y,z)生成三维数组，可用来计算三变量的函数和绘制三维立体图
   　　
   　　例题1：

　　x=-3:1:3;
　　y=-2:1:2;
　　[X,Y]= meshgrid(x,y);

这里meshigrid（x，y）的作用是产生一个以向量x为行，向量y为列的矩阵，而x是从-3开始到3，每间隔1记下一个数据，并把这些数据集成矩阵X；同理y则是从-2到2，每间隔1记下一个数据，并集成矩阵Y。即

　　X=
　　-3 -2 -1 0 1 2 3
　　-3 -2 -1 0 1 2 3
　　-3 -2 -1 0 1 2 3
　　-3 -2 -1 0 1 2 3
　　-3 -2 -1 0 1 2 3
　　Y =
　　-2 -2 -2 -2 -2 -2 -2
　　-1 -1 -1 -1 -1 -1 -1
　　0 0 0 0 0 0 0
　　1 1 1 1 1 1 1
　　2 2 2 2 2 2 2

附注：例题中meshgrid(-3:1:3,-2:1:2);因为-3:1:3产生的是含有7个数字的行向量；-2:1:2产生的是含有5个数字的行向量。所以该命令的结果是产生57的矩阵（X,Y都是57的矩阵；其中X是由第一个含7个元素的行向量产生，Y是由第二个行向量产生）

2. meshgrid是MATLAB中用于生成网格采样点的函数。在使用MATLAB进行3-D图形绘制方面有着广泛的应用。
   生成绘制3-D图形所需的网格数据。在计算机中进行绘图操作时，往往需要一些采样点，然后根据这些采样点来绘制出整个图形。在进行3-D绘图操作时，涉及到x、y、z三组数据，而x、y这两组数据可以看做是在Oxy平面内对坐标进行采样得到的坐标对(x,y)。
   语法：
   　　[X,Y] = meshgrid(x,y)

上面的描述，我们可以知道，meshgrid返回的两个矩阵X、Y必定是行数、列数相等的，且X、Y的行数都等

于输入参数y中元素的总个数，X、Y的列数都等于输入参数x中元素总个数（这个结论可以通过查看meshgrid的源代码得到，可以通过示例程序得到验证）。

[X,Y]=meshgrid(x)与[X,Y]=meshgrid(x,x)是等同的
[X,Y,Z]=meshgrid(x,y,z)生成三维数组，可用来计算三变量的函数和绘制三维立体图

linprog函数

min f’x
约束条件： Ax<=b
等式约束条件： Aeqx=beq
lb<=x<=ub

linprog函数的调用格式如下：
linprog中f都是求最小值，这个要记住。 A和b是不等式约束条件的参数。 Aeq和beq是等式约束条件的参数。 lb和ub为x取值的取值范围。

函数使用形式：

x=linprog(f,A,b)  
x=linprog(f,A,b,Aeq,beq)  
x=linprog(f,A,b,Aeq,beq,lb,ub)  
x=linprog(f,A,b,Aeq,beq,lb,ub,x0)  
x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)  
[x,fval]=linprog(…)  
[x, fval, exitflag]=linprog(…)  
[x, fval, exitflag, output]=linprog(…)  
[x, fval, exitflag, output, lambda]=linprog(…)  

一般主要用的是：

x=linprog(f,A,b,Aep,beq,lb,ub);  

设定中主要要注意的就是参数的维数是否于使用的相对应。

举个例子吧：

例2：
生活中最常用的：假如有三种商品，a，b，c。三种商品总的数量不能超过30；c种商品不能超过15，b种商品不能超过10。
商品的单价是10,20,30。现在求三种商品各是多少，销售额最高。

转化为数学问题：

条件：
a+b+c<30
c<15
b<10

函数：

f = 10*a+20*b+30*c

因为linprog求的是最小值，一次我们改为：

f = -（10*a+20*b+30*c）

这样我们有了函数，然后根据约束条件不等式，有：

A = [1 1 1;0 0 1;0 1 0]  
b = [30 15 10]  

但这样算出来的结果大家会发现是小数，也可能是负数。

因此我们加入a b c取值的上下限

lb = [0 0 0]  
ub = [30 30 30]  

如果在计算中需要得到小数的结果，只要写成0.00或者30.00就可以了
最后带入函数计算即可。

原创内容，笔者才疏学浅，若有错误或遗漏之处，还望海涵，敬请指正，如有转载，请注明出处，谢谢！！！