【软件测试】路径覆盖

题目要求：

a)???????流程图如下：

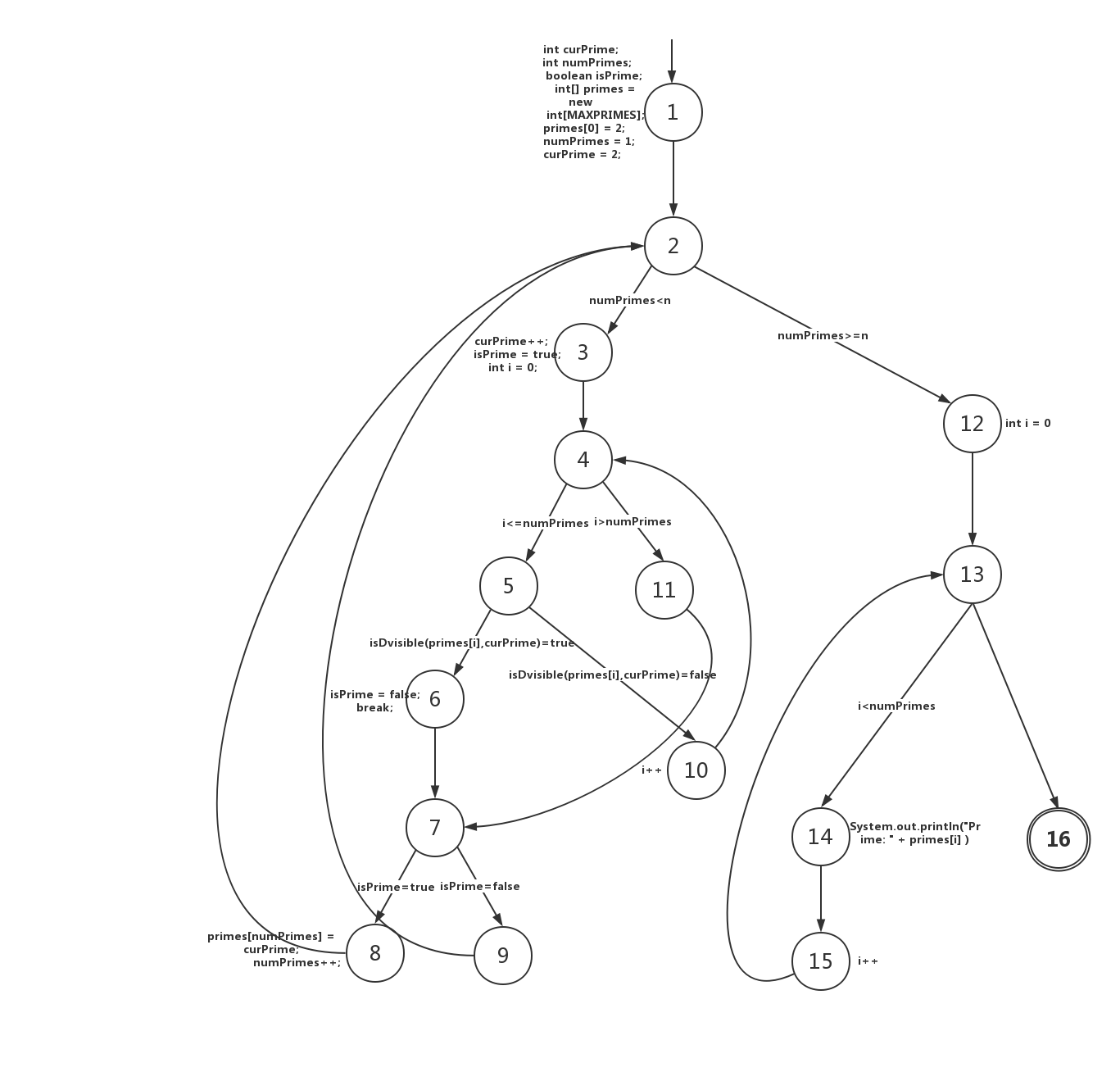
b) ? ?Consider test cases ti = (n = 3) and t2 = ( n = 5). Although these tour the same prime paths in printPrime(), they don't necessarily find the same faults. Design a simple fault that t2 would be more likely to discover than t1 would

Answer:如果将MAXPRIMES的值设为4那么n=5时可能会出现数组越界的错误。

c) ? ?For printPrime(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement to the for statement without going through the body of the while loop.

Answer:将n的值设为1

d) ? ?Enumerate the test requirements for node coverage, edge coverage,and prime path coverage for the path for printPrimes().

Answer:

点覆盖： {1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}

边覆盖：{{1,2}，{2,3}，{2,12}，{3,4}，{4,5}，{4,11}，{5,6}，{5,10}，{6,7}，{7,8}，{7,9}，{8,2}，{9,2}，{10,4}，{11，7}，{12,13}，{13,14}，{13,16}，{14，15}，{15,13}}

主路径覆盖:

{{1,2,3,4,5,6,7,8},

{1,2,3,4,5,6,7,9},

{1,2,3,4,5,10},

{1,2,3,4,11,7,8},

{1.2.3.4.11.7.9},

{1,2,12,13,14,15},

{1,2,12,13,16},

{2,3,4,5,6,7,8,2},

{2,3,4,5,6,7,9,2},

{2,3,4,11,7,8,2},

{2,3,4,11,7,9,2},

{3,4,5,6,7,8,2,12,13,14,15},

{3,4,5,6,7,8,2,12,13,16},

{3,4,5,6,7,9,2,12,13,14,15},

{3,4,5,6,7,9,2,12,13,16},

{4,5,10,4},

{4,5,6,7,8,2,3,4},

{4,5,6,7,9,2,3,4},

{4,11,7,8,2,3,4},

{4,11,7,9,2,3,4},

{5,10,4,5},

{5,6,7,8,2,3,4,5},

{5,6,7,9,2,3,4,5},

{6,7,8,2,3,4,5,6},

{6,7,9,2,3,4,5,6},

{7,8,2,3,4,5,6,7},

{7,9,2,3,4,5,6,7},

{7,8,2,3,4,11,7},

{7,9,2,3,4,11,7},

{8,2,3,4,5,6,7,8},

{8,2,3,4,11,7,8},

{9,2,3,4,5,6,7,9},

{9,2,3,4,11,7,9},

{10,4,5,10},

{11,7,8,2,3,4,11},

{11,7,9,2,3,4,11},

{13,14,15,13},

{14,15,13,14},

{15,13,14,15},

}

}

测试代码如下：

?

测试结果及覆盖路径：?

?

总结：

感谢每一个认真阅读我文章的人！！！

作为一位过来人也是希望大家少走一些弯路，如果你不想再体验一次学习时找不到资料，没人解答问题，坚持几天便放弃的感受的话，在这里我给大家分享一些自动化测试的学习资源，希望能给你前进的路上带来帮助

软件测试面试文档

我们学习必然是为了找到高薪的工作，下面这些面试题是来自阿里、腾讯、字节等一线互联网大厂最新的面试资料，并且有字节大佬给出了权威的解答，刷完这一套面试资料相信大家都能找到满意的工作

?