粒子滤波：Python实现

粒子滤波：Python实现

粒子滤波（Particle Filter）是一种基于蒙特卡罗方法的滤波技术，用于非线性、非高斯系统的状态估计。上期叙述了粒子滤波的理论与公式。本文将分析粒子滤波的实现过程，并通过一个简单的一维非线性系统的例子来展示其应用。

粒子滤波原理

1. 非线性系统模型

首先，我们定义了一个简单的非线性系统模型，具体形式为：

$$\begin{array}{c}{x}_k=0.5?x_{k?1}+\frac{25?x_{k?1}}{1+x_{k?1}^2}+8?\cos (1.2?u_k)+{?}_k\end{array}\text{\hspace{1em}?}$$
其中，$x_k$) 是系统在时刻 $k$的状态，$u_k$是输入，${?}_k$ 是系统噪声。

2. 粒子滤波函数

粒子滤波通过一组粒子来近似系统状态的概率分布。在我们的例子中，粒子滤波函数的主要步骤包括：

• 状态预测： 根据系统模型对每个粒子进行状态预测。
• 权重更新： 根据观测值，计算每个粒子的权重。
• 归一化权重： 保持权重的总和为1，进行权重的归一化。
• 重采样： 根据权重对粒子进行有放回或无放回的重采样。
• 估计结果： 通过加权平均得到最终的状态估计。

3. 应用于一维非线性系统

我们将粒子滤波应用于一个一维非线性系统，通过生成真实状态和带有噪声的观测数据，然后利用粒子滤波来估计系统的状态。通过调整粒子数量和初始状态猜测，我们可以观察粒子滤波在估计过程中的表现。

代码实现与结果展示

下面是通过 Python 实现的粒子滤波代码：

# @copyright all reseved
# @author: Persist_Zhang
import numpy as np
import matplotlib.pyplot as plt

# 定义非线性系统模型
def nonlinear_system_model(x, u):
    # 这里以一个简单的非线性系统为例，可以根据实际情况修改
    return 0.5 * x + 25 * x / (1 + x**2) + 8 * np.cos(1.2 * u)

# 粒子滤波函数
def particle_filter(num_particles, measurements, initial_state):
    particles = np.random.randn(num_particles) + initial_state
    weights = np.ones(num_particles) / num_particles

    estimated_states = []

    for measurement in measurements:
        # 递推状态预测
        particles = nonlinear_system_model(particles, 1) + 0.1 * np.random.randn(num_particles)

        # 权重更新
        likelihood = np.exp(-0.5 * (particles - measurement)**2)
        weights *= likelihood / np.sum(likelihood)

        # 归一化权重
        weights /= np.sum(weights)

        # 重采样
        indices = np.random.choice(np.arange(num_particles), size=num_particles, replace=True, p=weights)
        particles = particles[indices]

        # 估计结果
        estimated_state = np.sum(weights * particles)
        estimated_states.append(estimated_state)

    return estimated_states

# 生成真实状态数据
np.random.seed(42)
true_states = []
for _ in range(100):
    true_states.append(nonlinear_system_model(true_states[-1] if true_states else 0, 1) + 0.1 * np.random.randn())

# 生成观测数据
measurements = true_states + 0.5 * np.random.randn(100)

# 初始化粒子滤波
num_particles = 1000
initial_state_guess = 0
estimated_states = particle_filter(num_particles, measurements, initial_state_guess)

# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(true_states, label='True States', color='blue')
plt.scatter(range(len(measurements)), measurements, label='Measurements', color='red', marker='x')
plt.plot(estimated_states, label='Particle Filter Estimate', color='green')
plt.legend()
plt.xlabel('Time')
plt.ylabel('State')
plt.title('Particle Filter for Nonlinear System')
plt.savefig('./ParticleFilterng')
plt.show()

```![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/e938dd64438c4cabae29caf26b08a17c.png#pic_center)


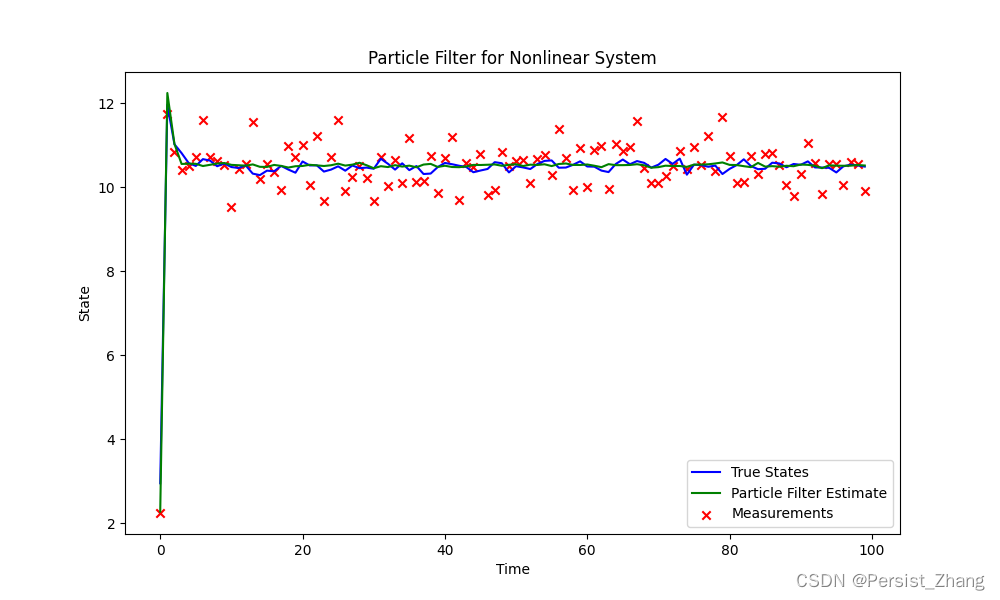
通过运行上述代码，我们可以观察到真实状态、观测数据以及粒子滤波的估计结果。这张图展示了粒子滤波在非线性系统中的应用，它通过考虑不确定性和噪声，对系统状态进行了有效的估计。

## 结论

粒子滤波作为一种非参数化、适用于非线性系统的滤波方法，为处理实际应用中的复杂问题提供了有力的工具。通过合理设置粒子数量和初始条件，粒子滤波可以在非线性系统中提供较为准确的状态估计。然而，也需要注意到其计算复杂度随粒子数量增加而增加的特点，因此在实际应用中需要权衡计算资源和精度。