LeetCode 160: 两个链表的相交节点 - 优雅解法
LeetCode 160: Intersection of Two Linked Lists
题目描述
给定两个单链表 headA 和 headB 的头节点,返回它们相交的节点。如果两个链表没有相交,返回 null。
示例:
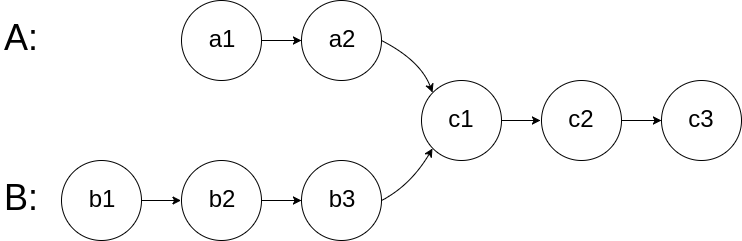
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:相交节点 '8'
解释:链表A和链表B在节点 '8' 相交。
解题思路
为了解决这个问题,我们可以分三个步骤进行:
- 计算两个链表的长度。
- 通过指针操作,使得两个链表的起点到相交节点的距离相等。
- 同时遍历两个链表,找到第一个相同的节点即为相交节点。
解题方法
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == headB) {
return headA;
}
int lenA = 0, lenB = 0;
// 计算链表长度
while (headA != null) {
lenA++;
headA = headA.next;
}
while (headB != null) {
lenB++;
headB = headB.next;
}
// 重新指向链表头
headA = headA;
headB = headB;
// 使两链表起点到相交节点的距离相等
while (lenA > lenB) {
headA = headA.next;
lenA--;
}
while (lenB > lenA) {
headB = headB.next;
lenB--;
}
// 同时遍历,找到相交节点
while (headA != null && headB != null) {
if (headA == headB) {
return headA;
}
headA = headA.next;
headB = headB.next;
}
return null;
}
}
复杂度
时间复杂度: O ( m + n ) O(m + n) O(m+n),其中 m m m 和 n n n 分别为两个链表的长度。
空间复杂度: O ( 1 ) O(1) O(1),未使用额外空间。
优化解法
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA = headA;
ListNode pB = headB;
while (pA != pB) {
pA = (pA == null) ? headB : pA.next;
pB = (pB == null) ? headA : pB.next;
}
return pA;
}
}
在优化解法中,我们使用两个指针(pA 和 pB)来遍历两个链表。当其中一个指针到达链表末尾时,我们将其重定向到另一个链表的头部。这确保两个指针同时覆盖两个链表的总长度。最终,它们将在相交点相遇或到达链表末尾(null)。这种方法避免了计算链表长度,减少了冗余操作。
这个优化解法的时间复杂度是 O ( m + n ) O(m + n) O(m+n),空间复杂度是 O ( 1 ) O(1) O(1),是一种更为优雅的实现。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 安装 yarn、pnpm、功能比较
- 《SPSS统计学基础与实证研究应用精解》视频讲解:SPSS数据查找
- Vue组件provide,inject的代码及总结
- GEM5 McPAT教程:源代码解读McPAT NoC功耗 arbiter部分
- 通过WebSocket实现异步导出
- ArduPilot之开源代码电压/电流校准
- 阿里云服务器固定带宽下载和上传速度对照表
- 计算机毕业设计-----ssm+mysql实现的JavaWeb酒店管理系统
- 【95 6K?】Scrcpy:一款免费、强大且实用的Android镜像投屏控制软件
- Linux基础第七章:磁盘阵列(RAID)