Python机器学习 – 用最小二乘法实现散点图

发布时间：2023年12月24日

Python机器学习 – 用最小二乘法实现散点图

Machine Learning in Python – Implement Scatter Plot with Least Squares

By Jackson@ML

1. 最小二乘法定义

最小二乘法是由A.M.Legendre（勒让德）先生最早提出的。他在1805年，通过《计算彗星轨道的新方法》提出最小二乘法。它的主要思想是通过求解模型未知参数，使模型的理论值和观察值之差的平方和达到最小。

在散点图中，如果散点大致分布在观测直线的附近，则称两个变量（x, y）之间具有线性相关性。那么，这条直线就叫做回归直线，该直线方程为：观察值y = wx + b

由于这条直线满足所有样本点到这条直线的距离最小，因此，选择点到直线的垂直距离来表示各点与直线的最小距离的偏差。

最小二乘法公式是一个数学的公式，在数学上称为曲线拟合，不仅包括线性回归方程，还包括矩阵的最小二乘法。

2. 线性回归算法示例

最小二乘法属于线性回归算法的一种。以下给出Python代码来体现具体示例。
假设货运量和工业总产值都有一组数据，现在要求求出工业总产值与货运量之间的函数关系。

程序需要先行安装matplotlib库，在命令行窗口(cmd)或者Power Shell终端使用以下命令：

pip install matplotlib

安装完毕后，导入matplotlib库，然后将两组数据分别存储到x, y两个列表中，再画出散点图。
代码如下所示：

import matplotlib.pyplot as plt

x = [2.8, 2.9, 3.2, 3.2, 3.4, 3.2, 3.3, 3.7, 3.9, 4.2, 3.9, 4.1, 4.2, 4.4, 4.2]
y = [25, 27, 29, 32, 34, 36, 35, 39, 42, 45, 44, 44, 45, 48, 47]

plt.scatter(x, y)
plt.show()

执行结果如下图所示：
在这里插入图片描述

3. 最小二乘法示例

接下来，定义函数avg(x), 这个函数的功能是求解平均数。函数avg传递参数x，返回的平均值等于求和除以样本数。

最后，定义拟合函数fit(x, y), 返回变量w和b。并且调用拟合函数fit(x, y), 形成预测y值列表，并绘制最终带观测直线的散点图。

完整代码如下：

import matplotlib.pyplot as plt

x = [2.8, 2.9, 3.2, 3.2, 3.4, 3.2, 3.3, 3.7, 3.9, 4.2, 3.9, 4.1, 4.2, 4.4, 4.2]
y = [25, 27, 29, 32, 34, 36, 35, 39, 42, 45, 44, 44, 45, 48, 47]

plt.scatter(x, y)
plt.show()

def avg(x):
    m = len(x)
    sum = 0
    for num in x:
        sum += num 
    return sum / m 

def fit(x, y):
    x_avg = avg(x)
    y_avg = avg(y)
    m = len(x)
    tmp_1 = 0; tmp_2 = 0
    for i in range(m):
        tmp_1 += (x[i] - x_avg) * (y[i] - y_avg)
        tmp_2 += (x[i] - x_avg) ** 2
    w = tmp_1 / tmp_2
    b = y_avg - w * x_avg
    return w, b 

w, b = fit(x, y)
print(w)
print(b)

pre_y = []
for i in range(len(y)):
    pre_y.append(w * x[i] + b)
    
plt.scatter(x, y)
plt.plot(x, pre_y, c='r')
plt.show()

运行该程序，显示下图结果：
在这里插入图片描述
退出该图后，会显示出另一幅带观测直线的散点图，如下图所示：

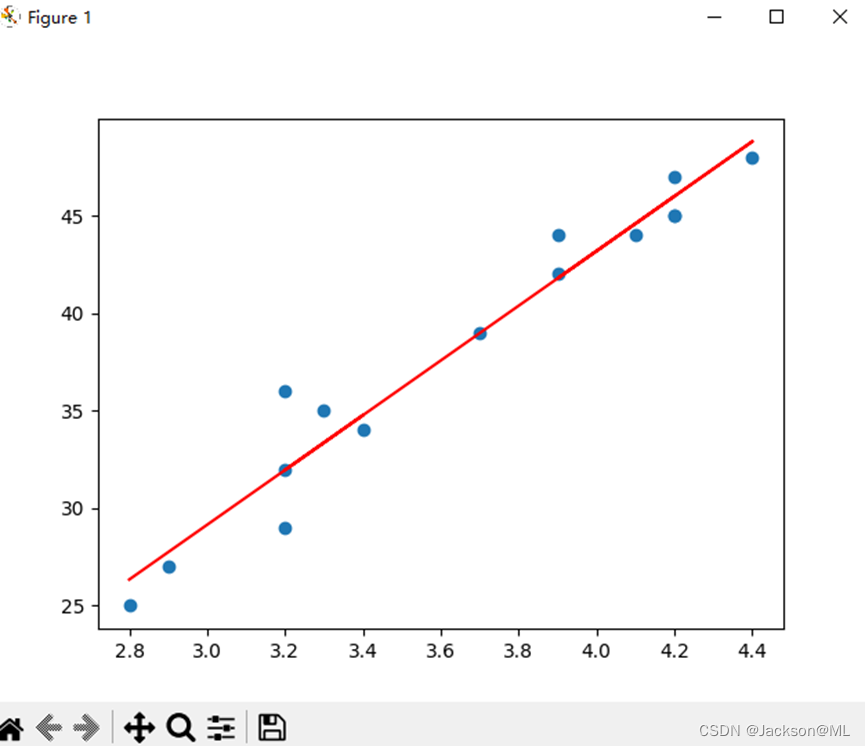
这正是我们想要的结果！

在以上程序中，m为样本容量，即实验次数；x, y为任意一组实验的观测值。

4. 小结：

本文简要介绍了最小二乘法上机实训的过程。通过最小二乘法的实践，用Python外带的matplotlib库实现了散点图及其观测直线。

该程序实现的主要步骤如下：
1）首先定义avg(x)函数，返回x样本数据的平均数；
2）其次，拟合函数fit(x, y)通过调用avg()函数求解x的平均值和y的平均值；同时，求解x的长度，即实验次数。
3）在初始化tmp_1, tmp_2的值为零后，构建最小二乘法w公式的分子和分母；然后，求解w, b的值并返回。
4）接下来，初始化预测y值的列表为空，遍历所有元素并求解预测y值，将其添加到预测y值列表。最后，分别绘制观测直线并绘制散点图。

以上是用Python实现最小二乘法的过程，希望对读者有所帮助。

参考文献

《机器学习技术及应用》（徐宏英等著）一书的监督学习的相关内容，谨此表示感谢。

Python机器学习 – 用最小二乘法实现散点图