算法复习——01背包

01背包

DP分析法要素有：集合，属性，状态计算
（集合是指只考虑前i个，总体积小于等于j的所有选法，存取的属性是所有选法的最大值）

状态方程计算（所有选法可以分为2种不同的子集）

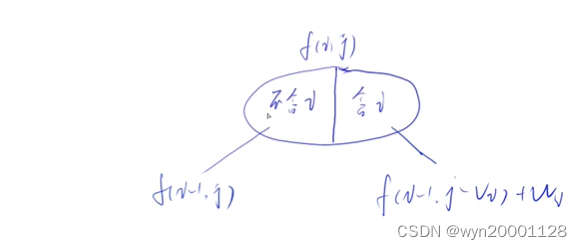
左边子集的属性：不含有第i个物品，所以表示为$f（i?1，j）$
右边子集的属性：含有第i个物品（间接计算一下），
表示为$f（i?1，j?v[i]）+w_j$
则$f（i，j）的属性是上述二者的最大值$
代码如下：

#include <iostream>
#include <algorithm>
using namespace std;
int v[1010];
int w[1010];
int dp[1010][1010];
int main ()
{
    int i,j,n,m;
    cin>>n>>m;
    for(i=1;i<=n;i++)  cin>>v[i]>>w[i];//输入容积和价值
    for(i=1;i<=n;i++)//此时dp[0][j]一定是0
    {
        for(j=0;j<=m;j++)
        {
            if(j>=v[i]) dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);//特判j大于v[i]的情况
            else dp[i][j]=dp[i-1][j];
        }
    }
    cout<<dp[n][m]<<endl;
    return 0;
}

ps：真正的初始化代码（只考虑前1个）应该是

for(j=1;j<=m;j++)
{
     if(j>=v[1]) dp[1][j]=w[1];
     else dp[1][j]=0;
}

而后i从2再开始进行状态计算，上述代码可以等价这个初始化代码，其他DP的题目的时候要注意DP的初始化。