代码随想Day39 | 62.不同路径、63. 不同路径 II
发布时间:2023年12月18日
62.不同路径?
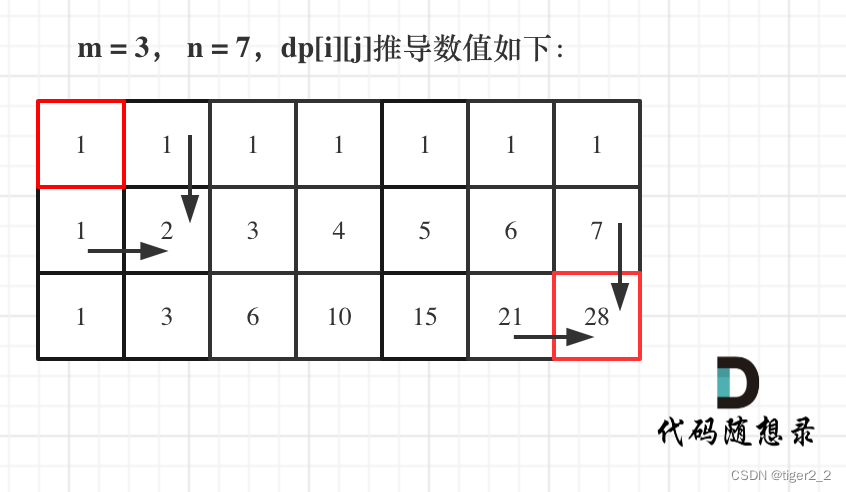
每次向右或者向下走两个选择,定义dp数组dp[i][j] 为到达索引ij的路径和,状态转移公式为
dp[i][j]=dp[i-1][j]+dp[i][j-1],初始状态的第一行和第一列为1,从左上到右下开始遍历即可。详细代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>>dp (m,vector<int>(n,1));
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};为了优化空间复杂度,可以用一个一维数组,因为一定是先更新左边的值再更新右边的值。
详细代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int>dp (n,1);
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[j]+=dp[j-1]; //当前dp为从上方路径来,dp[j-1]为从左方来
}
}
return dp[n-1];
}
};63.?不同路径?II?
这道题和上一道思路一样,但是这道有障碍物,需要注意有障碍物的索引,到达该处的路径和为0,根据这个条件,增加处理逻辑即可,整体的转移方程还是
详细代码如下:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty()) return 0;
vector<vector<int>>dp(obstacleGrid.size(),vector<int>(obstacleGrid[0].size(),0));
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
for(int i=0;i<m;i++)
{
if(obstacleGrid[i][0]==1||i>0&&dp[i-1][0]==0) dp[i][0]=0;
else dp[i][0] = 1;
}
for(int j=1;j<n;j++)
{
if(obstacleGrid[0][j]==1||dp[0][j-1]==0) dp[0][j]=0;
else dp[0][j] = 1;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
if(obstacleGrid[i][j]==1) dp[i][j]=0;
else dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};感觉这道题的优化空间版本细节有点多,但还是附上代码:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty()) return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<int>dp (n,0);
for(int j=0;j<n;j++)
{
if(obstacleGrid[0][j]==1||j>0&&dp[j-1]==0) dp[j]=0;
else dp[j] = 1;
}
for(int i=1;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(obstacleGrid[i][j]==1) dp[j]=0;
else if(j>0) dp[j] = dp[j]+dp[j-1];
}
}
return dp[n-1];
}
};
文章来源:https://blog.csdn.net/juantingliu_01/article/details/135051246
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 本地安装运行LLM(大型语言模型)
- java中HashMap的七种遍历方式
- 数据结构:队列
- 详解ISIS动态路由协议
- C语言—每日选择题—Day42
- C++单例设计模式
- Ascend C算子开发常见问题案例
- C语言学习NO.9-指针(一)内存和地址,指针变量,指针变类型的意义,const修饰指针,指针运算,野指针,assret断言,指针的使用和传址调用
- test mock-05-mockserver mock-server/hoverfly/wiremock 对比
- 第十三章 : Spring Cloud Alibaba Sentinel熔断和限流实战