【机器学习】西瓜书第6章支持向量机课后习题6.1参考答案

【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机

1.试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)。

首先，直观解释二维空间内点到直线的距离：

由平面向量的有关知识，可得：

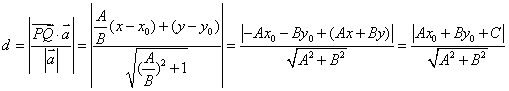
超平面的法向量为 $w$，任取平面上一点$x_0$，则超平面可以表示为${\omega }^T?x_0+b=0$。一个点 $x$到超平面的距离可以用该点到 $x_0$ 的距离在法向量 (ω) 方向上的投影来表示，即：

$$\text{距离}=\frac{|{\omega }^T(x?x_0)|}{||\omega ||}=\frac{|{\omega }^{T}x+b|}{||\omega ||}$$
其中：

• ${\omega }^T$ 表示向量 $w$ 的转置。
• $||\omega ||$ 表示向量 $w$ 的范数（模长）。
• $x$ 是指向平面上的任意点。
• $x_0$ 是平面上的某一点。
• $b$ 是平面的偏置项。

这个公式表示了点 $x$ 到平面的距离，计算方式是将点 $x$ 投影到法向量 $\omega$ 上，然后除以 $\omega$ 的模长。

其中 ω = ( ω_1; ω_2; … ; ωd) 为法向量，决定了超平面的方向 ; $b$ 为位移项，决定
了超平面与原点之间的距离.