PSEUDO-LIDAR++：自动驾驶中 3D 目标检测的精确深度

论文地址：PSEUDO-LIDAR++: ACCURATE DEPTH FOR 3D OBJECT DETECTION IN AUTONOMOUS DRIVING
论文代码：https://github.com/mileyan/Pseudo_Lidar_V2

摘要

3D 检测汽车和行人等物体在自动驾驶中发挥着不可或缺的作用。现有方法很大程度上依赖昂贵的激光雷达传感器来获取准确的深度信息。虽然最近推出了伪激光雷达作为一种有前途的替代方案，但仅基于立体图像的成本要低得多，但仍然存在显着的性能差距。

论文通过立体深度估计的改进为伪激光雷达框架提供了实质性的进步。具体来说，论文调整立体网络架构和损失函数，使其与远处物体的准确深度估计更加一致——目前这是伪激光雷达的主要弱点。此外，探索利用更便宜但极其稀疏的 LiDAR 传感器来消除深度估计的偏差，这些传感器本身无法为 3D 检测提供足够的信息。
论文提出了一种深度传播算法，以初始深度估计为指导，将这几个精确的测量结果扩散到整个深度图上。

引言

自动驾驶汽车的安全驾驶需要对汽车、行人和其他目标进行精确的 3D 检测和定位。这反过来又需要准确的深度信息，这些信息可以从 LiDAR（光探测和测距）传感器获得。尽管 LiDAR 传感器高度精确且可靠，但其价格却非常昂贵：64 光束型号的成本约为 75,000 美元。另一种方法是通过廉价的商用相机测量深度。
然而，尽管伪 LiDAR 最近在基于立体（双目相机）的 3D 目标检测方面取得了巨大进展 [1]，仍然存在显着的性能差距，尤其是对于远处的物体（我们希望尽早检测到，以便有时间做出反应）。负担能力和安全性之间的权衡造成了道德困境。

[1] Yan Wang, Wei-Lun Chao, Divyansh Garg, Bharath Hariharan, Mark Campbell, and Kilian Q. Weinberger. Pseudo-lidar from visual depth estimation: Bridging the gap in 3d object detection for autonomous driving. In CVPR, 2019a.

本文中，结合了两个角度的见解，提出了解决这一剩余挑战的可能解决方案。观察到，与基于 LiDAR 的系统相比，基于立体系统的 3D 目标定位误差更高，完全源于深度估计中的更高误差（在获得 3D 点云之后，这两种方法是相同的。重要的是，这个错误不是随机 的，而是系统的：观察到立体方法确实能够以高可靠性检测目标，但它们估计整个目标的深度要么太远要么太近。

如图：绿色框是 KITTI 数据集中汽车的地面真实位置，红点是通过立体视差网络获得的。使用立体深度网络 (SDN) 获得的紫色点更接近事实。经过深度传播（蓝点）和一些（黄色）LiDAR 测量后，汽车正好位于绿色方框内。 （一层正方形为 1m × 1m），红色立体点捕获汽车，但完全偏离地面实况位置（绿色框）约 2m。
如果能够消除这些深度估计的偏差，即使对于远处的目标也应该能够获得准确的 3D 定位，而无需高昂的成本。

论文首先重新审视嵌入最先进的立体 3D 检测方法核心的深度估计例程。
系统深度偏差的一个主要因素来自于深度通常不直接计算的事实。相反，论文首先估计视差（左右图像之间像素的水平移位），然后将其反转以获得逐像素深度。

虽然深度神经网络的使用极大地改善了视差估计，但设计和学习网络以优化准确性由于相互变换，视差估计的方法只是过分强调附近的物体。
例如，5米远物体的单位视差误差（以像素为单位）意味着10厘米的深度误差：侧镜的长度。然而，对于 50 米外的物体，相同的视差误差会变成 5.8m 的深度误差：整辆车的长度。对这两个错误进行同等惩罚意味着网络花费更多的时间来纠正附近物体上的细微错误，而不是远处物体上的严重错误，从而导致深度估计降低，最终导致远处物体的检测和定位效果不佳。
提出因此，论文t采用立体网络架构和损失函数来进行直接深度估计。具体来说，融合左右图像的 cost volume 以及随后的 3D 卷积是立体网络中的关键组成部分。采用卷积的中心假设——所有邻域都可以以相同的方式进行操作——论文提出在深度网格而不是视差网格上构建成本量，从而使 3D 卷积和损失函数能够在深度估计的正确尺度上精确执行。论文的网络被称为立体深度网络（SDN）。

尽管 SDN 显着改进了深度估计，但立体图像本质上仍然是 2D，并且尚不清楚它们是否能够与真正的 3D LiDAR 传感器的准确性和可靠性相匹配。尽管具有 32 或 64 光束的 LiDAR 传感器价格昂贵，但仅具有 4 光束的 LiDAR 传感器便宜两个数量级2，因此很容易负担得起。4 束激光束非常稀疏，不适合单独捕获 3D 物体形状，但如果与立体图像配对，它们将成为消除密集立体深度估计偏差的理想工具：单个高精度激光束可以告诉我们如何校正整个汽车或行人在其路径中的深度。
为此，论文提出了一种新颖的深度传播算法，其灵感来自于基于图的流形学习。简而言之，通过最近邻图在本地连接估计的 3D 立体点云，这样对应于同一目标的点将彼此共享许多本地路径。首先将少数但精确的 LiDAR 测量值与像素（无论深度）进行匹配，然后与相应的 3D 点进行匹配，以获得图中多个节点的准确深度估计。最后，使用标签扩散机制沿图传播精确的深度信息，从而以可忽略的成本生成密集且准确的深度图。在上图中，看到少量（黄色）LiDAR 测量结果足以将整辆车的几乎所有最终（蓝色）点定位在绿色地面实况框中。

背景

3D 物体检测

大多数 3D 物体检测。工作都以 LiDAR 的 3D 点云为输入等人；Frustum PointNet 将 PointNet 直接应用于点，而 Voxelnet 将它们量化为 3D 网格。对于街道场景，一些研究发现处理鸟瞰图的点已经可以捕获物体的轮廓和位置。图像也被使用，但主要是为了补充 LiDAR。早期仅基于图像的工作主要建立在 2D 正面视图检测管道上——在 3D 目标定位方面远远落后。

伪点云

最近，随着 [1] 中提出的伪激光雷达框架的引入，这一差距已显着缩小。该框架采用了与之前基于图像的 3D 目标检测器截然不同的方法。伪激光雷达不是直接从场景的正面视图检测 3D 边界框，而是从基于图像的深度估计开始，预测每个图像像素 $(u,v)$ 的深度 $Z(u,v)$。然后将生成的深度图 $Z$ 反投影到 3D 点云中：像素 $(u,v)$ 将通过以下方式转换为 3D 中的 $(x,y,z)$：
$$z=Z(u,v),x=\frac{(x?c_U)\times z}{f_U},y=\frac{(v?c_V)\times z}{f_V},\text{\hspace{1em}(1)}$$

其中 $(c_U，c_V)$ 是相机中心，$f_U$ 和 $f_V$ 是水平和垂直焦距。然后，3D 点云将被完全视为 LiDAR 信号 - 任何基于 LiDAR 的 3D 探测器都可以无缝应用。

立体视差估计

伪激光雷达在很大程度上依赖于深度估计的质量。本质上，如果估计的像素深度与 LiDAR 提供的像素深度相匹配，则具有任何基于 LiDAR 的检测器的伪 LiDAR 应该能够实现与将相同检测器应用于 LiDAR 信号所获得的性能相同的性能。
根据立体图像对的深度估计用于 3D 目标检测比单目即单目图像更准确。因此，论文专注于立体深度估计，这通常是通过估计图像之间的视差获得的。

视差估计算法采用一对左右图像 $I_l$ 和 $I_r$ 作为输入，从一对具有水平偏移（即基线）$b$ 的相机捕获。不失一般性，假设该算法将左图像 $I_l$ 作为参考，并输出视差图 $D$，记录每个像素 $(u,v)$ 的水平视差 $I_r$ 。理想情况下，$I_l(u,v)$ 和 $I_r(u,v+D(u,v))$ 将描绘相同的 3D 位置。因此，可以通过以下变换导出深度图 $Z$，
$$Z(u,v)=\frac{f_U\times b}{D(u,v)}(f_U:\text{水平焦距}),\text{\hspace{1em}(2)}$$

视差估计的常见流程是首先构建 4D 视差 cost vloume $C_{disp}$，其中 $C_{disp}(u,v,d,:)$ 是一个特征向量，捕获 $I_l(u,v)$ 和 $I_r(u,v+d)$ 之间的像素差异。然后根据 cost vloume $C_{disp}$ 估计每个像素 $(u,v)$ 的视差 $D(u,v)$。一种基本算法是使用 $C_{disp}(u,v,d)=||(u,v)?I_r(u,v+d)|{|}_2$ 构建 3D cost vloume，并将 $D(u,v)$ 确定为 $argmi{n}_d{C}_{disp}(u,v,d)$。高级算法在构建 $C_{disp}$ 时利用更强大的功能，并对 $D$ 执行结构化预测。

PSMNet 首先从 $I_l$ 和 $I_r$ 中分别提取深度特征图 $h_l$ 和 $h_r$。然后它通过连接 $h_l(u,v)$ 和 $h_r(u,v+d)$ 的特征来构造 $C_{disp}(u,v,d,:)$，接下来是 3D 卷积层。 得到的 3D 张量 $S_{disp}$（特征通道大小最终为 1）随后用于通过以下加权组合导出像素视差：
$$D(u,v)=\sum _d\text{softmax}(?S_{disp}(u,v,d))\times d,\text{\hspace{1em}(3)}$$

其中，softmax 是沿着 $S_{disp}$ 的第三维执行的。 PSMNet 可以端到端学习，包括图像特征提取器和 3D 卷积核，以最小化视差误差:
$$\sum _{(u,v)\in \mathcal{A}}?(D(u,v)?D^{?}(u,v)),\text{\hspace{1em}(4)}$$

其中 $?$ 是平滑的 L1 损失，$D^{?}$ 是地面实况图，$\mathcal{A}$ 包含具有地面实况的像素。

立体深度网络 (SDN)

设计和学习以最小化视差误差（参见公式 4）的立体网络可能会过度强调具有较小深度的附近物体，因此在估计远处物体的深度时表现不佳。要了解这一点，请注意等式 2 意味着对于给定的视差 $\delta D$ 误差，深度 $\delta Z$ 误差随深度呈二次方增加：
$$Z\propto \frac{1}{D}?\delta Z\propto \frac{1}{D^2}\delta D?\delta Z\propto Z^2\delta D\text{\hspace{1em}(5)}$$

中间项是通过对 $Z(D)$ w.r.t. $D$ 进行微分获得的。 特别是，使用 KITTI 数据集上的设置，视差中的单个像素误差意味着在 5 米深度处仅存在 0.1m 的深度误差，而在 5 米深度处则存在 5.8m 的误差。深度50米。

如下图为从视差到深度的映射：

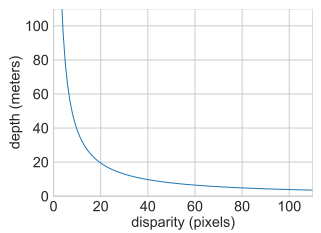
深度损失

论文提出了两项??改变来适应立体网络以进行直接深度估计。
首先，学习立体网络来直接优化深度损失
$$\sum _{(u,v)\in \mathcal{A}}?(Z(u,v)?Z^{?}(u,v)).\text{\hspace{1em}(6)}$$

$Z$ 和 $Z^{?}$ 可以使用公式 2 从 $D$ 和 $D^{?}$ 获得。从视差损失到深度损失的变化纠正了对附近物体微小深度误差的过分强调——必要但仍然不够克服视差估计的问题。

Depth Cost Volume

为了促进准确的深度学习（而不是视差），需要进一步解决深度估计管道的内部问题。错误的一个重要来源是 4D 视差 cost volume 内的 3D 卷积，其中相同的内核应用于整个 cost volume 。这是一个很大的问题，因为它隐含地假设卷积的效果在整个过程中是均匀的——这明显违反了深度与视差关系的倒数（图 2）。例如，局部平滑视差为 85 和 86 的两个相邻像素（将深度更改几厘米以平滑表面）可能是完全合适的，而对视差为 5 和 6 的两个像素应用相同的内核可以轻松移动 3D 点相差 10m 或更多。

考虑到这一见解和卷积的中心假设（所有邻域都可以以相同的方式进行操作），我们提出改为构造 Depth Cost Volume $C_{depth}$ ，其中 $C_{depth}(u,v,z,:)$ 将编码特征描述像素 $(u,v)$ 的深度 $Z(u,v)$ 为 $z$ 的可能性。随后的 3D 卷积将在深度网格（而不是视差）上运行，以相同的方式影响相邻深度，而与它们的位置无关。然后使用生成的 3D 张量 $S_{depth}$ 来预测像素深度，类似于公式 3
$$Z(u,v)=\sum _{z}softmax(?S_{depth(u,v,z)})\times z.$$

论文基于这样的直觉构造新的深度体积 $C_{depth}$：$C_{depth}(u,v,z,:)$ 和 $C_{disp}(u,v,\frac{f_U\times b}{z},:)$， 应该导致等效的 “cost”。
为此，应用双线性插值，使用等式 2 中的深度到视差变换从 $C_{disp}$ 构造 $C_{d}epth$。具体来说，考虑 PSMNet 后 [0, 191] 范围内的视差，并考虑[1m,80m]范围内的深度，并将 $C_{d}epth$中深度的网格设置为1m。
上图（上）描绘了立体深度网络 (SDN) 管道。至关重要的是，所有卷积运算都专门在$C_{depth}$上进行。
下图比较了使用视差成本量（即 PSMNet）和深度成本量（SDN）的绝对深度估计误差的中值。

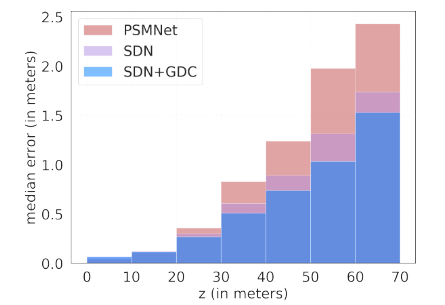
正如预期的那样，对于远距离深度，SDN 导致误差大大减小，并且在非常近的范围内仅略有增加（基于视差的方法过度优化）。

深度校正

SDN 显着改进了深度估计并更精确地渲染了对象轮廓（见下图）。

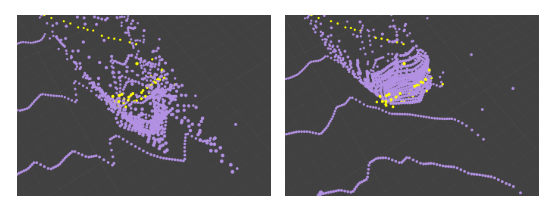
视差 cost volume（左）与深度 cost volume（右）。该图显示了从 LiDAR（黄色）和立体（紫色）获得的 3D 点，对应于 KITTI 中的一辆汽车，从鸟瞰图（BEV）看到的。差异 cost volume 中的点被拉长且嘈杂；而来自深度 cost volume 的点则忠实地捕捉到汽车轮廓。

然而，由于像素的离散性质，立体图像存在一个基本限制：视差（即相应像素之间水平坐标的差异）必须在单个像素的级别上进行量化，而深度是连续的。尽管可以通过更高分辨率的图像来减轻量化误差，但计算深度预测成本会随着分辨率的增加而呈三次方变化，从而突破了自动驾驶汽车中 GPU 的极限。

因此，论文探索了一种混合方法，利用具有极其稀疏（例如 4 束）但精确的深度测量的廉价 LiDAR 来纠正这种偏差。我们注意到，此类传感器太稀疏，无法捕获物体形状，并且不能单独用于检测。然而，通过将激光雷达点投影到图像平面上，我们可以获得一小部分“地标”像素的精确深度。

论文提出了一种基于图的深度校正（G??DC）算法，该算法有效地结合了渲染对象形状的密集立体深度和稀疏的精确激光雷达测量。从概念上讲，我们期望校正后的深度图具有以下属性：全局上，与 LiDAR 点关联的地标像素应具有精确的深度；在本地，应保留由相邻 3D 点捕获的、从输入深度图反投影的对象形状（参见公式 1）。

输入匹配

通过立体深度估计将来自 LiDAR (L) 和 Pseudo-LiDAR (PL) 的两个点云作为输入。后者是通过将深度为 $z$ 的像素 $(u,v)$ 转换为 3D 点 $(x_u,y_v,z)$ 来获得的。
首先，通过 PL 点云中的有向 K-最近邻 (KNN) 图（使用加速 KD 树）来表征局部形状，该图将每个 3D 点与其具有适当权重的 KNN 连接起来。同样，可以将 3D LiDAR 点投影到像素位置 $(u,v)$ 上，并将它们与相应的 3D 立体点进行匹配。不失一般性，假设我们获得了前 $n$ 个点的“地面实况”LiDAR 深度，而其余 $m$ 点则没有地面实况。我们将 3D 立体深度估计称为 $Z\in {\mathbb{R}}^{n+m}$，将 LiDAR 深度地面实况称为 $G\in {\mathbb{R}}^n$。

边权重

为了构建 3D 的 KNN 图，忽略前 $n$ 个点的 LiDAR 信息，只使用它们在 $Z$ 中预测的立体深度。让 ${\mathcal{N}}_i$ 表示第 $i$ 个点的 $k$ 个邻居的集合。此外，令 $W\in {\mathbb{R}}^{(n+m)\times (n+m)}$ 表示权重矩阵，其中 $W_{ij}$ 表示点 $i$ 和 $j$ 之间的边权重。受到流形学习先前工作的启发，选择权重作为系数，从 ${\mathcal{N}}_i$ 中任何点的邻居深度重建任何点的深度。可以通过以下约束二次优化问题来求解这些权重：
$$W={\text{arg?min}}_W||Z?WZ|{|}_2^2,s.t.W1=1and{W}_{ij}=0\text{if}j\notin {\mathcal{N}}_i.\text{\hspace{1em}(7)}$$

这里 $1\in {\mathbb{R}}^{n+m}$表示全1向量。只要我们选择 $k>3$ 并且点处于一般位置，就有无限多个满足 $Z=WZ$ 的解，并且论文选择具有最小 L2 范数的解（通过轻微的 L2 正则化获得）。

深度校正

将校正后的深度值表示为 $Z^{{}^{\prime }}\in {\mathbb{R}}^{n+m}$，其中 $Z^{{}^{\prime }}=[Z_L^{{}^{\prime }};Z_{PL}^{{}^{\prime }}]$ 和 $Z_L^{{}^{\prime }}\in {\mathbb{R}}^n$ 和 $Z_{PL}^{{}^{\prime }}\in {\mathbb{R}}^m$ ，其中 $Z_L^{{}^{\prime }}\in {\mathbb{R}}^n$ 是具有 LiDAR 地面实况的点的深度值，否则为 $Z_{PL}^{{}^{\prime }}\in {\mathbb{R}}^n$ 。
对于 LiDAR 测量的 $n$ 个点，将深度更新为（地面实况）值 $Z_L^{{}^{\prime }}=G$ 。然后，在给定 $G$ 和 $W$ 中编码的加权 KNN 图的情况下求解 $Z_{PL}^{{}^{\prime }}$ 。具体来说，更新剩余深度 $Z_{PL}^{{}^{\prime }}$，使得任何点 $i$ 的深度仍然可以使用学习的权重 $W$ 以高保真度重建为其 KNN 深度的加权和；即，如果点 $i:1\le i\le n$ 移动到新的深度 $G_i$，则 ${\mathcal{N}}_i$ 中的邻居也必须进行校正，使得 $Gi\approx {\sum }_{j\in {\mathcal{N}}_i}{W}_{ij}{Z}_j^{{}^{\prime }}$。此外，必须纠正邻居的邻居，并且这几个 $n$ 点的深度会传播到整个图。我们可以通过另一个二次优化直接求解最终的 $Z^{{}^{\prime }}$：
$$Z^{{}^{\prime }}={\text{arg?min}}_{Z^{{}^{\prime }}}||Z^{{}^{\prime }}?W{Z}^{{}^{\prime }}|{|}^2,s.t.Z_{1:n}^{{}^{\prime }}=G\text{\hspace{1em}(8)}$$

为了说明校正过程，想象一下最简单的情况，其中仅单个点（$n=1$）的深度更新为 $G_1=Z_1+\delta$。方程 8 的新最佳深度是类似地移动所有剩余点，即 $Z^{{}^{\prime }}=Z+1\delta$：由于 $Z=WZ$ 且 $W1=1$，必须有 $W(Z+1\delta )=Z+1\delta$。

在 $n>1$ 的设置中，最小二乘损失确保不同 LiDAR 深度估计之间的软扩散。方程 7 和方程 8 中的两个优化问题都可以使用稀疏矩阵求解器准确有效地求解。

从基于图的流形学习的角度来看，GDC 算法让人想起局部线性嵌入，并用地标来指导最终解决方案。图 1 生动地说明了如何使用一些稀疏 LiDAR 测量值（黄色）来校正 KITTI 数据集中汽车的 SDN（紫色）的初始 3D 点云。得到的点（蓝色）位于地面实况框内，清楚地显示汽车的轮廓。图 4 显示了 GDC（蓝色）相对于纯 SDN 深度估计的额外改进。误差（仅在非地标像素上计算）在整个图像上进行校正，其中许多区域没有 LiDAR 测量。这是因为伪 LiDAR 点云足够密集，并且我们选择足够大的 $k$（实际上，我们使用 k = 10），这样 KNN 图通常是连通的（或由几个大的连通分量组成）。对于汽车等物体，GDC 的改进要明显得多，因为这些物体通常会被四个 LiDAR 光束接触，并且可以得到有效校正。

结论

在论文中，做出了两项贡献，以改进自动驾驶车辆中的 3D 物体检测，而无需昂贵的 LiDAR。
首先，将视差估计确定为基于立体的系统的主要误差源，并提出了一种直接端到端学习深度的新方法，而不是通过视差估计。其次，主张不要使用昂贵的激光雷达传感器来了解物体的局部结构和深度。相反，人们可以使用商品立体相机来实现前者，并使用廉价的稀疏激光雷达来纠正所得深度估计中的系统偏差。提供了一种新颖的图传播算法，该算法集成了两种数据模态，并使用两个稀疏矩阵求解器传播稀疏但准确的深度估计。由此产生的系统 PSEUDO-LIDAR ++ (SDN + GDC) 的性能几乎与 75,000 美元的 64 光束 LiDAR 系统相当，但只需要 4 个光束和两个商用相机，总成本不到 1,000 美元。

，，，