有序矩阵中第 K 小的元素

题目链接

有序矩阵中第 K 小的元素

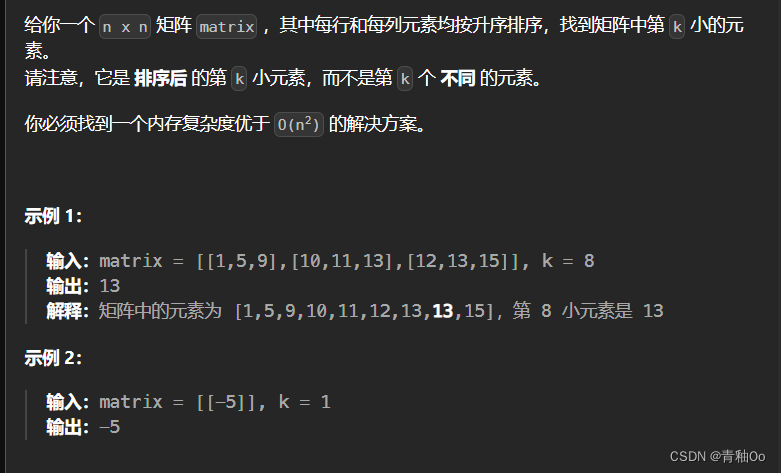
题目描述

注意点

• 每行和每列元素均按升序排序
• 找到一个内存复杂度优于 O(n2) 的解决方案

解答思路

• 使用二分查找，思路为：
  （1）因为左上角的元素值更小，右下角的元素值更大，先将left设置为左上角元素的值，right设置为右下角元素的值；
  （2）判断不大于left和right中间值mid的元素数量sum；
  （3）如果sum小于k，则将left设置为mid + 1，否则将right设置为mid。
• 不断重复上述过程，直到满足sum等于k时right的最小值，此时left等于right，且right是大于等于矩阵中K个元素的临界点，所以矩阵中一定会有一个元素等于right（否则说明并没有找到sum等于k时right的最小值），right也就是有序矩阵中第 K 小的元素

代码

class Solution {
    int n;
    public int kthSmallest(int[][] matrix, int k) {
        n = matrix.length;
        int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + (right - left) / 2;
            int sum = countLessThanMid(matrix, mid);
            if (sum < k) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }

    public int countLessThanMid(int[][] matrix, int mid) {
        int sum = 0;
        for (int i = 0; i < n; i++) {
            // 如果左上角都大于mid，则一定没有小于等于mid的元素存在
            if (matrix[i][0] > mid) {
                return sum;
            }
            // 如果右上角都小于等于mid，则该行所有元素都小于等于mid
            if (matrix[i][n - 1] <= mid) {
                sum += n;
                continue;
            }
            // 其余情况查找改行小于等于mid的元素
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] > mid) {
                    break;
                }
                sum++;
            }
        }
        return sum;
    }
}

关键点

• 二分查找的思路
• 怎么找到sum等于k时right的最小值
• 当right - left=1，且两个数都是负数的时候，求mid时会等于right的值，此时如果sum >= k，则会一直卡在循环中无法跳出，需要保证这种特殊情况求mid也是left，所以求mid时使用left + (right - left) / 2